加农炮 [Pick's Theorem][Farey Sequence][Stern-Brocot Tree][类欧]

Link
No Response

---

Pick’s Theorem
Reference

---

Farey Sequence
F n = { a / b    ∣    ( a , b ) = 1    ,    0 ≤ a , b ≤ n } F_n=\{a/b\;|\;(a,b)=1\;,\;0\le a,b\le n\} Fn​={a/b∣(a,b)=1,0≤a,b≤n} 元素从小到大排列。
性质1 除 $F_1$ 外的任意阶 Farey Sequence 都有奇数个元素，且位于中间的数是 $1/2$
性质2 $F_n$ 关于中点对称的两项和为 $1$
[Important]性质3 $F_n[x]=a/b,F_n[x+1]=c/d,$ 则 $bc-ad=1$
*性质 Farey Sequence 中的数都是真分数。（无视 $1/0$）

显然地： $F_n$ 的大小是 $2^n+1$ （如果算上 $1/0$ ）。

---

Stern-Brocot Tree
定义我就不讲啦。

从 $F_1$ 开始每次把相较上一阶 Farey Sequence 多出的数作为上一阶比上上阶多出的数的子结点，
且相对位置不变，就能构造出 Stern-Brocot Tree 。

这么讲可能有点啰嗦，简略讲就是：
在上面每两个相邻真分数 $x_1/y_1,x_2/y_2$ 中间插入 $(x_1+x_2)/(y_1+y_2)$ 就能构成下一层
（以上也适用于 farey sequence
然后把下一层的每个数跟上一层生成它的连边。

实际上， Farey Sequence 是 Stern-Brocot Tree 的衍生。
无视 $0/1$ 和 $1/0$ ，Stern-Brocot Tree就是一棵满的完全二叉树。

---

类欧
$$f(a,b,c,n)=\sum _{i=0}^n\lfloor \frac{ai+b}{c}\rfloor$$
$$g(a,b,c,n)=\sum _{i=0}^n\lfloor \frac{ai+b}{c}\cdot i\rfloor$$
$$h(a,b,c,n)=\sum _{i=0}^n{\lfloor \frac{ai+b}{c}\rfloor }^2$$

---

推f
$a\ge corb\ge c$ ， $f(a,b,c,n)=\lfloor \frac{a}{c}\rfloor \cdot \frac{n(n+1)}{2}+\lfloor \frac{b}{c}\rfloor \cdot (n+1)+f(a\%c,b\%c,c,n)$
$otherwise,f(a,b,c,n)=nm-f(c,c-b-1,a,m-1)$
具体过程
推的时候注意一些细节，比如小于等于变成小于的时间啦/之类的

---

推g
$a\ge corb\ge c$ ， $g(a,b,c,n)=\lfloor \frac{a}{c}\rfloor \cdot \frac{n(n+1)(2n+1)}{6}+\lfloor \frac{b}{c}\rfloor \cdot \frac{n(n+1)}{2}+g(a\%c,b\%c,c,n)$
$otherwise,$
$\begin{array}{rcl}g(a,b,c,n)& =& \sum _{i=0}^n\lfloor \frac{ai+b}{c}\cdot i\rfloor \\ & =& \sum _{i=0}^{n}i\sum _{j=0}^{m-1}[j+1\le \frac{ai+b}{c}]\\ & =& \sum _{i=0}^{n}i\sum _{j=0}^{m-1}[\frac{cj+c-b-1}{a}<i]\end{array}$
考虑对于每个 $j$ ，在各个 $i$ 处的取值组成一个等差数列。
$a_1=\lfloor \frac{cj+c-b-1}{a}\rfloor +1,a_{n-\lfloor \frac{cj+c-b-1}{a}\rfloor }=n$
等差数列求和 $\frac{(a_1+a_n)\cdot n}{2}$
$\begin{array}{rcl}g(a,b,c,n)& =& \frac{1}{2}\sum _{j=0}^{m-1}\left(\lfloor \frac{cj+c-b-1}{a}\rfloor +1+n\right)\left(n-\lfloor \frac{cj+c-b-1}{a}\rfloor \right)\\ & =& \frac{1}{2}\sum _{j=0}^{m-1}n(n+1)-\lfloor \frac{cj+c-b-1}{a}\rfloor -{\lfloor \frac{cj+c-b-1}{a}\rfloor }^2\\ & =& \frac{1}{2}\cdot n(n+1)m-f(c,c-b-1,a,m-1)-h(c,c-b-1,a,m-1)\end{array}$
震惊 g要先推h

---

推h
$a\ge corb\ge c,$
$\begin{array}{rcl}h(a,b,c,n)& =& h(a\%c,b\%c,c,n)+\frac{n(n+1)(2n+1)}{6}\cdot {\lfloor \frac{a}{c}\rfloor }^2+(n+1)\cdot {\lfloor \frac{b}{c}\rfloor }^2\\ & & \\ & & +2\lfloor \frac{b}{c}\rfloor f(a\%c,b\%c,c,n)+\lfloor \frac{a}{c}\rfloor \lfloor \frac{b}{c}\rfloor n(n+1)\end{array}$
$otherwise,$
$\begin{array}{rcl}h(a,b,c,n)& =& \sum _{i=0}^n{\lfloor \frac{ai+b}{c}\rfloor }^2\\ & =& \sum _{i=0}^n\sum \end{array}$
啊？
考虑怎么把 ${\lfloor \frac{ai+b}{c}\rfloor }^2$ 拆出来。
$x^2=2\cdot \frac{x(x+1)}{2}-x=\left(2\sum _{i=1}^{x}i\right)-n$

$\begin{array}{rcl}h(a,b,c,n)& =& \left[2\sum _{i=0}^n\left(\sum _{j=1}^{\lfloor \frac{ai+b}{c}\rfloor }j\right)\right]-\lfloor \frac{ai+b}{c}\rfloor \\ & =& \left(2\sum _{i=0}^n\sum _{j=1}^{\lfloor \frac{ai+b}{c}\rfloor }j\right)-\sum _{i=0}^n\lfloor \frac{ai+b}{c}\rfloor \\ & =& \left(2\sum _{i=0}^n\sum _{j=1}^{m}j\cdot \left[j\le \lfloor \frac{ai+b}{c}\rfloor \right]\right)-f(a,b,c,n)\\ & =& \left[2\sum _{i=0}^n\sum _{j=0}^{m-1}(j+1)\cdot \left[\frac{cj+c-b-1}{a}<i\right]\right]-f(a,b,c,n)\\ & =& \left[2\sum _{j=0}^{m-1}(j+1)\left(n-\lfloor \frac{cj+c-b-1}{a}\rfloor \right)\right]-f(a,b,c,n)\\ & =& \left[2\sum _{j=0}^{m-1}(j+1)n-(j+1)\lfloor \frac{cj+c-b-1}{a}\rfloor \right]-f(a,b,c,n)\\ & =& m(m+1)n-2g(c,c-b-1,a,m-1)-2f(c,c-b-1,a,m-1)-f(a,b,c,n)\end{array}$

---

回归正题，，，
很显然，如果人够多，所有目标都会被打掉。
我们暂且把整个坐标系往左下移动一格。
打到某一个目标 $(x,y)$ 的话，旋转的角度是 $\arctan (x/y)$
也就是说每一个真分数 $x/y$ （$0\le x<n,0\le y<m$ ， 包括 $1/0$ 和 $0/1$） 对应一条射线的目标
并且这条射线的斜率是 $x/y$ 。
构造 Farey Sequence 就可以得到（按照射线的）炮击顺序。

一条射线上有多少目标呢？相当于求射线 $j=xi/y$ 上的整点数目（不包含原点）。
为了方便显然可以特判掉 $x=0$ 和 $y=0$ 的情况。剩下的怎么求呢
显然是 min ⁡ { n x , m y } \min\{\frac{n}{x},\frac{m}{y}\} min{xn​,ym​}
。。。

剩下的问题就是 你看看这个数据范围
是不是有、大啊
至少对于每组询问要做到 $O(\log )$ 或者 $O(\mathrm{sqrt})$ 之类的
直接暴力预处理构造 Farey Sequence / Stern-Brocot Tree 都不现实。。

性质 Stern-Brocot Tree 上，分母为 $n$ 的真分数到根节点的路径上的拐点数目不超过 $\log n$ 个
证明只需要考虑一个不停拐啊拐的路径 然后考虑利用 $\frac{a+b}{c+d}$ 构造下一层的那个性质
而如果直接走下来的话，最多可能要走 $O(n)$

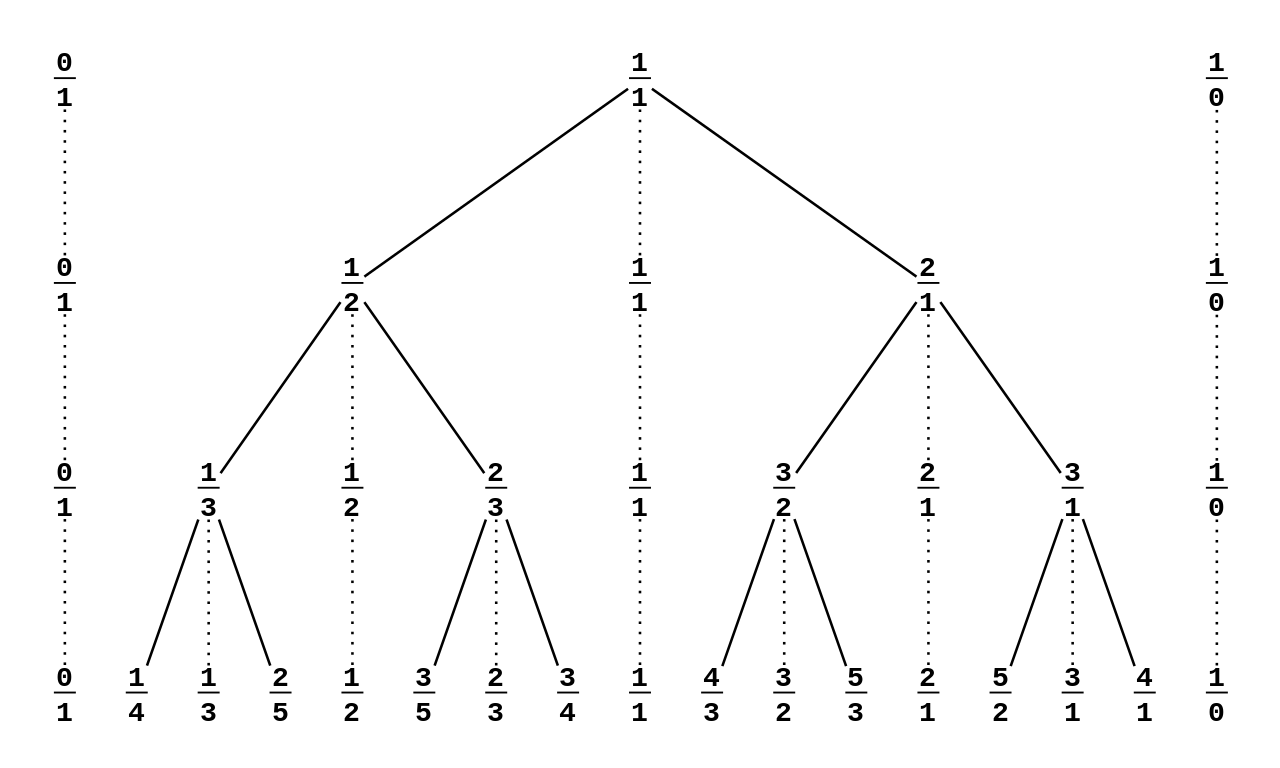
给出一张 Stern-Brocot Tree 的图方便观察（）图引 Wikipedia

这样的话在 Stern-Brocot Tree 上走路的时候拐点是 $O(\log n)$ 的
在每个拐点处搞倍增。然后就变成了 $O({\log }^{2}n)$
注意到我们只需要求出第 $k$ 个人能够打到哪里，所以每组询问走一次即可。
但是二分的话前面的问题就变成了求射线某一边的整点数目。。用类欧判定，喜加一个 $\log$
$O(T{\log }^{3}n)$ 。

倍增杀了我
鸽了啊