动态规划2：不同路径、不同路径||、整数拆分、不同的二叉搜索树、第2节总结

6. 不同路径

例题62：
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

数论

从（0,0）走到（m-1,n-1）一共向下m-1次，向右n-1次
也就是说一共走走m+n-2步
即给m+n-2个不同的数，随便取m-1个数，有几种取法？
也就是一共走m+n-2步，在其中选取m-1个位置向下，其余向右。
那就是一个组合问题：

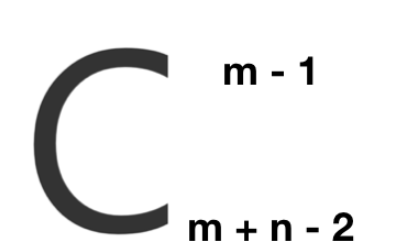
**如果组合直接求分子分母的话，两个int相乘会溢出！**所有不能把分子、分母都算出再做除法。在算分子的时候就要不断除以分母，代码如下：

时间复杂度O(m)，空间复杂度O(1)
class Solution {
public int uniquePaths(int m, int n) {
        long long numerator = 1; // 分子
        int denominator = m - 1; // 分母
        int count = m - 1;
        int t = m + n - 2;
        while (count--) {
            numerator *= (t--);
            while (denominator != 0 && numerator % denominator == 0) {//如果分子能整除分母，就先除掉
                numerator /= denominator;//分子分母相除后再乘以下一次，不会溢出
                denominator--;
            }
        }
        return numerator;
    }
};

动态规划

1. 确定dp
2. 数组的含义与下标
   dp[i][j]表示从（0,0）位置到（i,j）位置的路径条数。
3. 确定递推公式
   dp[i][j]可以从dp[i][j-1]向右走一格，或从dp[i-1][j]向下走一格。
   因此，dp[i][j]=dp[i-1][j]+dp[i][j-1]
4. 初始化
   dp[0][0]=0，因为机器人就是从0,0开始
   dp[i][0]=1，dp[0][j]=0，因为向下向右的路只有一条。
5. 确定遍历方向
   因为dp[i][j]是由左方的dp[i][j-1]和上方的dp[i-1][j]推导而来的，那么每一层从左到右依次遍历即可。
6. 举例推导递推公式。m=3,n=2
   dp[2][1]=dp[2][0]+dp[1][1]=dp[1][0]+dp[1][0]+dp[0][1]=3。递推公式得到的值与实际值相符。
   代码如下：

时间复杂度O(m*n)，空间复杂度O(m*n)
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp=new int[m][n];
        for(int i=0;i<m;i++) dp[i][0]=1;
        for(int j=0;j<n;j++) dp[0][j]=1;
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

7. 不同路径||

例题63：
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

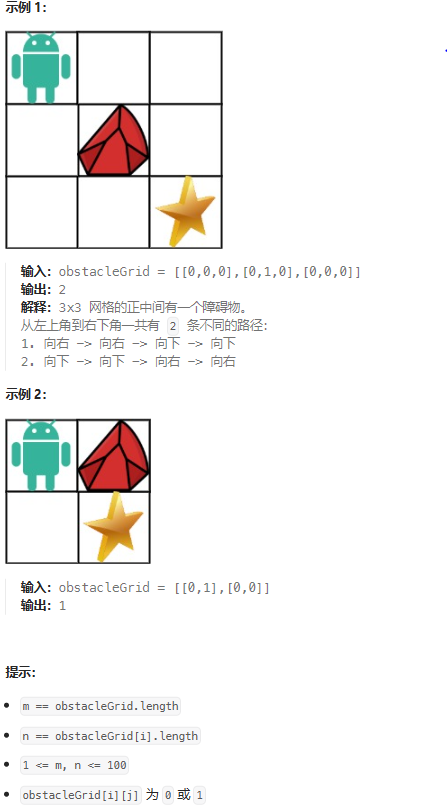
和上一题类似，不过有障碍物的位置dp[i][j]=0。并且第一行和第一列如果某个位置有障碍物，之后的dp全为0。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m=obstacleGrid.length;
        int n=obstacleGrid[0].length;
        int[][] dp=new int[m][n];//初始化为0
        int i=0;
        while(i<m){
            if(obstacleGrid[i][0]!=1){
            dp[i][0]=1;
            i++;
            }
            else
            break;//如果碰到障碍物，之后保持初始化值0
        }

            int j=0;
        while(j<n){
            if(obstacleGrid[0][j]!=1){
            dp[0][j]=1;
            j++;
            }
            else
            break;
        }

            for(i=1;i<m;i++){
                for(j=1;j<n;j++){
                    if(obstacleGrid[i][j]!=1)
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
            }
            return dp[m-1][n-1];
    }
}

8. 整数拆分

例题343：
给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

动态规划

1. 确定dp数组和下标含义
   dp[i]就是数字i的最大乘积
2. 确定递推公式
   dp[i]是由从i/2到i-1的最大值*（i-该数）的最大值决定的
   dp[i]=max(max(dp[i-1],i-1)*1,max(dp[i-2],i-2)*2…max(dp[i/2],i/2)*i/2)
3. 初始化
   dp[1]=1,dp[2]=1
4. 遍历方向
   从前向后
5. 举例验证递推公式
   dp[3]=max(dp[2],2)*1,max(dp[1]*2))=2，与实际相符。
   代码如下：

时间复杂度O(n^2)，空间复杂度O(n）
lass Solution {
    public int integerBreak(int n) {
        int[] dp=new int[n+1];
        dp[1]=1;
        dp[2]=1;
        for(int i=3;i<=n;i++){
            for(int j=i/2;j<i;j++){
                 dp[i]=Math.max(Math.max(dp[j],j)*(i-j),dp[i]);
            }
        }
        return dp[n];
    }
}

9. 不同的二叉搜索树

例题96：
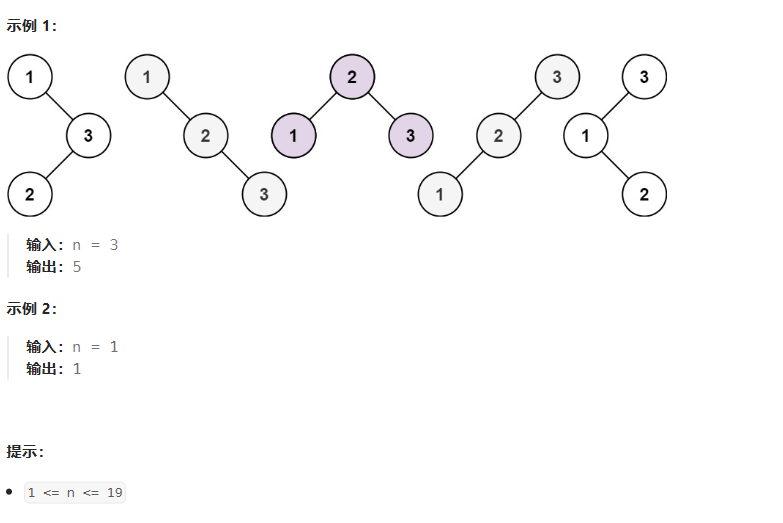
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

动态规划

1. 确定dp数组和下标
   dp[i]表示整数i的二叉搜索树最大种类。
2. 确定递推公式
   由测试用例可得到，dp[3]=5
   当头节点为1时，其右子树有两个节点，其分布格局与n=2时相同。
   当头节点为3时，其左子树有两个节点，其分布格局与n=2时相同。
   当头节点为2时，其左右子树各有一个节点，其分布于n=1时相同。
   所以dp[i]可以由dp[i-1]与dp[i-2]推出。

即dp[3]=头节点为1的二叉搜索树+头节点为2的二叉搜索树+头节点为3的二叉搜索树

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

所以，dp[i]=dp[i-1]*dp[1]+dp[i-2]*dp[2]+…+dp[2]*dp[i-2]+dp[1]*dp[i-1]

dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]

j相当于是头结点的元素，从1遍历到i为止。
dp[i]+=dp[i-j]*dp[j-1]

3. 初始化
   dp[0]=1;从结果反推，如果得到dp[2]就需要dp[0]=1
   dp[1]=1;
   不初始化dp[2]是因为如果n=1，new的dp是长度2的数组，那么dp[2]就有运行时的下标溢出异常。
4. 遍历方向
   从1到i依次遍历
5. 举例证明递推公式
   i=3时，上述已经证明。
   代码如下：

时间复杂度为O(n^2)，空间复杂度为O(n）
class Solution {
    public int numTrees(int n) {
        int[] dp=new int[n+1];
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i]+=dp[i-j]*dp[j-1];
            }
        }
        return dp[n];
    }
}

这道题难度较大，递推公式需要画图分析，并且很难想清楚头节点下的布局和上一个数的分布相同。并且该数的二叉搜索树个数与之前所有头节点的个数相关从此基础上推导。

10. 第二节动规总结

1. 不同路径：首先要想清楚dp[i][j]的含义，并且想清楚dp[i][j]可以由左节点和上节点得到。
2. 不同路径||：中间有障碍的dp为0，第一列和第一行一旦出现障碍，其后都为0。
3. 整数拆分：想清楚dp[i]是由i/2到i-1区间内的dp和i的最大值*（i-该数）得到，最好用例子推演。
4. 不同的二叉搜索树：这道题较难，需要画图推算，并且很难想到每一个节点下的布局是上一个节点布局，且总个数是左右子树布局的乘积。