机器学习的神经网络是以人脑中的神经网络为启发的,历史上出现过很多不同的版本,其中最著名也是最常用的算法就是本篇要讲的在1980提出的backpropagation(反向传播),它被应用于多层向前神经网络。下面先来讲一下多层向前神经网络,也可以称为BP神经网络。
多层向前神经网络由3部分组成,输入层(input layer),隐藏层(hidden layers),输出层(output layers),如下图

输入层和输出层都只有1层,隐藏层可以有N层,每一层由若干个节点单元组成。上图的神经网络是一个两层的神经网络,输入层不算在内。
将实例特征向量传入输入层,经过隐藏层,一系列的计算,最终可以得到输出层的结果。输入层后面的每一层可以通过上一层的加权求和再进行非线性方程转化得到。
这个加权求和是怎么做的呢?我们可以看到前一层与后一层单元之间有一些连线,每一条连线就对应一个权重,将前一层的单元与对应 的权重相乘再相加,最后进行非线性方程转化就能得到后一层每个单元的值。每一层的输出是下一层的输入。
因为加权求和之后以后计算的方程是非线性的,所以理论上讲有一个很强大的功能,只要训练集足够大,隐藏层足够多,可以用神经网络模拟出任何方程。90年代这个算法被人应用,但是当时大家觉得它的功能并不是很强大,那是因为当时的计算能力不高,一旦神经网络的层数多于3层,训练的时间就会非常长,效果也不好,而且因为互联网不普及数据集也很有限,所以神经网络的这个算法并不是一个很强的算法,当时站在巅峰的是SVM支持向量机。但是今天随着计算能力的大大增强以及数据集增大,神经网络为前身延伸出了的强大的深度学习,深度学习的强大就在于数据集和计算能力大大增强的情况下可以用更多的隐藏层模拟出更多的方程。
使用神经网络训练数据之前,必须先设计神经网络的结构,也就是确定神经网络的层数以及每层的单元个数。
先来看输入层单元的问题。
首先有一个问题特征向量传入输入层 之前必须要先标准化到0,1之间,目的是加速学习的过程。
另外,变量的类型既可以是离散型变量,也可以是连续型变量。
比如离散型变量的可以被编码,用几个单元分类别对应一个特征值可能被赋的值。举个例子:
特征值A可能取3个值(a0, a1, a2),可以用三个输入单元来表示A,假如A是a0, 三个单元是1,0,0, A是a1,三个单元是0,1,0。这样进行编码。所以并不一定说输入层每一个单元对应特征向量的每一个特征值。
再来看输出层的问题
神经网络既可以用来做分类(classification)问题,也可以解决回归(regression)问题。回归问题与分类问题最大的区别就是它要预测的值不是像分类这样的离散值,而是连续型变量。
神经网络主要解决的是还是分类问题,对于分类问题,假如只有两类那么可以用1个输出单元表示,(分别用0,1表示两类),如果大于两类,那么有几类就用几个输出单元就行了。
对于隐藏层,目前没有一个明确的规则来确定到底有几层,一般是先确定一个层数,根据实验测试和误差,以及准确度来实验,慢慢改进。
对于准确度怎么来算呢?前面几篇实践中的做法都是把一组数据分成训练集和测试集两部分。训练集来训练模型。测试集输入进去看结果是不是对的,根据正确率得到一个准确度。
不过机器学习中有一种更常用和科学的方法,交叉验证方法(cross-validation)。下面来介绍一下这种方法。如下图。

前面我们用的方法是把数据分成2份,一份测试集一份数据集。交叉验证方法就是把数据分成更多份,比如10份,9份训练1份测试得到一个准确度。这样10份中每一份都当一次测试集,其它9份当训练集,继续下去可以得到10个准确度,做一个均值就得到最终的准确度。这就是交叉验证方法,这样可以更充分的利用数据集。这个10份只是举个例子,实际上可以分成任意的K份,所以这个方法也被称为K-fold cross validation。
这样就简单讲了多层向前神经网络这个结构,下面介绍应用在上面的backpropagation算法。
1.backpropagation算法通过迭代性处理训练集中的实例,也就是说需要一波一波的将训练集喂的输入层中。
2.通过对比神经网络后输入层预测值(predicted value)与真实值(target value)之间的差距,反方向(从输出层=>隐藏层=>输入层)倒推回来,通过一定的法则,方程,以最小化误差为目标更新每个连接的权重Wij以及每个单元的偏向b。这样就完成了一轮先正方向输入得到结果,再比对结果倒推修正网络的过程,这样一轮一轮的将训练集喂到神经网络模型中,最终就能得到一个训练好的神经网络。
对于最开始的权重和偏向可以随机的赋一个(-1,1)或者(-0.5, 0.5)之间的值
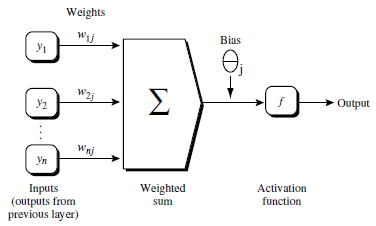
如上图所示n个单元,加权求和加上一个偏向后得到一个值,再代入非线性转化方程方程

得到输出结果。
这个非线性的方程是一个sigmoid函数。
通过这样的方式就能够一步一步正向的计算出最后输出,那么怎么倒推回去修正优化神经网络呢?
是利用误差来反向传送,先来看一下误差的计算方式:
对于输出层,假设单元的真实值是T,已经得到单元的预测值为P,那么误差 E =P*(1-P)*(T-P)
对于隐藏层误差计算稍有不同,设当前单元的值是P,前一层的误差已经计算出了为E1,那么当前误差 E = P*(1-P)*∑E1*W , 这里的E1和W指的是对应的前一层一组误差和权重,对应的相乘求和。
得到了误差怎么来更新权重和偏向呢?
这里是用梯度爬行的方法来更新权重和偏向。
权重更新:
更新量 Δw = L*E*P
W = w+Δw
这里W是更新后的权重,w是原权重,Δw是更新量,E是当前单元算出的误差,P是当前单元值, L是学习率。
学习率L是个0到1之间的数,就好比是逼近目的地的步伐的步长,是我们手动设置的一个值,学习率越大,跨度越大,但是可能跨过目的地,越小越精细但可能就需要很多很多步。所以比较好的方式是开始的时候L比较大,越靠近目的地L越小,我们可以设置一个比率根据每一轮的结束让L有一个从大到小的渐变。
偏向更新:
Δb = L*E
B = b + Δb
这样就完成了反向权重与偏向的更新。
一轮一轮的训练,终止条件是什么呢?
我们可以设置多种方式,比如权重的更新低于某个阈值,预测的错误率低于某个阈值,或者达到预设一定的循环次数来终止。
这样,根据一个神经网络模型,一组训练集数据,还有学习率L,通过上述的方法一轮轮的训练最终就可以得到一个训练好的神经网络。训练好的神经网络的每条线上都有一个好的权重,每个单元都有一个好的偏向。
下面举一个简单例子,一个2层神经网络完成一轮的计算过程。
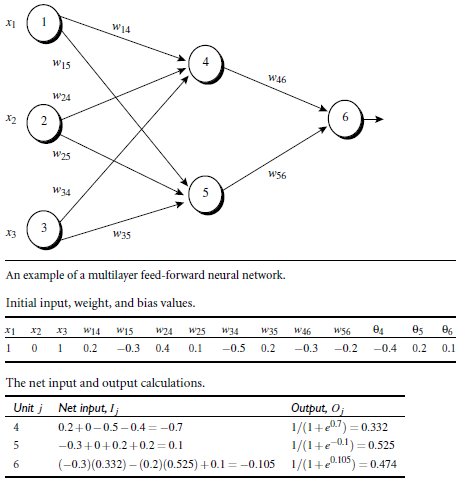
如上图,假设输入层1,2,3输入数据1,0,1 ,初始化的权重和偏向都已经随机的给出,则正向计算,单元4,5,6先加权求和,再代入非线性方程转化的过程结果都已给出。
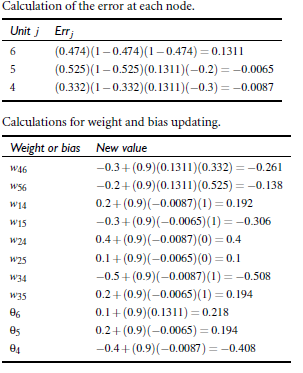
那么反向更新呢,代入公式,从后往前求出6,5,4的误差,在将其代入权重偏向更新公式,这里选取学习率为0.9, 计算过程如下图
这样就完成了一轮的计算。








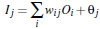














 5301
5301

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








