队列的顺序存储结构之循环队列

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。
队列是一种先进先出（First In First Out）的线性表，简称FIFO.允许插入的一端称为队尾，允许删除的一端称为队头。
队列的顺序存储结构使用数组的实现，假设数组长度为N，这时删除队头元素的时候，这个元素后面的每一个元素都要移动，这样就会出队的性能会下降。如下图所示：

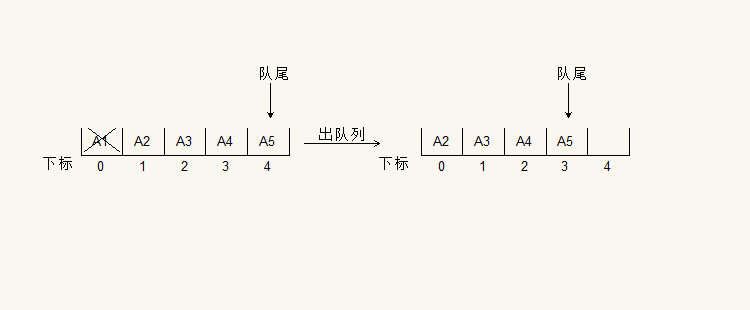
删除队首的元素A1，那么后面的其他元素都要移动到这个位置，这样会造成出队性能下降。
现在假设我们删除了之后队列中的其余元素位置不变，是不是就可以解决了这个问题。
那样是可以，但是又会引发新的问题，
现在队列中有5个元素已经满了，让A1,A2,A3都出队，这个时候会空出3个位置，如下图

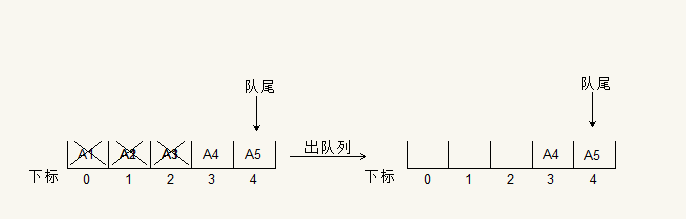
这个时候我们同样也是不可以在入队了，然而队列中还是有空间的，我们想要使用这个剩余空间，这个时候我们是要在下标为0的位置放置元素，这样数组的空间就可以充分利用。这样这个数组就相当于一个头尾相接的循环。我们把这种头尾相接的的顺序存储结构称为循环队列。相当于下图

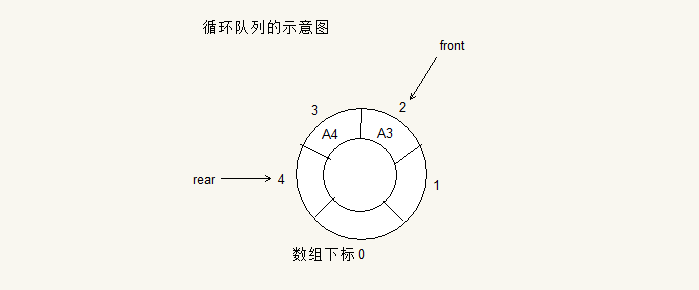
当下标为4的位置有元素，在想添加元素的时候，就放到下标为0的位置。
队列引入了两个指针front,rear.
front指针指向队头的元素，rear指针指向队尾元素的下一个位置。
比如上图中 A3是队首元素 所以front指向它，A4是队尾元素，所以rear指向它下一个位置。
假设队列的长度为QueueSize,
那么front和rear下一个位置的下标的分别为 (front+1)%QueueSize ,(rear+1)%QueueSize;
队列的长度的计算公式为: (rear-front+QueueSize)%QueueSize;
队列为空的条件 ：front ==rear
队列满时的条件： (rear+1)%QueueSize == front
下面是使用代码演示循环队列的用法：

#include <stdio.h>
#define MAX_SIZE 5

typedef struct Queue
{
    int data[MAX_SIZE];
    int front;
    int rear;
}QUEUE,*PQUEUE;

void initQueue(PQUEUE);//循环队列初始化
bool addQueue(PQUEUE,int);//循环队列添加
bool deleteQueue(PQUEUE,int*);//循环队列删除
bool isFull(PQUEUE);//循环队列是否已满
bool isEmpty(PQUEUE);//循环队列是否为空
void showQueue(PQUEUE);//打印
int main(void)
{
    QUEUE Queue;
    int pVal;
    initQueue(&Queue);
    addQueue(&Queue,30);
    addQueue(&Queue,60);
    addQueue(&Queue,100);
    showQueue(&Queue);
    if(deleteQueue(&Queue,&pVal))
    printf("删除的元素是： %d\n",pVal);
    addQueue(&Queue,-100);
    addQueue(&Queue,-900);
    showQueue(&Queue);
    return 0;
}

void showQueue(PQUEUE p)
{
    int front = p->front;
    int rear = p->rear;
    while((front)%MAX_SIZE!=rear)
    {
        printf("%d  ",p->data[front]);
        front = (front+1)%MAX_SIZE;
    }
    printf("\n");

}

bool isFull(PQUEUE p)
{
    if((p->rear+1)%MAX_SIZE==p->front)
    {
        return true;
    }
    return false;
}
bool isEmpty(PQUEUE p)
{
    if(p->rear==p->front)
    {
        return true;
    }
    return false;
}


void initQueue(PQUEUE q)
{
    q->front = 0;
    q->rear = 0;
}

bool addQueue(PQUEUE p,int e)
{
    if(isFull(p))
    {
        return false;
    }
    p->data[p->rear] = e;
    p->rear = (p->rear+1)%MAX_SIZE;//下标移动到下一个位置
    return true;
}

bool deleteQueue(PQUEUE p,int * pVal)
{
    if(isEmpty(p))
    {
        return false;
    }
    *pVal = p->data[p->front];
    p->front=(p->front+1)%MAX_SIZE;
    return true;
}