51Nod-1201-整数划分

ACM模版

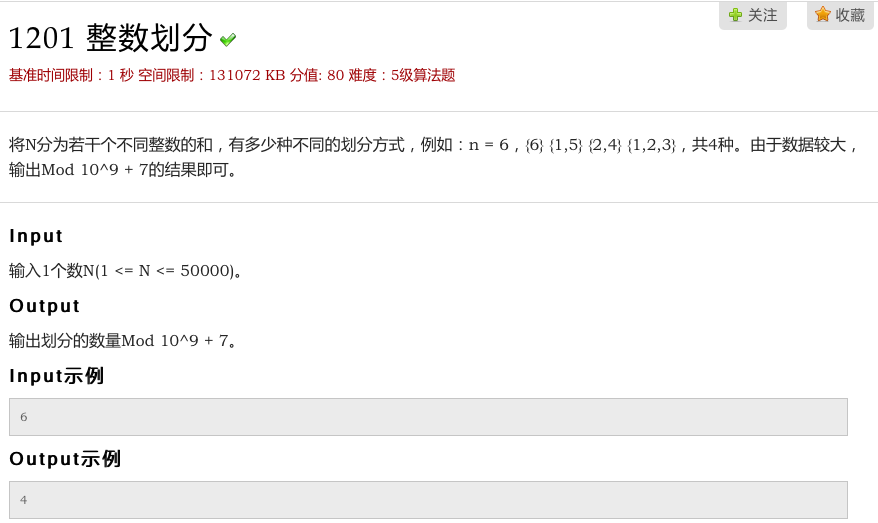
描述

题解

相关讨论区给的思路解决了我的疑惑，十分好的一道题，dp[i][j]表示由i个数字组成j的种类，状态转移方程为：

dp[i][j] = dp[i - 1][j - i] + dp[i][j - i]

因为N最大为5w，所以可以求出i的上限在320左右，定义一个int dp[350][50000]大小的还是可以的，但是我想玩得花一些，于是用的滚动数组，然而却忽略了将dp[i][0]~dp[i][(i + 1) * i / 2 - 1]全部置为0，或者说直接对dp[i]初始化为0。

        for (int j = 0; j < (i + 1) * i / 2; j++)
        {
            dp[i & 1][j] = 0;
        }

代码

#include <iostream>

using namespace std;

const int MAXN = 5e4 + 10;
const int MOD = 1e9 + 7;

int dp[2][MAXN];

int main(int argc, const char * argv[])
{
    int N;
    cin >> N;

    long long res = 1;
    for (int i = 1; i <= N; i++)
    {
        dp[1][i] = 1;
    }
    for (int i = 2; (i + 1) * i / 2 <= N; i++)
    {
        for (int j = 0; j < (i + 1) * i / 2; j++)
        {
            dp[i & 1][j] = 0;
        }
        for (int j = i; j <= N; j++)
        {
            dp[i & 1][j] = (dp[(i - 1) & 1][j - i] + dp[i & 1][j - i]) % MOD;
        }
        res = (res + dp[i & 1][N]) % MOD;
    }
    std::cout << res << '\n';

    return 0;
}