HDU-1198-Farm Irrigation

ACM模版

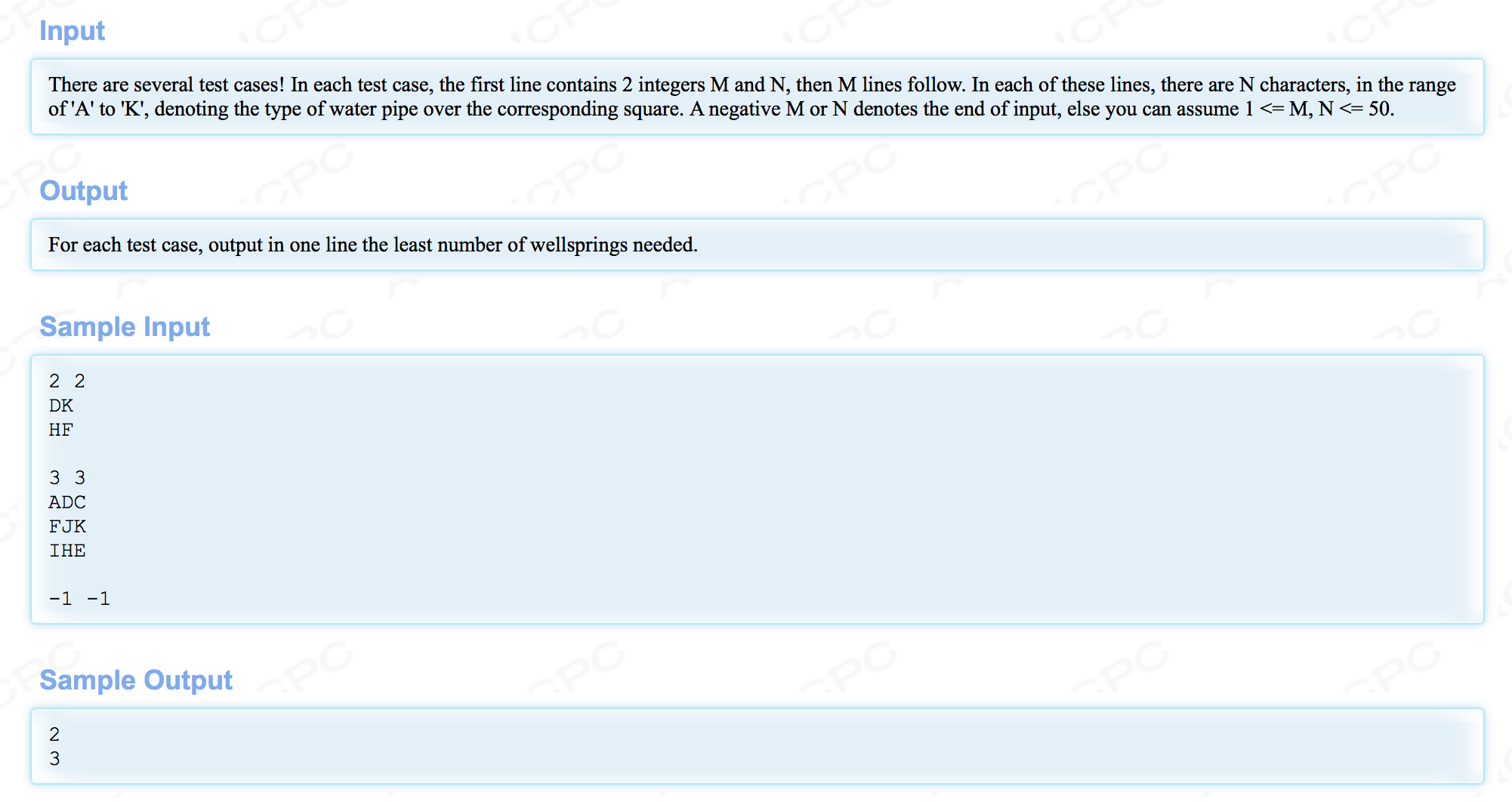
描述

题解

使用二进制标记匹配状态，并查集搞搞，思路倒是不难，并查集的改造需要注意细节~~~

还可以DFS搞。

代码

#include <iostream>
#include <cstdio>
#include <cstring>

#define mem(a, b) memset(a, b, sizeof(a))

using namespace std;

//  二进制表示状态
const int map[] = {3, 6, 9, 12, 10, 5, 7, 11, 13, 14, 15};
//  只用考虑两个方向衔接
const int dir[2][2] = {{0, 1}, {1, 0}};

const int MAXN = 555;

int flag;
int maxRoom;
int M, N;
int pre[MAXN * MAXN];
char farm[MAXN][MAXN];
int root;

int find(int x)
{
    int r = x;
    while (pre[r] != r)
    {
        r = pre[r];
    }

    int i = x, j;
    while (i != r)
    {
        j = pre[i];
        pre[i] = r;
        i = j;
    }
    return r;
}

void join(int x, int y)
{
    int flag = 1;   //  表示衔接方向，0为上下衔接，1为左右衔接
    for (int i = 0; i < 2; i++)
    {
        int x_ = x + dir[i][0];
        int y_ = y + dir[i][1];
        if (y_ > M)
        {
            flag = 0;
            continue;
        }
        if (x_ > N)
        {
            break;
        }

        //  转成状态
        int posA = farm[x][y] - 'A';
        int posB = farm[x_][y_] - 'A';

        int state = 0;  //  标记是否连通
        if (flag)
        {
            if (((map[posA] >> 2) & 1) && (map[posB] & 1))
            {
                state = 1;
            }
            flag = 0;
        }
        else
        {
            if ((map[posA] >> 3) & 1 && ((map[posB] >> 1) & 1))
            {
                state = 1;
            }
        }

        if (state)
        {
            int fx = find((x - 1) * M + y);
            int fy = find((x_ - 1) * M + y_);
            if (fx != fy)
            {
                pre[fx] = fy;
                root--;
            }
        }
    }

    return ;
}

int main(int argc, const char * argv[])
{
    while (cin >> N >> M, N != -1 || M != -1)
    {
        root = N * M;

        for (int i = 0; i <= root; i++)
        {
            pre[i] = i;
        }

        for (int i = 1; i <= N; i++)
        {
            scanf("%s", farm[i] + 1);
        }

        for (int i = 1; i <= N; i++)
        {
            for (int j = 1; j <= M; j++)
            {
                join(i, j);
            }
        }

        cout << root << '\n';
    }

    return 0;
}