HDU-1245-Saving James Bond

ACM模版

描述

题解

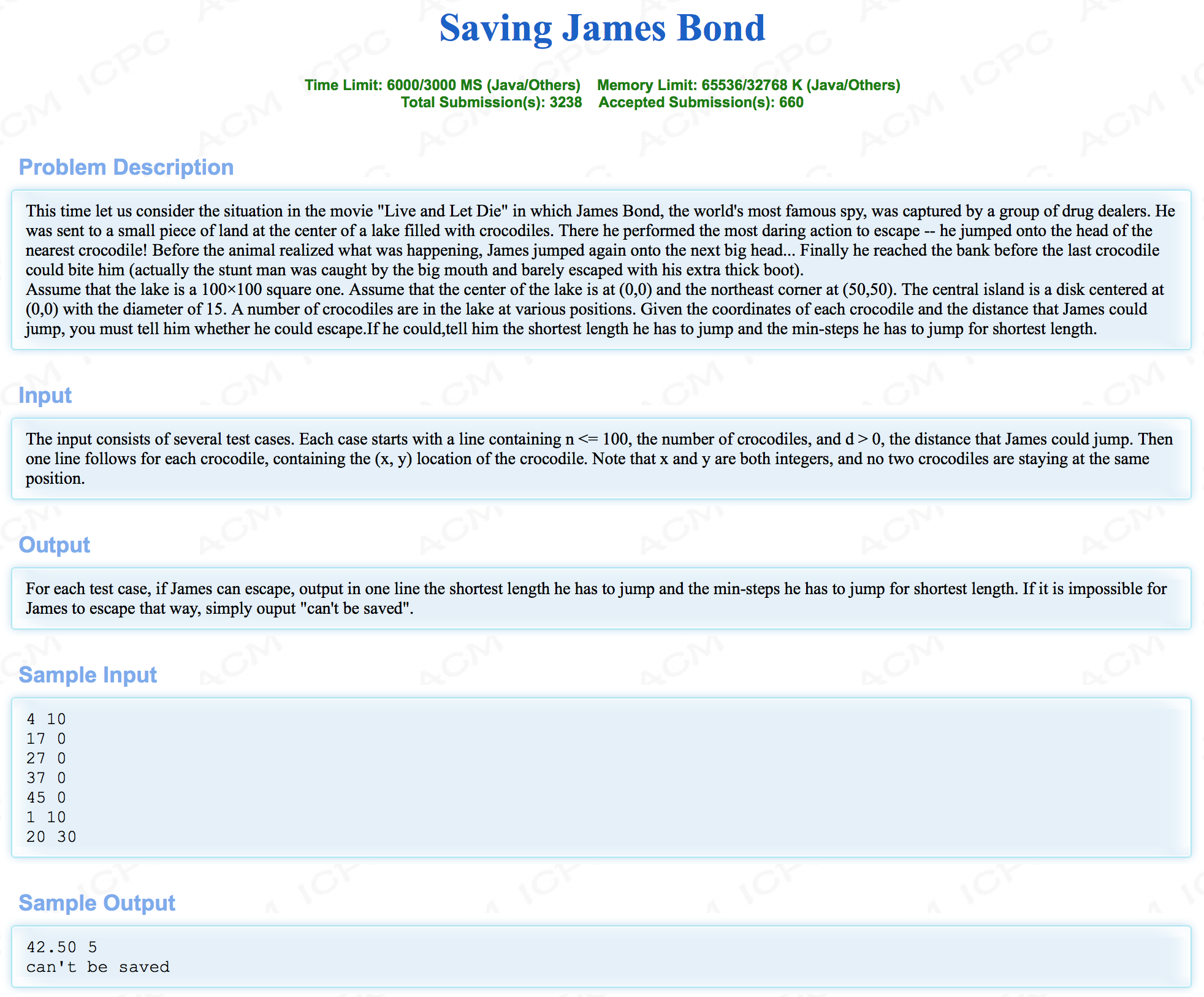
给定一个100X100的池子，中间(0, 0)处有一个直径为15的岛，然后湖中有许多踏点，问能否踩着踏点蹦跶出来，当然，有一个最远的蹦跶的距离d。

思路很清晰，最短路，只要求出两两点之间的距离加以处理，然后把岛当做源点，湖外当做终点，添加与其他点对应的路径信息即可，这里有一个问题是，精度十分高，并且数据强度十分高，也就是说，当路径长度一样时，要求输出的第二个步数要尽量小，那么也就是模板中的双路径信息的代码了，第一信息是路径距离，第二信息步数，每跳一步，lowsteps[]加一。

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>

using namespace std;

const int MAXN = 110;

struct cro
{
    int x;
    int y;
};

struct cro Cro[MAXN];

/*
 *  单源最短路径，Dijkstra算法，邻接矩阵形式，复杂度为O(n^2)
 *  求出源beg到所有点的最短路径，传入图的顶点数和邻接矩阵cost[][]
 *  返回各点的最短路径lowcost[]，路径pre[]，pre[i]记录beg到i路径上的父节点，pre[beg] = -1
 *  可更改路径权类型，但是权值必须为非负，下标0~n-1
 */
const int INF = 0x3f3f3f3f; //  表示无穷

double lowdis[MAXN];
int lowsteps[MAXN];
int visit[MAXN];
double map[MAXN][MAXN];

void dijkstra(int st, int n)
{
    int temp = 0;
    for (int i = 1; i <= n; i++)
    {
        lowdis[i] = map[st][i];
        lowsteps[i] = 1;
    }
    memset(visit, 0, sizeof(visit));

    visit[st] = 1;
    for (int i = 1; i < n; i++)
    {
        double MIN = INF;
        for (int j = 1; j <= n; j++)
        {
            if (!visit[j] && lowdis[j] < MIN)
            {
                temp = j;
                MIN = lowdis[j];
            }
        }
        visit[temp] = 1;
        for (int j = 1; j <= n; j++)
        {
            if (!visit[j] && map[temp][j] < INF)
            {
                if (lowdis[j] > lowdis[temp] + map[temp][j])
                {
                    lowdis[j] = lowdis[temp] + map[temp][j];
                    lowsteps[j] = lowsteps[temp] + 1;
                }
                else if (lowdis[j] == lowdis[temp] + map[temp][j])
                {
                    if (lowsteps[j] > lowsteps[temp] + 1)
                    {
                        lowsteps[j] = lowsteps[temp] + 1;
                    }
                }
            }
        }
    }

    return ;
}

//  两点间
double getDis(struct cro a, struct cro b)
{
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

//  点到边
double getDis_(struct cro c)
{
    double x = fabs(c.x);
    double y = fabs(c.y);
    double dis = 50 - x;
    dis = 50 - y > dis ? dis : 50 - y;
    return dis;
}

int main(int argc, const char * argv[])
{
    int n;
    double d;
    Cro[0].x = Cro[0].y = 0;

    while (cin >> n >> d)
    {
        //  特判
        if (n == 0)
        {
            if (d >= 42.50)
            {
                printf("42.50 1\n");
            }
            else
            {
                printf("can't be saved\n");
            }
            continue;
        }

        for (int i = 0; i <= MAXN; i++)
        {
            for (int j = 0; j <= MAXN; j++)
            {
                map[i][j] = INF;
            }
        }

        for (int i = 1; i <= n; i++)
        {
            scanf("%d%d", &Cro[i].x, &Cro[i].y);
            for (int j = 1; j < i; j++)
            {
                double dis = getDis(Cro[i], Cro[j]);
                if (dis <= d)
                {
                    map[i][j] = map[j][i] = dis;
                }
            }
        }

        //  特判
        if (d >= 42.50)
        {
            printf("42.50 1\n");
            continue;
        }

        //  岛到cro的距离\cro到湖外距离
        for (int i = 1; i <= n; i++)
        {
            double dis = getDis(Cro[0], Cro[i]) - 7.50;
            if (dis <= d)
            {
                map[i][0] = map[0][i] = dis;
            }
            dis = getDis_(Cro[i]);
            if (dis <= d)
            {
                map[i][n + 1] = map[n + 1][i] = dis;
            }
        }

        dijkstra(0, n + 2);

        if (lowdis[n + 1] == INF)
        {
            printf("can't be saved\n");
        }
        else
        {
            printf("%.2lf %d\n", lowdis[n + 1], lowsteps[n + 1]);
        }
    }

    return 0;
}

参考

《最短路》