NOIP 刷题记录

前言

$\mathcal{N}othingelse$

$\text{Partition Game}$

先考虑 dp。

设 $ls{t}_{a_i}$ 表示 $a_i$ 上一次出现的位置，$d{p}_{i,j}$ 表示前 $i$ 个数分 $j$ 段的最小代价和，就有：

d p i , j = min ⁡ 0 < k ≤ i { d p k − 1 , j − 1 + v a l ( k , i ) } dp_{i,j} = \min_{0 < k \le i} \{ dp_{k - 1,j - 1} + val(k, i)\} dpi,j​=0<k≤imin​{dpk−1,j−1​+val(k,i)}

其中 $val(k,i)$ 就表示从第 $k$ 个到第 $i$ 个的代价，有：

$$val(k,i)=\{\begin{array}{ll}0& ls{t}_{a_i}<k\\ i-ls{t}_{a_i}& ls{t}_{a_i}\ge k\end{array}$$

如果对 $val$ 进行初始化，按上述转移的复杂度应该是 $O(n^{2}k)$。考虑优化，观察到转移方程的前一部分 $d{p}_{k-1,j-1}$ 恒定，后半部分如果值改变，改变就为 $i-ls{t}_{a_i}$。于是考虑线段树进行区间加，区间最小值优化。先以第 $j-1$ 层的 $d{p}_{k,j-1}$ 为底建立线段树，再在枚举 $i$ 时加上 $a_i$，询问最小值为 $d{p}_i$。

内层的时间复杂度就变成了$\log$ 级，总时间复杂度 $O(n\log nk)$，还可继续优化空间复杂度，缩掉 $j$ 的一层。

$\text{Alyona and towers}$

很明显的数据结构题， 需支持区间加及最长单峰长度查询。

考虑线段树维护。分析一下答案的情况。

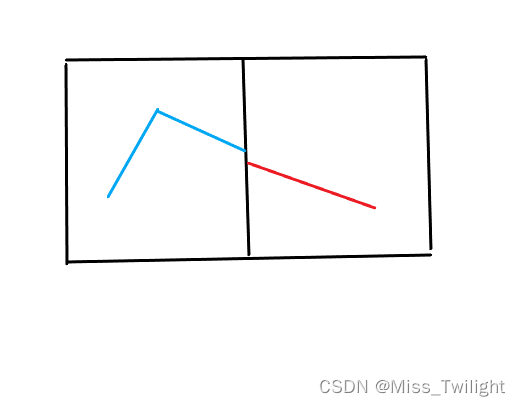
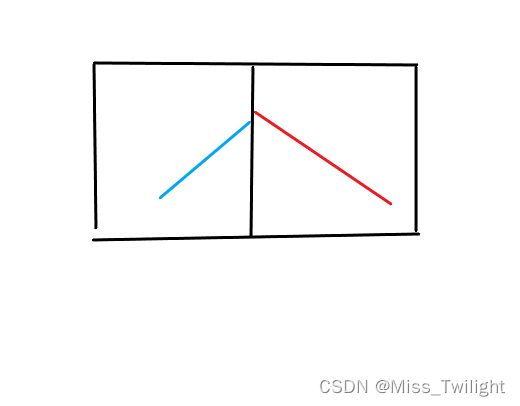
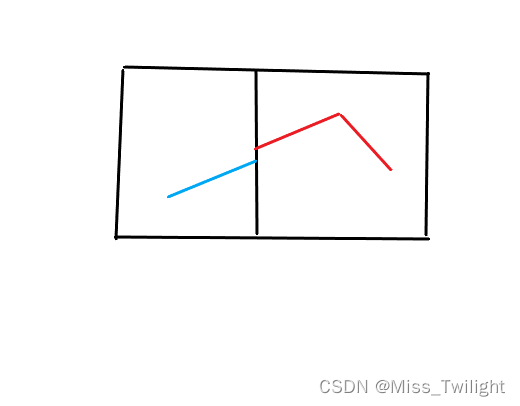
答案的分布就有几种情况：

• 左/右区间的答案
• 峰值在左区间
• 峰值恰好在左右端点的交接处
• 峰值在右区间

那就考虑线段树端点维护下列的信息：
1.左、右端点的值
2.在右端点结束的最长连续单增序列长度
3.从左端点开始的最长连续单减序列长度
4.在右端点结束的最长单峰序列长度
5.从左端点开始的最长单峰序列长度
6.区间答案，懒标

根据答案的分布情况，在上传时分别讨论维护即可，细节可能较多。

$\text{Danger of Mad Snakes}$

先考虑直接计算每一只蛇的贡献，发现由于答案中平方的存在，导致需要计算类似 $a_i{a}_j$ 之类的项，单独处理一只蛇的贡献并不好求。于是考虑计算每一对蛇的贡献。

对于每一对蛇，它们共同的贡献即为它们被共同选中的次数，设 $a$ 为选中第一只蛇的次数， $b$ 为选中第二只蛇的次数，$c$ 为同时选中两只蛇的次数，它们的贡献就是 $2a_i{a}_j（C_n^m-C_{n-a}^m-C_{n-b}^m+C_{n-a-b+c}^m）$。

然后答案还需加上相同的 $a_i$ 的平方，数量即为能选到此蛇的次数。

统计能选到的次数时可以考虑二位前缀和。

$\text{Complicated Computations}$

求一个数列的所有子区间的 $mex$ 值的 $mex$

看到 $mex$ 的第一反应就是莫队，于是考虑一下莫队。在判断一个数 $a_i$ 是否可能成为 $mex$ 时，因为如果一个区间存在这个数，这个数不可能成立为 $mex$，可以考虑在每一个 $a_i$ 的位置分段，在每相邻两个 $a_i$ 之间求 $mex$，如图：

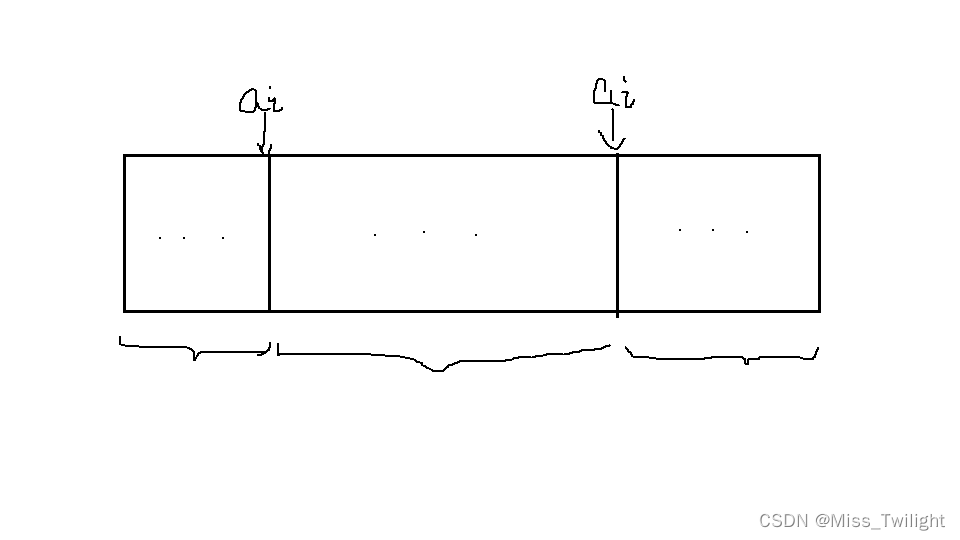
先将所有要询问的区间处理出来，然后对所有区间跑莫队维护。跑答案则从小到大枚举，这个数如果没有区间的 $mex$ 是它自己，就是答案。

有一个显然的优化，加入每两个 $a_i$ 之间的查询时，判断区间长度是否够，不够就不用考虑。不优化的时间复杂度也是对的，最多有 $n$ 组相邻的 $a_i$，区间数量是 $n$ 的级别。总时间复杂度 $O(n\sqrt{n})$

$\text{Mr. Kitayuta’s Colorful Graph}$

膜拜神仙根号

有一道弱化版 $\text{CF505B}$，可以先把它过掉。

考虑解决弱化版的两种方法：

• 将每个颜色的边分开存下来，分别考虑每个颜色建立并查集。暴力枚举每个并查集内部的点对，判断操作询问中是否有此点对。
• 将每个颜色的边分开存下来，分别考虑每个颜色建立并查集。枚举所有询问，判断操作询问中的点对是否联通。

对于第一种方法，所有颜色的边数小于 $\sqrt{m}$ 的点对总数，复杂度是 $O(m\sqrt{m}\alpha (n))$。

对于第二种方法，所有边数大于 $\sqrt{m}$ 的颜色不会超过 $\sqrt{m}$ 个，结合内部枚举所有询问的 $O(q)$，总时间复杂度 $(q\sqrt{m}\alpha (n))$

于是以 $\sqrt{m}$ 为界，分别处理，总时间复杂度 $(m\sqrt{m}\alpha (n))$

$\text{Till I Collapse}$

再次膜拜神仙根号

考虑根号分治。在 $k$ 较小部分时可以直接暴力求解。在 $k$ 较大部分时，显然答案的段数小于等于 $\lceil \frac{n}{k}\rceil$ ，然后我们对于每个不同的答案，很容易发现答案具有单调性，二分出它对应的答案区间，在判断下一个答案。

假设分界点为 $P$，暴力求解的时间复杂度为 $O(nP)$ ，二分时因为答案的段数小于等于 $\lceil \frac{n}{k}\rceil$，所以时间复杂度为 $O(n\log n\lceil \frac{n}{P}\rceil )$， $P$ 取 $\sqrt{n}$ 能过，但想求最优就考虑均值：

$$nP+n\log n\frac{n}{P}\ge 2\sqrt{n^3\log n}=2n\sqrt{n\log n}$$$$\therefore nP\ge n\sqrt{n\log n}⟹P\ge \sqrt{n\log n}$$

当 $P$ 取 $\sqrt{n\log n}$ 时最优，总时间复杂度为 $2n\sqrt{n\log n}$

$\text{Hossam and (sub-)palindromic tree}$

想成树形 dp 就跑远了，比如我

在序列上应该是很好想的，考虑区间 dp，设 $d{p}_{l,r}$ 表示 $l$ 到 $r$ 的最长回文子序列，转移也很好写：

$$d{p}_{l,r}=\max (d{p}_{l+1,r},d{p}_{l,r+1},d{p}_{l+1,r-1}+2\ast [s_l==s_r])$$

考虑将其转移到树上，思想和在序列上操作是差不多的，只不过情况复杂一些。设树上节点 $u$，$v$， $u$ 的深度小于 $v$ 的深度，其最近公共祖先为 $lc{a}_{u,v}$，那么

• 当 $u=lc{a}_{u,v}$ 时：
  $$d{p}_{u,v}=\max (d{p}_{so{n}_u,v},d{p}_{u,f{a}_v},d{p}_{so{n}_u,f{a}_v}+2\ast [s_u==s_v])(lc{a}_{so{n}_u,f{a}_v}=so{n}_u)$$

• 当 $u\ne lc{a}_{u,v}$ 时：
  $$d{p}_{u,v}=\max (d{p}_{f{a}_u,v},d{p}_{u,f{a}_v},d{p}_{f{a}_u,f{a}_v}+2\ast [s_u==s_v])$$

实现上，可以记忆化搜索由长序列向短序列推，边界为只剩 1 或 2 个点时判一下即可。总时间复杂度 $O(n^2)$

$\text{Karen and Supermarket}$

想到树形 dp 就跑远了对了 。

在每一个 $x_i$ 与 $i$ 之间连边，设 $d{p}_{i,j,0/1}$ 为在 $i$ 的子树中选 $j$ 个物品，（不）使用优惠券的最小代价。则有：
{ d p u , j + k , 0 = min ⁡ { d p u , j , 0 + d p v , k , 0 } d p u , j + k , 1 = min ⁡ { d p u , j , 1 + min ⁡ ( d p v , k , 0 , d p v , k , 1 ) } \begin{cases} dp_{u,j+k,0} = \min\{dp_{u,j,0} + dp_{v,k,0}\} \\ dp_{u,j+k,1} = \min\{dp_{u,j,1}+\min(dp_{v,k,0}, dp_{v,k,1}) \} \end{cases} {dpu,j+k,0​=min{dpu,j,0​+dpv,k,0​}dpu,j+k,1​=min{dpu,j,1​+min(dpv,k,0​,dpv,k,1​)}​

$j$ 需要倒序枚举，保证答案更新先后。直接暴力背包的时间复杂度为 $O(n^3)$，需要记录 $u$ 的子树中的节点个数，枚举子树时不断更新，优化上下界，时间复杂度为 $O(n^2)$

$\text{Makoto and a Blackboard}$

先考虑暴力如何实现。

设 $d{p}_{i,j}$ 为将正整数 $i$ 进行 $j$ 次操作后的期望值，若 $i=\prod b^p$ ，其中 $b$ 为质数，则有：
$$d{p}_{i,j}=\frac{1}{\prod p}\sum d{p}_{\frac{i}{x},j-1}(x\mid i)$$

不容易发现，这是一个积性函数。

对于 $i$ 的每一个质因数 $b$，每一次变换它的指数 $p$ 就会等概率变成 $[0,p]$ 中的一个数，而这种变换不受其他质因数影响，每次减少指数的概率对于每个质因数来说互相独立，可以推导出为积性函数。

于是对每个质因数分别讨论，设 $f_{i,j}$ 表示一个质数的 $i$ 次方经过 $j$ 次操作后的结果，于是有：

$$f_{i,j}=\frac{1}{i+1}\sum _{x=0}^i{f}_{x,j-1}$$

$$d{p}_{i,j}=\prod f_{b,p,k}$$

实现可以考虑质因数分解后求值，记忆化搜索。

$\text{列队}$

考虑动态开点的平衡树，对于每一行建一颗平衡树，节点维护一段区间，如果查询节点在一段区间中，就把这段区间裂成两段。

观察到每一次操作，对于其他无关的行，前 $m-1$ 列的数值是不会变的，只有第 $m$ 列可能改变，于是单独维护第 $m$ 列的信息，建一颗树，于是有 $n+1$ 棵平衡树。

对于 $y=m$ 的操作，只用分裂第 $n+1$ 棵线段树，将第 $x$ 个节点拎到最后。

对于 $y\ne m$ 的操作，先分裂出第 $x$ 棵树的第 $y$ 个节点 $a$ ，再分裂出第 $n+1$ 棵树的第 $x$ 个节点 $b$，将 $a$ 挂在第 $n+1$ 棵树最后，将 $b$ 挂在第 $x$ 棵树的最后。