快速判断点在三角形内

△ABC，点P （向量a，b，c，p）

收集了一些算法：

1. 叉乘法

   原理：

   沿 △ABC 各有向边按一定方向走（顺时针或逆时针），判断点 P 是否在该边的某侧（右侧或左侧），若点 P 在三条边的同侧，则点 P 在 △ABC 内。

   实现：

   分别计算向量 AB、BC、CA 与向量 AP、BP、CP 的向量积（叉乘），若三个结果均同号（正或负，为零表示 P 在边上），则可得点 P 在 △ABC 内。

   该算法只需要做 3 次叉乘（6 次普通数值乘法），效率高，且没有浮点误差。
   

2. 面积法

   原理：

   若点 P 在 △ABC 内，则 △ABP、△BCP、△CAP 的面积之和应等于 △ABC 的面积。

   实现：

   利用两个向量叉积的几何意义为该两个向量所围三角形面积的 2 倍，分别计算 AB×BP、BC×CP、CA×AP、AB×BC，若 |AB×BP| + |BC×CP| + |CA×AP| = |AB×BC|，则得点 P 在 △ABC 内。

   这个算法用得比较普遍，需要做 4 次叉乘（8 次普通数值乘法），效率和叉乘法差不多，同时避免了使用海伦公式（）

点评：

1.差乘法比面积法稍微高效一点。在2D平面两个算法都有效。但是如果在3D空间。面积法仍可行，差乘法失效

2.矢量叉积：（矢量，右手螺旋定则）

1）2D平面
设矢量P = ( x1, y1 )，Q = ( x2, y2 )，则矢量叉积定义为由P，Q所定义的平行四边形的带符号的面积，即：P × Q = x1*y2 - x2*y1，其结果是一个标量。显然有性质 P × Q = - ( Q × P ) 和 P × ( - Q ) = - ( P × Q )。
叉积的一个非常重要性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系：
若 P × Q > 0 , 则P在Q的顺时针方向。
若 P × Q < 0 , 则P在Q的逆时针方向。
若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。
可以用来判断折线段的拐向判断，可用作多边形凹凸判定。

2）3D空间

设

=(

)，

=(

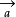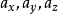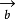)。 i， j， k分别是X，Y，Z轴方向的单位向量，则：

a×b= (

-

)

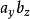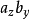i+(

-

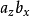) j+(

-

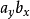) k，显然我们假设z轴分量为0，就退化到2D的情形a×b=

(

-

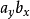) k

所以2D的情况下很容易求出由

，

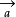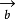定义的平行四边形的面积，即|

-

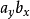|，但是如果3D情况，就需要平方再开方。计算复杂度提高，精度下降。

（精度下降会影响这里浮点数的判等么？其实如果是自己实现差乘，可以不开方，反正就是判断相等，但是一般来说会调用系统的接口吧，所以还是会开方的）

所以问题就来了在3D的情况下

（1）有没有更高效的算法判断点是否在三角形内部？

想法一：

既然要点在三角形内部，首先要满足点在三角形所在的平面，其次就是退化到2D的场景了。

那么如何判断点在三角形所在平面呢？

首先求出三角形所在平面的法向量（如AB×AC），然后判断法向量与PA或PB或PC是否垂直。实际就是求AB×AC和PA（或PB或PC）的点积是否为0.

（2）类似于2D平面多边形的凹凸判定。3D多面体的凹凸判定又如何呢？