一、插入排序
伪算法:
INSERTION-SORT(A)
1 for j=2 to A.length
2 key=A[j]
3 //Insert A[j] into the sorted sequence A[1..j-1]
4 i=j-1
5 while i>0 and A[i]>key
6 A[i+1]=A[i]
7 i=i-1
8 A[i+1]=key
下图是表明对A=<5,2,4,6,1,3>该算法的工作流程:
概念引入:循环不变式--->方便用来证明算法的正确性。
二、分治法
核心思想:递归求解;分解---->解决----->合并。
1.分治法用于排序
伪算法:
MERGE-SORT(A,p,r)
1 if p<r
2 q=[(p+r)/2]
3 MERGE-SORT(A,p,q)
4 MERGE-SORT(A,q+1,r)
5 MERGE(A,p,q,r)
其中使用的MERGE(A,p,q,r)就是将有序子数组L[p...q]和R[q+1...r]合并。注意下面的算法使用了“哨兵元素”来简化算法长度(不用每次判断某个子数组是否已经为空)
MERGE(A,p,q,r)
1 n1=q-p+1
2 n2=r-q
3 //let L[1...n1+1] and R[1...n2+1] be new arrarys
4 for i=1 to n1
5 L[i]=A[p+i-1]
6 for j=1 to n2
7 R[j]=A[q+j]
8 L[n1+1] = max
9 R[n2+1] = max
10 i=1,j=1
11 for k=p to r
12 if L[i]<=R[j]
13 A[k]=L[i]
14 i=i+1
15 else
16 A[k]=R[j]
17 j=j+1
斐波那契数:
F(0) = 0 , F(1) = 1
F(i) = F(i-1) + F(i-2)
2.分治法应用之----最大子数组问题
问题背景(抽象出来之后的):一组有正数,负数的数组。找出最大子数组:即一个元素连续的子数组,其元素之后最大。
例子如下:
问题分析:
假设我们要用分治法来求解最大子数组问题。使用递归的思路,对数组A[low...high]的求解就转化成对数组A[low...mid]和A[mid+1...high]的递归求解。但是我们要找的最大子数组除了可能完全在A[low...mid]中或者完全在A[mid+1...high],还有一种可能几十跨越了中点,即我们要找的A[i...j]满足:low<=i<=mid<j<=high。所以我们有三种情况:
(1)A[i...j]完全位于子数组A[low...mid]之中,递归求解
(2)A[i...j]完全位于子数组A[mid+1...high]之中,递归求解
(3)A[i...j]跨越了中点,此时A[i...j] = A[i...mid]+A[mid+1...j],这里的A[i...mid]+A[mid+1...j]现在可以在线性时间内求出。
图示:
首先给出上述情况三的求解伪算法:
FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)
1 left_sum = min ,max_feft = mid
2 sum=0
3 for i=mid downto low
4 sum+=A[i]
5 if sum>left_sum
6 left_sum=sum
7 max_left=i
8 right_sum = min ,max_right = mid+1
9 sum=0
10 for j=mid+1 to high
11 sum+=A[j]
12 if sum>right_sum
13 right_sum=sum
14 max_right=j
15 return (max_left,max_right,left_sum+right_sum)
现在给出基于递归处理和FIND-MAX-CROSSING-SUBARRAY来求解最大子数组的伪算法:
FIND-MAXIMUM-SUBARRAY(A,low,high)
1 if high == low
2 return (low,high,A[low])
3 else
4 mid=[(low+high)/2]
5 (left_low,left_high,left_sum) = FIND-MAXIMUM-SUBARRAY(A,low,mid)
6 (right_low,right_high,right_sum) = FIND-MAXIMUM-SUBARRAY(A,mid+1,high)
7 (cross_low,cross_high,cross_sum) = FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)
8 max_sum = max(left_sum,right_sum,cross_sum)
9 return (max_low,max_high,max_sum)
3.分治法应用之----矩阵乘法的Strassen算法
略
分治法时间复杂度的度量方法:
(1)用带入法求解递归式
(2)用递归树方法求解递归式
(3)用主方法求解递归式(主定理)
三、概率分析和随机算法








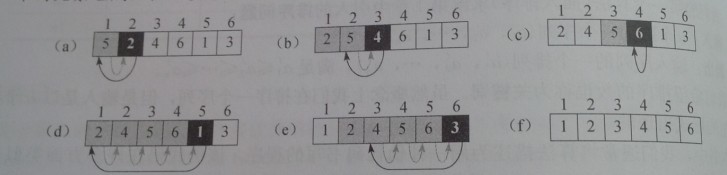



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








