迪菲-赫尔曼密钥交换

   迪菲－赫尔曼密钥交换（Diffie–Hellman key exchange，简称“D–H”） 是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道建立起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。
   迪菲－赫尔曼通过公共信道交换一个信息，就可以创建一个可以用于在公共信道上安全通信的共享秘密（shared secret）。

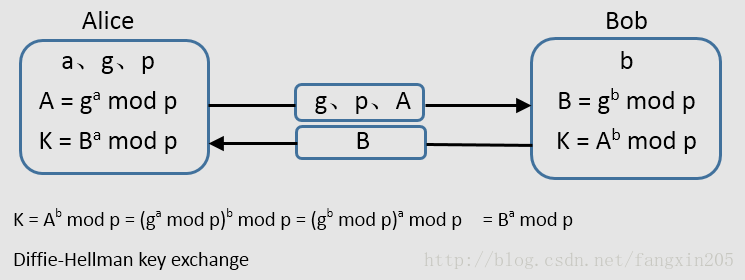
  交换信息的整个过程：

其中g、p、A、B是公开在网络中传输，a、b是秘密的。

    最早提出这个协议使用一个素数p的整数模n乘法群以及其原根g。下面展示这个算法，绿色表示非秘密信息，红色表示秘密信息。