从零开始学昇腾Ascend C算子开发-第四篇：常用算子实现

4.1 基础算子

4.1.1 元素级算子（Element-wise）

什么是元素级算子

元素级算子就是对输入张量的每个元素独立进行运算，元素之间没有依赖关系。这种算子最容易并行化，也最容易向量化。

常见的元素级算子有Add、Sub、Mul、Div这些算术运算，还有ReLU、Sigmoid这些激活函数。

Add算子实现

Add算子就是两个输入相加，输出对应位置的元素和。

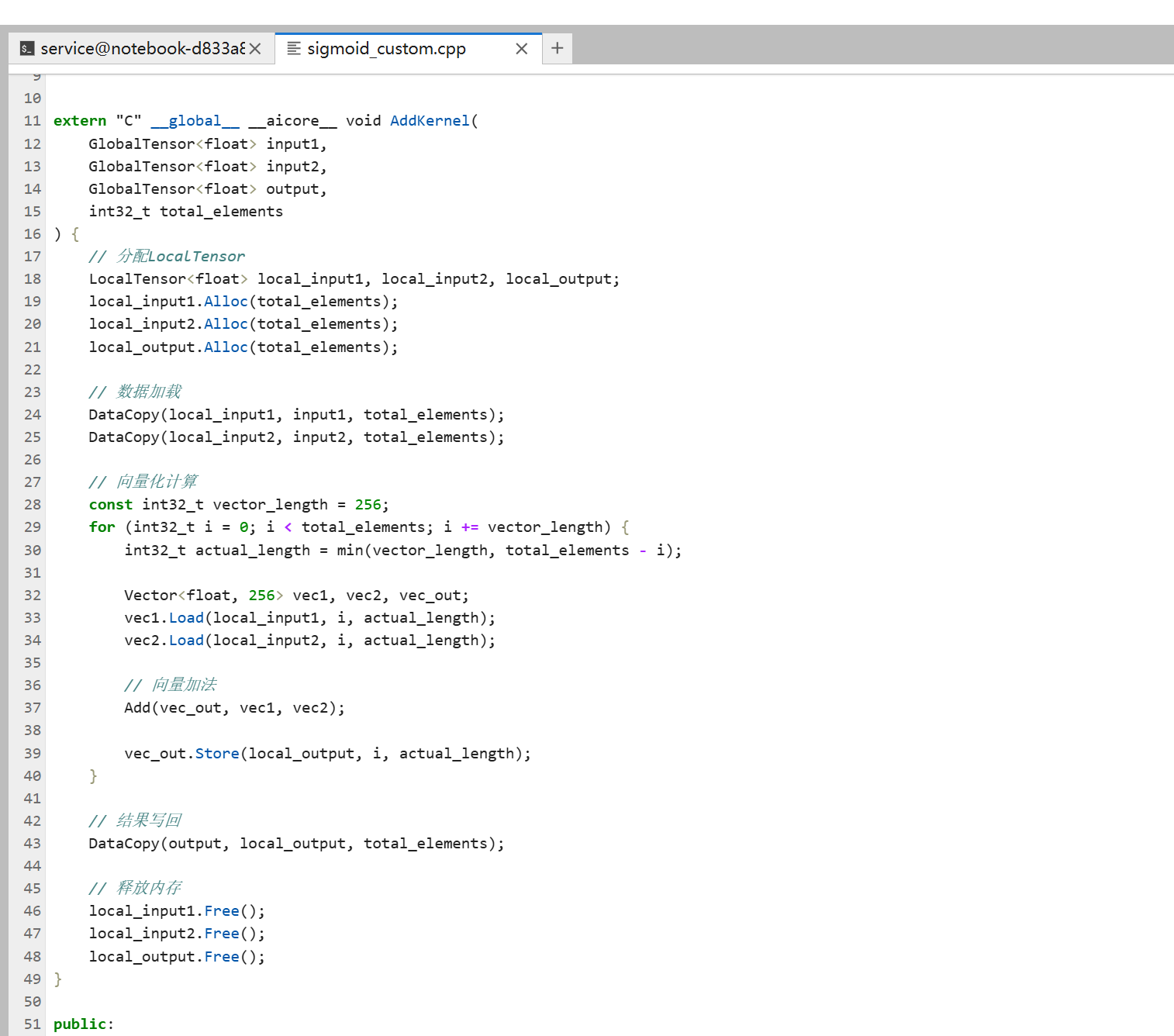
// 概念性示例
extern "C" __global__ __aicore__ void AddKernel(
    GlobalTensor<float> input1,
    GlobalTensor<float> input2,
    GlobalTensor<float> output,
    int32_t total_elements
) {
    // 分配LocalTensor
    LocalTensor<float> local_input1, local_input2, local_output;
    local_input1.Alloc(total_elements);
    local_input2.Alloc(total_elements);
    local_output.Alloc(total_elements);
    
    // 数据加载
    DataCopy(local_input1, input1, total_elements);
    DataCopy(local_input2, input2, total_elements);
    
    // 向量化计算
    const int32_t vector_length = 256;
    for (int32_t i = 0; i < total_elements; i += vector_length) {
        int32_t actual_length = min(vector_length, total_elements - i);
        
        Vector<float, 256> vec1, vec2, vec_out;
        vec1.Load(local_input1, i, actual_length);
        vec2.Load(local_input2, i, actual_length);
        
        // 向量加法
        Add(vec_out, vec1, vec2);
        
        vec_out.Store(local_output, i, actual_length);
    }
    
    // 结果写回
    DataCopy(output, local_output, total_elements);
    
    // 释放内存
    local_input1.Free();
    local_input2.Free();
    local_output.Free();
}

实现要点：元素级算子实现起来比较简单，主要是向量化循环，用Add API做向量加法。注意处理边界情况，如果元素数不是向量长度的倍数，要处理剩余的元素。

Sub、Mul、Div算子

Sub、Mul、Div算子和Add类似，只是用的API不同：

Sub算子：用Sub API，两个向量相减。

Mul算子：用Mul API，两个向量相乘。

Div算子：用Div API，两个向量相除。

实现思路都一样，就是加载数据、向量化计算、写回结果。

ReLU激活函数

ReLU是max(0, x)，就是如果x小于0就输出0，否则输出x。

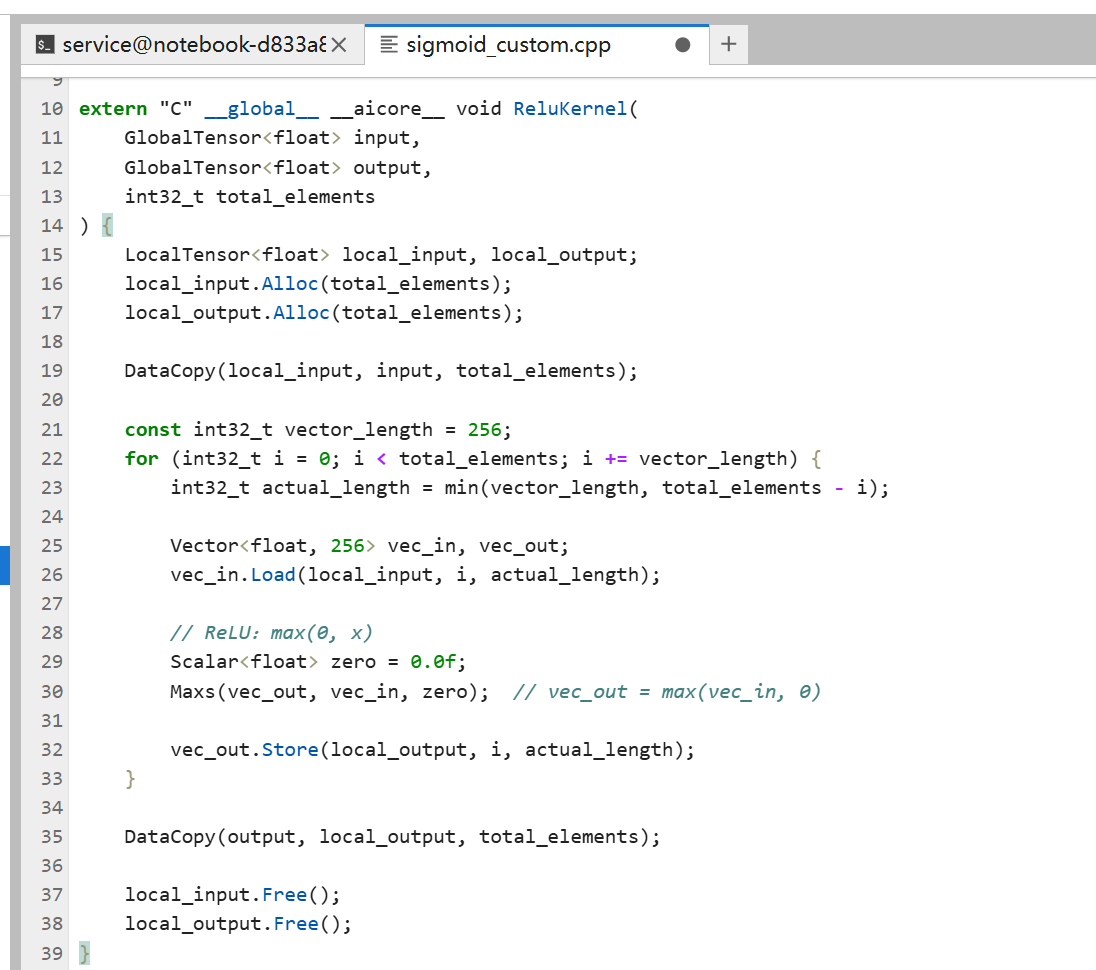
// 概念性示例
extern "C" __global__ __aicore__ void ReluKernel(
    GlobalTensor<float> input,
    GlobalTensor<float> output,
    int32_t total_elements
) {
    LocalTensor<float> local_input, local_output;
    local_input.Alloc(total_elements);
    local_output.Alloc(total_elements);
    
    DataCopy(local_input, input, total_elements);
    
    const int32_t vector_length = 256;
    for (int32_t i = 0; i < total_elements; i += vector_length) {
        int32_t actual_length = min(vector_length, total_elements - i);
        
        Vector<float, 256> vec_in, vec_out;
        vec_in.Load(local_input, i, actual_length);
        
        // ReLU：max(0, x)
        Scalar<float> zero = 0.0f;
        Maxs(vec_out, vec_in, zero);  // vec_out = max(vec_in, 0)
        
        vec_out.Store(local_output, i, actual_length);
    }
    
    DataCopy(output, local_output, total_elements);
    
    local_input.Free();
    local_output.Free();
}

ReLU实现用Maxs API，向量和标量0比较，取最大值。

Sigmoid和Tanh

Sigmoid和Tanh是更复杂的激活函数，需要用到数学函数API。

Sigmoid：sigmoid(x) = 1 / (1 + exp(-x))

// 概念性示例
// Sigmoid实现
Vector<float, 256> vec_in, vec_neg, vec_exp, vec_one, vec_out;

// vec_neg = -vec_in
Muls(vec_neg, vec_in, -1.0f);

// vec_exp = exp(-vec_in)
Exp(vec_exp, vec_neg);

// vec_one = 1 + exp(-vec_in)
Scalar<float> one = 1.0f;
Adds(vec_one, vec_exp, one);

// vec_out = 1 / (1 + exp(-vec_in))
Reciprocal(vec_out, vec_one);

Tanh：tanh(x) = (exp(2x) - 1) / (exp(2x) + 1)

实现思路类似，用Exp、Add、Sub、Div这些API组合起来。

Abs、Sqrt、Exp、Log

这些是数学函数算子，直接用对应的API就行：

Abs：用Abs API，取绝对值。

Sqrt：用Sqrt API，开平方。

Exp：用Exp API，自然指数。

Ln：用Ln API，自然对数。

实现都很简单，向量化循环，调用对应的API。

4.1.2 规约算子（Reduction）

什么是规约算子

规约算子就是把一个张量的所有元素归约成一个值或几个值。比如Sum把所有元素加起来，Max找最大值。

规约算子的特点是需要遍历所有元素，然后归约。实现起来比元素级算子复杂一些。

Sum算子实现

Sum算子就是把所有元素加起来。

// 概念性示例
extern "C" __global__ __aicore__ void SumKernel(
    GlobalTensor<float> input,
    GlobalTensor<float> output,
    int32_t total_elements
) {
    LocalTensor<float> local_input;
    local_input.Alloc(total_elements);
    
    DataCopy(local_input, input, total_elements);
    
    // 先对每个块求和
    const int32_t vector_length = 256;
    LocalTensor<float> block_sums;
    int32_t num_blocks = (total_elements + vector_length - 1) / vector_length;
    block_sums.Alloc(num_blocks);
    
    for (int32_t i = 0; i < total_elements; i += vector_length) {
        int32_t actual_length = min(vector_length, total_elements - i);
        
        Vector<float, 256> vec;
        vec.Load(local_input, i, actual_length);
        
        // 对当前块求和
        Scalar<float> block_sum;
        ReduceSum(block_sum, vec);
        
        // 保存块的和
        block_sum.Store(block_sums, i / vector_length);
    }
    
    // 对所有块的和再求和
    Scalar<float> total_sum = 0.0f;
    for (int32_t i = 0; i < num_blocks; i++) {
        Scalar<float> block_sum;
        block_sum.Load(block_sums, i);
        total_sum = total_sum + block_sum;
    }
    
    // 写回结果
    total_sum.Store(output, 0);
    
    local_input.Free();
    block_sums.Free();
}

实现要点：规约算子通常分两步，先对每个块归约，再对所有块的结果归约。这样可以充分利用向量化。

Mean算子

Mean就是Sum除以元素个数：

// 概念性示例
// 先求和
SumKernel(input, sum_output, total_elements);

// 再除以元素个数
Scalar<float> sum, mean;
sum.Load(sum_output, 0);
mean = sum / total_elements;
mean.Store(output, 0);

Max和Min算子

Max和Min找最大值和最小值，实现思路和Sum类似，用ReduceMax和ReduceMin API。

// 概念性示例
// Max实现
Vector<float, 256> vec;
Scalar<float> max_val;
ReduceMax(max_val, vec);

ArgMax和ArgMin

ArgMax和ArgMin不仅要找最大值最小值，还要找对应的索引位置。

// 概念性示例
// ArgMax实现
Vector<float, 256> vec;
Scalar<float> max_val;
Scalar<int32_t> max_idx;
ReduceMaxWithIndex(max_val, max_idx, vec);  // 同时返回值和索引

4.1.3 索引算子

Gather算子

Gather算子根据索引从输入张量中收集元素。

// 概念性示例
extern "C" __global__ __aicore__ void GatherKernel(
    GlobalTensor<float> input,
    GlobalTensor<int32_t> indices,
    GlobalTensor<float> output,
    int32_t num_indices,
    int32_t input_size
) {
    LocalTensor<float> local_input, local_output;
    LocalTensor<int32_t> local_indices;
    
    local_input.Alloc(input_size);
    local_indices.Alloc(num_indices);
    local_output.Alloc(num_indices);
    
    DataCopy(local_input, input, input_size);
    DataCopy(local_indices, indices, num_indices);
    
    // 根据索引收集元素
    for (int32_t i = 0; i < num_indices; i++) {
        Scalar<int32_t> idx;
        idx.Load(local_indices, i);
        
        Scalar<float> value;
        value.Load(local_input, idx.GetValue());
        
        value.Store(local_output, i);
    }
    
    DataCopy(output, local_output, num_indices);
    
    local_input.Free();
    local_indices.Free();
    local_output.Free();
}

实现要点：Gather需要根据索引访问输入，索引访问可能不是连续的，所以性能可能不如元素级算子。

Scatter算子

Scatter是Gather的反向操作，根据索引把值散布到输出张量中。

// 概念性示例
// Scatter实现
for (int32_t i = 0; i < num_indices; i++) {
    Scalar<int32_t> idx;
    Scalar<float> value;
    
    idx.Load(local_indices, i);
    value.Load(local_input, i);
    
    // 散布到输出
    value.Store(local_output, idx.GetValue());
}

注意Scatter可能有索引冲突，多个输入值要散布到同一个位置，需要定义合并规则（比如相加、取最大值等）。

IndexSelect算子

IndexSelect是Gather的特殊情况，沿着某个维度选择元素。

实现思路和Gather类似，但需要处理多维张量的索引计算。

---

4.2 矩阵运算算子

4.2.1 矩阵乘法（MatMul）

MatMul的基本原理

矩阵乘法是深度学习里最常用的运算。两个矩阵A和B相乘，A是[m, k]，B是[k, n]，结果C是[m, n]。

计算规则是：C[i, j] = sum(A[i, :] * B[:, j])

MatMul的实现思路

矩阵乘法实现起来比较复杂，主要考虑：

分块（Tiling）：大矩阵要分块处理，每块的大小要适合Local Memory。

数据重用：A的行和B的列可以重用，要充分利用这个特性。

Cube Unit利用：昇腾处理器有专门的矩阵乘法单元（Cube Unit），要充分利用。

// 概念性示例（简化版）
extern "C" __global__ __aicore__ void MatMulKernel(
    GlobalTensor<float> A,
    GlobalTensor<float> B,
    GlobalTensor<float> C,
    int32_t M, int32_t K, int32_t N
) {
    // 分块大小
    const int32_t tile_m = 64;
    const int32_t tile_k = 64;
    const int32_t tile_n = 64;
    
    // 分配LocalTensor
    LocalTensor<float> local_A, local_B, local_C;
    local_A.Alloc(tile_m * tile_k);
    local_B.Alloc(tile_k * tile_n);
    local_C.Alloc(tile_m * tile_n);
    
    // 初始化C为0
    Memset(local_C, 0, tile_m * tile_n);
    
    // 分块计算
    for (int32_t m = 0; m < M; m += tile_m) {
        for (int32_t n = 0; n < N; n += tile_n) {
            // 初始化当前块的C
            Memset(local_C, 0, tile_m * tile_n);
            
            // K维度累加
            for (int32_t k = 0; k < K; k += tile_k) {
                // 加载A的块
                LoadTile(local_A, A, m, k, tile_m, tile_k, M, K);
                // 加载B的块
                LoadTile(local_B, B, k, n, tile_k, tile_n, K, N);
                
                // 矩阵乘法：C += A * B
                MatMul(local_C, local_A, local_B, local_C);
            }
            
            // 写回C的块
            StoreTile(C, local_C, m, n, tile_m, tile_n, M, N);
        }
    }
    
    local_A.Free();
    local_B.Free();
    local_C.Free();
}

实现要点：矩阵乘法要分块，充分利用Cube Unit。分块大小要合适，太小了利用率低，太大了Local Memory装不下。

MatMul的优化技巧

数据布局优化：矩阵数据怎么存储很重要，按行存储还是按列存储，影响访问效率。

K维度分块：K维度要分块累加，这样可以重用A和B的数据。

流水线化：加载下一块数据、计算当前块、写回上一块结果，可以流水线化。

4.2.2 矩阵转置（Transpose）

Transpose的基本原理

矩阵转置就是把矩阵的行列互换，A[i, j]变成A[j, i]。

Transpose的实现

// 概念性示例
extern "C" __global__ __aicore__ void TransposeKernel(
    GlobalTensor<float> input,
    GlobalTensor<float> output,
    int32_t height, int32_t width
) {
    LocalTensor<float> local_input, local_output;
    local_input.Alloc(height * width);
    local_output.Alloc(height * width);
    
    DataCopy(local_input, input, height * width);
    
    // 转置
    for (int32_t i = 0; i < height; i++) {
        for (int32_t j = 0; j < width; j++) {
            Scalar<float> value;
            value.Load(local_input, i * width + j);
            value.Store(local_output, j * height + i);
        }
    }
    
    DataCopy(output, local_output, height * width);
    
    local_input.Free();
    local_output.Free();
}

实现要点：转置的访问模式不是连续的，可能影响性能。可以用向量化优化，或者用专门的转置指令。

4.2.3 批处理矩阵乘法（BatchMatMul）

BatchMatMul的基本原理

BatchMatMul就是多个矩阵乘法一起做。输入是[batch, m, k]和[batch, k, n]，输出是[batch, m, n]。

BatchMatMul的实现

// 概念性示例
extern "C" __global__ __aicore__ void BatchMatMulKernel(
    GlobalTensor<float> A,
    GlobalTensor<float> B,
    GlobalTensor<float> C,
    int32_t batch, int32_t M, int32_t K, int32_t N
) {
    for (int32_t b = 0; b < batch; b++) {
        // 每个batch的矩阵乘法
        GlobalTensor<float> A_batch = A[b];
        GlobalTensor<float> B_batch = B[b];
        GlobalTensor<float> C_batch = C[b];
        
        MatMulKernel(A_batch, B_batch, C_batch, M, K, N);
    }
}

实现要点：BatchMatMul可以并行处理不同的batch，充分利用多核。

4.2.4 矩阵分解相关算子

矩阵分解算子比如SVD、QR分解这些，实现起来比较复杂，通常需要调用专门的数学库或者用迭代算法实现。这里就不详细展开了，有兴趣可以查专门的资料。

---

4.3 卷积相关算子

4.3.1 卷积（Convolution）

卷积的基本原理

卷积是深度学习的核心运算。输入是[N, C, H, W]的特征图，卷积核是[K, C, Kh, Kw]，输出是[N, K, H’, W’]。

计算规则是：对输出的每个位置，用卷积核在输入上滑动窗口，计算点积。

卷积的实现思路

卷积实现起来很复杂，主要有几种方法：

直接卷积：按照定义直接计算，简单但慢。

im2col转换：把卷积转换成矩阵乘法，用MatMul实现。

Winograd算法：用Winograd算法加速，减少计算量。

分组卷积优化：如果卷积是分组的，可以优化。

// 概念性示例（im2col方法）
extern "C" __global__ __aicore__ void Conv2DKernel(
    GlobalTensor<float> input,      // [N, C, H, W]
    GlobalTensor<float> weight,     // [K, C, Kh, Kw]
    GlobalTensor<float> output,     // [N, K, H', W']
    int32_t N, int32_t C, int32_t H, int32_t W,
    int32_t K, int32_t Kh, int32_t Kw,
    int32_t stride_h, int32_t stride_w,
    int32_t pad_h, int32_t pad_w
) {
    // 1. im2col：把输入转换成矩阵
    // 2. 矩阵乘法：weight * im2col(input)
    // 3. col2im：把结果转换回特征图格式
}

实现要点：卷积通常用im2col转换成矩阵乘法，然后用MatMul实现。im2col有内存开销，但实现简单，性能也不错。

4.3.2 池化（Pooling）

池化的基本原理

池化是对特征图做下采样，常见的有MaxPooling和AvgPooling。

MaxPooling：在窗口内取最大值。

AvgPooling：在窗口内取平均值。

MaxPooling实现

// 概念性示例
extern "C" __global__ __aicore__ void MaxPool2DKernel(
    GlobalTensor<float> input,
    GlobalTensor<float> output,
    int32_t N, int32_t C, int32_t H, int32_t W,
    int32_t kernel_h, int32_t kernel_w,
    int32_t stride_h, int32_t stride_w
) {
    // 对每个输出位置
    for (int32_t n = 0; n < N; n++) {
        for (int32_t c = 0; c < C; c++) {
            for (int32_t oh = 0; oh < output_h; oh++) {
                for (int32_t ow = 0; ow < output_w; ow++) {
                    // 在窗口内找最大值
                    float max_val = -INF;
                    for (int32_t kh = 0; kh < kernel_h; kh++) {
                        for (int32_t kw = 0; kw < kernel_w; kw++) {
                            int32_t ih = oh * stride_h + kh;
                            int32_t iw = ow * stride_w + kw;
                            float val = input[n][c][ih][iw];
                            max_val = max(max_val, val);
                        }
                    }
                    output[n][c][oh][ow] = max_val;
                }
            }
        }
    }
}

实现要点：池化可以向量化，对多个通道并行处理。也可以用专门的池化指令。

4.3.3 反卷积（Deconvolution）

反卷积也叫转置卷积，是卷积的逆操作。实现思路和卷积类似，但更复杂一些。通常也用im2col或者专门的算法实现。

4.3.4 分组卷积（Group Convolution）

分组卷积是把输入通道分成几组，每组独立做卷积，最后把结果拼接起来。这样可以减少计算量，适合深度可分离卷积这种场景。

实现要点：分组卷积可以并行处理不同的组，充分利用多核。

---

4.4 归一化算子

4.4.1 BatchNorm

BatchNorm的基本原理

BatchNorm是对每个通道在batch维度上做归一化。计算步骤：

1. 计算均值和方差：mean = mean(x), var = var(x)
2. 归一化：y = (x - mean) / sqrt(var + eps)
3. 缩放和平移：y = gamma * y + beta

BatchNorm的实现

// 概念性示例
extern "C" __global__ __aicore__ void BatchNormKernel(
    GlobalTensor<float> input,
    GlobalTensor<float> output,
    GlobalTensor<float> gamma,
    GlobalTensor<float> beta,
    GlobalTensor<float> running_mean,
    GlobalTensor<float> running_var,
    int32_t N, int32_t C, int32_t H, int32_t W,
    float eps
) {
    // 1. 计算均值和方差（规约操作）
    // 2. 归一化
    // 3. 缩放和平移
}

实现要点：BatchNorm需要先做规约（计算均值和方差），再做元素级运算（归一化、缩放、平移）。

4.4.2 LayerNorm

LayerNorm的基本原理

LayerNorm是对每个样本在特征维度上做归一化。和BatchNorm的区别是归一化的维度不同。

实现思路和BatchNorm类似，也是先规约再归一化，但规约的维度不同。

4.4.3 InstanceNorm和GroupNorm

InstanceNorm和GroupNorm是BatchNorm的变种，归一化的维度不同：

InstanceNorm：对每个样本的每个通道独立归一化。

GroupNorm：把通道分组，对每组独立归一化。

实现思路都类似，主要是规约的维度不同。

---

学习检查点

学完这一篇，你应该能做到这些：

理解各种常用算子的实现方法，包括元素级算子、规约算子、索引算子。掌握矩阵运算算子的实现，特别是矩阵乘法的分块策略。了解卷积相关算子的实现思路，知道im2col等方法。理解归一化算子的实现，知道如何组合规约和元素级运算。

实践练习

实现ReLU算子：实现一个ReLU激活函数算子，用向量化API，完成从编写到测试的全流程。

实现Sum算子：实现一个Sum规约算子，先对块归约，再对块结果归约，理解规约的实现方法。

优化矩阵乘法：实现一个简单的矩阵乘法算子，尝试不同的分块大小，看看性能差异。理解Tiling策略的重要性。

实现简单卷积：用im2col方法实现一个简单的2D卷积，理解卷积如何转换成矩阵乘法。

---

下一步：掌握了常用算子的实现后，就可以学习高级优化技术了。下一章会讲性能优化、精度优化、算子融合这些高级话题，到时候你就能写出高性能的算子了。

2025年昇腾CANN训练营第二季，基于CANN开源开放全场景，推出0基础入门系列、码力全开特辑、开发者案例等专题课程，助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证，即可领取精美证书，完成社区任务更有机会赢取华为手机，平板、开发板等大奖。

报名链接:https://www.hiascend.com/developer/activities/cann20252

社区地址：https://www.hiascend.com/developer