快速幂算法 超详细教程

https://blog.csdn.net/m0_52072919/article/details/116400820

快速幂

• 求幂运算
• 快速幂引入
• 快速幂 二进制
• 快速幂 指数折半
• 快速幂的应用

求幂运算

求幂运算大家都不陌生，幂是指数运算的结果，当m是正整数时nᵐ的意义为m个n相乘，n的m次幂也就是n的m次方。用代码实现求幂运算可以这样写：

long long int mypower(int base, int power)
{
    long long int result = 1;
    
    for (int i = 1; i <= power; i++)
        result *= base;
        
    return result;
}

运行测试结果也是正确的

但我们可以分析一下他的时间复杂度，时间复杂度为O(power)，power指数越大程序循环次数更多，2的3次方需要循环3次，2的100次方要循环一百次，如果是2的1000000次方那就得循环一百万次，显然在时间上要花费更多。有没有什么方法可以有效减少循环次数从而避免大量时间的开支呢？为了解决这个问题我们引入了新算法，快速幂。

快速幂引入

为了方便大家理解，我会用两种角度去讲解快速幂算法，二进制与指数折半，其实这两个的本质是一样的，只是分析的角度有些许不同，大家可以按照适合自己的角度去理解快速幂算法，当然两种角度都了解了，那更是最好了。

快速幂 二进制

核心思想：利用二进制来加速运算
例如：nᵐ中m = 11(10)。十进制的11转换为为二进制是1011(2)。

到这里快速幂的思想出来了，上面的描述我们可以用代码实现

long long int quik_power(int base, int power)
{
    long long int result = 1;   //用于存储项累乘与返回最终结果，由于要存储累乘所以要初始化为1
    while (power > 0)           //指数大于0说明指数的二进制位并没有被左移舍弃完毕
    {
        if (power & 1)          //指数的当前计算二进制位也就是最末尾的位是非零位也就是1的时候
                                //例如1001的当前计算位就是1， 100*1* 星号中的1就是当前计算使用的位
            result *= base;     //累乘当前项并存储
        base *= base;           //计算下一个项，例如当前是n^2的话计算下一项n^2的值
                                //n^4 = n^2 * n^2;
        power >>= 1;            //指数位右移，为下一次运算做准备
                                //一次的右移将舍弃一个位例如1011(2)一次左移后变成101(2)
    }
    return result;              //返回最终结果
}

为了便于理解我们分析一个实例
 

快速幂 指数折半

核心思想：每一次运算都把指数折半，底数变其平方
 

long long int quik_power(int base, int power)
{
	long long int result = 1;
	while (power > 0)           //指数大于0进行指数折半，底数变其平方的操作
	{
		if (power % 2 == 1)     //指数为奇数
		{
			power -= 1;         //指数减一
			power /= 2;         //指数折半
			result *= base;     //分离出当前项并累乘后保存
			base *= base;       //底数变其平方
		}
		else                    //指数为偶数
		{
			power /= 2;         //指数折半
			base *= base;       //底数变其平方
		}
	}
	return result;              //返回最终结果
}

我们不难发现代码中有重复的语句所以我们可以稍加优化整理。

 	power /= 2;         //指数折半
    base *= base;       //底数变其平方

不管指数是否为奇数偶数，指数折半和底数变其平方是都需要进行的必要操作我们可以直接写在判断语句外面

long long int quik_power(int base, int power)
{
	long long int result = 1;
	while (power > 0)           //指数大于0进行指数折半，底数变其平方的操作
	{
		if (power % 2 == 1)     //指数为奇数
		{
			power -= 1;         //指数减一
			result *= base;     //分离出当前项并累乘后保存
		}
		power /= 2;         //指数折半
		base *= base;       //底数变其平方
	}
	return result;              //返回最终结果
}

还有一些多余代码我们也能删除。

	power -= 1;         //指数减一

如果指数是奇数的话有个减一操作，但在代码中我们可以省略这个，因为代码中指数是整数int类型，当power是奇数时小数点会被舍弃，这相当于power减一后再除二的操作。例如：power= 3的时候power / 2 = 相当于power-1后power=2后power / 2 = 1。所以代码可以写成这样。

long long int quik_power(int base, int power)
{
	long long int result = 1;
	while (power > 0)           //指数大于0进行指数折半，底数变其平方的操作
	{
		if (power % 2 == 1)     //指数为奇数
			result *= base;     //分离出当前项并累乘后保存
		power /= 2;        	    //指数折半
		base *= base;           //底数变其平方
	}
	return result;              //返回最终结果
}

判断一个数的奇数偶数时，除了判断能否被二整除以外我们还有一个方法就是看那个数的二进制。

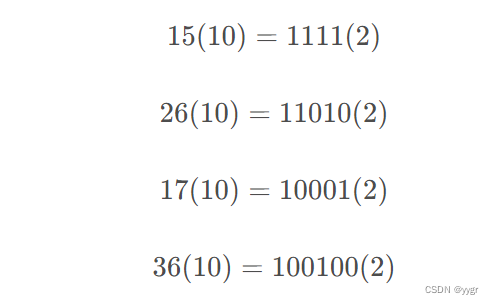
我们可以发现一个规律，奇数的二进制位末尾是1，偶数的二进制位是0.位运算要比取余运算要快所以我们可以把代码写成这样。

long long int quik_power(int base, int power)
{
	long long int result = 1;
	while (power > 0)           //指数大于0进行指数折半，底数变其平方的操作
	{
		if (power & 1)			//指数为奇数，power & 1这相当于power % 2 == 1
			result *= base;     //分离出当前项并累乘后保存
		power /= 2;			    //指数折半
		base *= base;           //底数变其平方
	}
	return result;              //返回最终结果
}

我们还可以替换一些代码使程序运算效率更高。

	power /= 2;			    //指数折半

这里的指数折半操作我们也可以使用位运算的左移运算来完成。位运算比除于运算要快。所以我们可以这样写代码。

long long int quik_power(int base, int power)
{
	long long int result = 1;
	while (power > 0)           //指数大于0进行指数折半，底数变其平方的操作
	{
		if (power & 1)			//指数为奇数，power & 1这相当于power % 2 == 1
			result *= base;     //分离出当前项并累乘后保存
		power >>= 1;			//指数折半,power >>= 1这相当于power /= 2;
		base *= base;           //底数变其平方
	}
	return result;              //返回最终结果
}

这就是我们最终的快速幂代码了。大家可能发现了，在快速幂算法中二进制角度还是指数折半角度最终写出的代码其实是一样的只是理解角度略有不同罢了。

快速幂的应用

快速幂一般不会独立使用，常常配合取余运算法则来使用。
看下面这两个题：
HDOJ 2035 人见人爱A^B
HDOJ 1061 Rightmost Digit
做这两个题前首先我们需要了解一下关于取余的公式
(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p ) % p
(a * b) % p = (a % p * b % p) % p
我们可以把公式三加入我们的快速幂代码中

long long int quik_power(int base, int power, int p)
{
	long long int result = 1;   
	while (power > 0)           
	{
		if (power & 1)         							
			result = result * base % p;   
			//根据公式每个项都取余数后在再做累乘
		base = base * base % p ;   
			//根据公式每个项都取余数后在再做平方操作      						
		power >>= 1;         						
	}
			//根据公式在最后的的结果上再来一次取余数
	return result % p;       
}

那两个题的题解我就不在这写了。特别出两个博客了。感兴趣的朋友可以去看看。
HDOJ 1061 Rightmost Digit 题解
HDOJ 2035 人见人爱A^B 题解