2.3.1 分治法
分治法由两部分构成:分治+递归
最开始接触递归,是在用递归的方法求解斐波那契数列那会。
斐波那契数很简单,定义如下:
用递归的方法求斐波那契数列和
int Fibonacci(int n)
{
if(n<=1)
return n;
else
return Fibonacci(n-1)+Fibonacci(n-2);
}分治法的思想和递归有些相像,它把一个大规模的问题分解成更小的但是算法逻辑相似的问题,不断往下递归,最后由得到的最小问题的解逐层往上构成所求问题的解。
体现分治法的一个典型例子就是归并排序
MERGE-SORT(A,p,r)
if p<r
q=(r-p)/2
MERGE-SORT(A,p,q)
MERGE-SORT(A,q+1,r)
MERGE(A,p,q,r)
MERGE(A,p,q,r)
n1=q-p+1
n2=r-q+1
for i=1 to n1
L[i]=A[p+i-1]
for j=1 to n2
R[j]=A[q+j]
L[n1+1]=65535
R[n2+1]=65535
i=1
j=1
for k=p to r
if L[i]<=R[j]
A[k]=L[i]
i=i+1
else
A[k]=R[j]
j=j+1
贴一张归并排序的简单图解
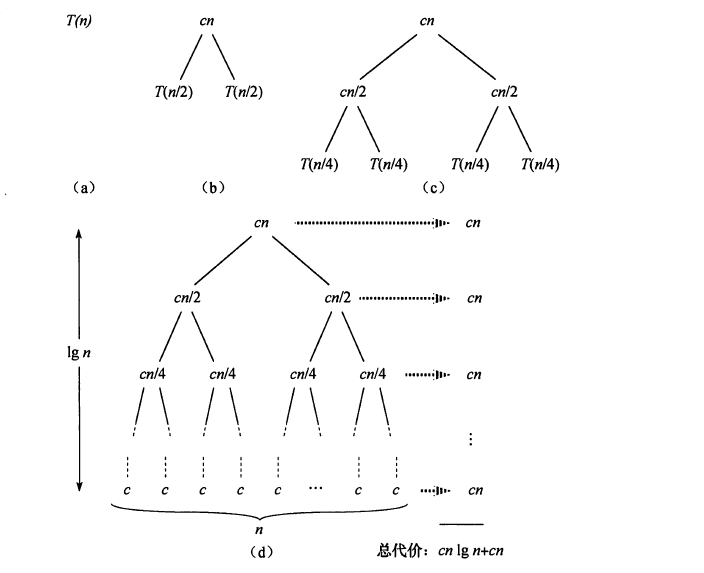
2.2.3 分析分治算法
注:cn为树根(在递归的顶层引起的代价)
根的两个子树代表较小的规模(T(n/2))
T(n)=2T(n/2)+cn=.....=c*n*( lg n+1 )
=θ(n*lg n)
2.3-2:重写MERGE伪代码(不使用无穷大哨兵)
MERGE(A,p,q,r)
n1=q-p+1
n2=r-q+1
for i=1 to n1
L[i]=A[p+i-1]
for j=1 to n2
R[j]=A[q+j]
L[n1+1]=65535
R[n2+1]=65535
i=1
j=1
for k=p to r
if i>n1 or j>n2
break
if L[i]<=R[j]
A[k]=L[i]
i=i+1
else
A[k]=R[j]
j=j+1
if i>n1
for j to n2
A[P+n1+j-1]=R[j]
else
for i to n1
A[P+n2+i-1]=L[i]2.3-3 n=2^1 成立
假设当n=2^p,解T(n)=n*lg n成立
当n'=2^(p+1)时,T(n')=.....=T(n+1)
由数学归纳法,证明完毕。
2.3-4
推导可得: T(n)=θ(n^2)
2.3-5
binarySearch(A,p,q)
if p>q
return NIL
if v>A[(p+q)/2]
binarySearch(A,(p+q)/2,q)
else if v<A[(p+q)/2]
binarySearch(A,p,(p+q)/2)
else
return (p+q)/2
时间成本分析:每迭代一次,规模减半。
T(n)=T(n/2)+θ(1)
求解得T(n)=lg n









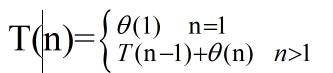














 276
276

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








