红黑树rbtree

• 红黑树规则

• 一颗典型的红黑树如图

• 红黑树性质

1. 节点不是黑色，就是红色（非黑即红）
2. 根节点为黑色
3. 叶节点为黑色（叶节点是指末梢的空节点 Nil或Null,也可以用一个特殊的节点专门表示叶节点）
4. 一个节点为红色，则其两个子节点必须是黑色的（根到叶子的所有路径，不可能存在两个连续的红色节点）
5. 每个节点到叶子节点的所有路径，都包含相同数目的黑色节点（相同的黑色高度）

注意：性质4和5，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树

• 红黑树定义

#define RED				1
#define BLACK 			2

typedef int KEY_TYPE;

typedef struct _rbtree_node {
	unsigned char color;
	struct _rbtree_node *right;
	struct _rbtree_node *left;
	struct _rbtree_node *parent;
	KEY_TYPE key;
	void *value;
} rbtree_node;

typedef struct _rbtree {
	rbtree_node *root;
	rbtree_node *nil;//专门用来表示叶子节点
} rbtree;

• 红黑树的基本操作（旋转）

1：左旋

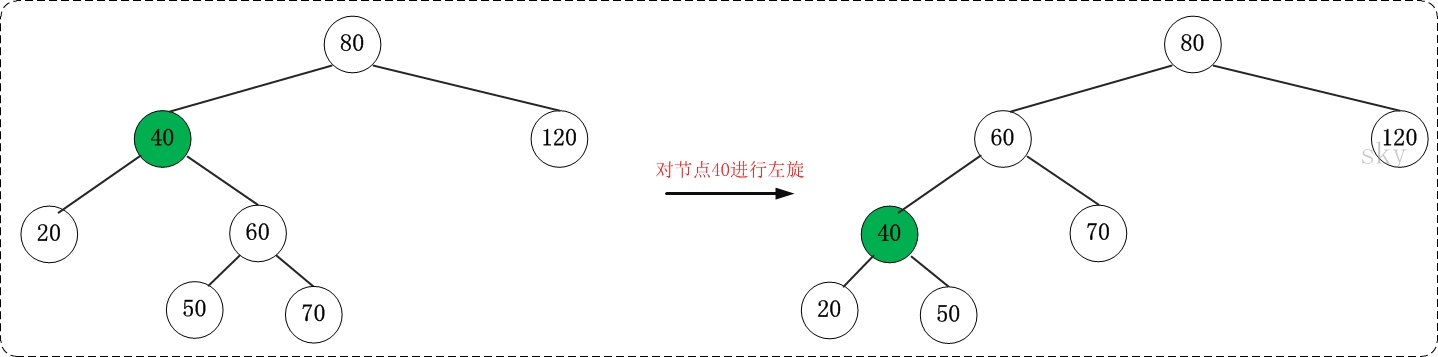
2：右旋

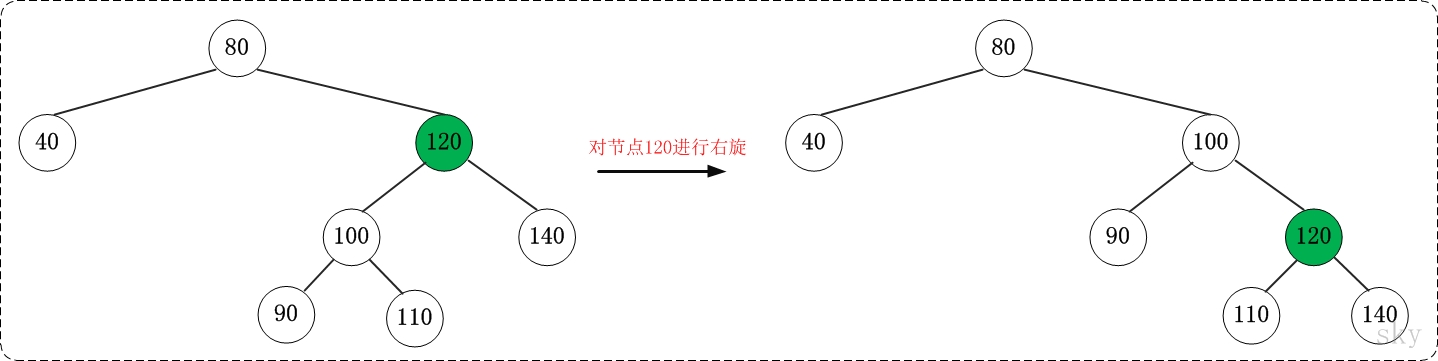
3：旋转总结：

左旋图：对旋转后的40节点，以40的父节点为中心，进行右旋，将回到左旋之前

右旋图：对旋转后的120节点，以120的父节点100为中心，进行左旋，将回到右旋之前

 如上图左旋右旋相互转换

4：代码：

void rbtree_left_rotate(rbtree *T, rbtree_node *x) {

	rbtree_node *y = x->right;  // x  --> y  ,  y --> x,   right --> left,  left --> right

	x->right = y->left; //1 1
	if (y->left != T->nil) { //1 2
		y->left->parent = x;
	}

	y->parent = x->parent; //1 3
	if (x->parent == T->nil) { //1 4
		T->root = y;
	} else if (x == x->parent->left) {
		x->parent->left = y;
	} else {
		x->parent->right = y;
	}

	y->left = x; //1 5
	x->parent = y; //1 6
}


void rbtree_right_rotate(rbtree *T, rbtree_node *y) {

	rbtree_node *x = y->left;

	y->left = x->right;
	if (x->right != T->nil) {
		x->right->parent = y;
	}

	x->parent = y->parent;
	if (y->parent == T->nil) {
		T->root = x;
	} else if (y == y->parent->right) {
		y->parent->right = x;
	} else {
		y->parent->left = x;
	}

	x->right = y;
	y->parent = x;
}

如图左旋和右旋代码，右旋就是在左旋代码的基础上，将  X>>Y,   Y>>X,   right>>left,   left>>right。