

 ,然后我们确立一系列独立随机变量:
,然后我们确立一系列独立随机变量:
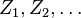
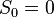
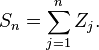
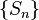 可以称为在
可以称为在
 上的简单随机漫步。该集合是所以1和-1的相加,并计算出漫步距离。
上的简单随机漫步。该集合是所以1和-1的相加,并计算出漫步距离。
 的期望值
的期望值
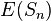 为0,也即是说,如果掷硬币的次数增加,每次掷硬币所得到的值的平均数会趋向于0,有限次数相加的期望值为:
为0,也即是说,如果掷硬币的次数增加,每次掷硬币所得到的值的平均数会趋向于0,有限次数相加的期望值为:
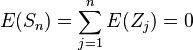
 ,变换成另一个类似的计算公式则为:
,变换成另一个类似的计算公式则为:
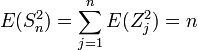
 ,大约为
,大约为
 。事实上,我们能够知道:
。事实上,我们能够知道:

 上的简单随机漫步能够在无限次数中经过所有的点,这样的过程有不同的名字
上的简单随机漫步能够在无限次数中经过所有的点,这样的过程有不同的名字
How many times will a random walk cross a boundary line if permitted to continue walking forever? A simple random walk on  will cross every point an infinite number of times. This result has many names: the level-crossing phenomenon, recurrence or the gambler's ruin. The reason for the last name is as follows: a gambler with a finite amount of money will eventually lose when playing a fair game against a bank with an infinite amount of money. The gambler's money will perform a random walk, and it will reach zero at some point, and the game will be over.
will cross every point an infinite number of times. This result has many names: the level-crossing phenomenon, recurrence or the gambler's ruin. The reason for the last name is as follows: a gambler with a finite amount of money will eventually lose when playing a fair game against a bank with an infinite amount of money. The gambler's money will perform a random walk, and it will reach zero at some point, and the game will be over.
If a and b are positive integers, then the expected number of steps until a one-dimensional simple random walk starting at 0 first hits b or −a is ab. The probability that this walk will hit b before −a is 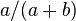 , which can be derived from the fact that simple random walk is a martingale.
, which can be derived from the fact that simple random walk is a martingale.
Some of the results mentioned above can be derived from properties of Pascal's triangle. The number of different walks of n steps where each step is +1 or −1 is clearly 2n. For the simple random walk, each of these walks are equally likely. In order for Sn to be equal to a number k it is necessary and sufficient that the number of +1 in the walk exceeds those of −1 by k. The number of walks which satisfy  is equally the number of ways of choosing (n + k)/2 elements from an n element set,[citation needed] denoted
is equally the number of ways of choosing (n + k)/2 elements from an n element set,[citation needed] denoted 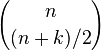 . For this to be non-zero, it is necessary that n + k be an even number. Therefore, the probability that
. For this to be non-zero, it is necessary that n + k be an even number. Therefore, the probability that  is equal to
is equal to  . By representing entries of Pascal's triangle in terms of factorials and using Stirling's formula, one can obtain good estimates for these probabilities for large values of
. By representing entries of Pascal's triangle in terms of factorials and using Stirling's formula, one can obtain good estimates for these probabilities for large values of  .
.
If the space is confined to  + for brevity, the number of ways in which a random walk will land on any given number having five flips can be shown as {0,5,0,4,0,1}.
+ for brevity, the number of ways in which a random walk will land on any given number having five flips can be shown as {0,5,0,4,0,1}.
This relation with Pascal's triangle is demonstrated for small values of n. At zero turns, the only possibility will be to remain at zero. However, at one turn, there is one chance of landing on −1 or one chance of landing on 1. At two turns, a marker at 1 could move to 2 or back to zero. A marker at −1, could move to −2 or back to zero. Therefore, there is one chance of landing on −2, two chances of landing on zero, and one chance of landing on 2.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
![P[S_0=k]](http://upload.wikimedia.org/math/9/0/b/90b7f46f410bd925b2f842562940783b.png) | 1 | ||||||||||
![2P[S_1=k]](http://upload.wikimedia.org/math/2/1/3/213e6059c0811bd0629f64a17c69f440.png) | 1 | 1 | |||||||||
![2^2P[S_2=k]](http://upload.wikimedia.org/math/b/d/2/bd2ff62ebfd09e6aa515c409270fca40.png) | 1 | 2 | 1 | ||||||||
![2^3P[S_3=k]](http://upload.wikimedia.org/math/d/a/4/da423331326e0adc1ebe0f7ed0d78467.png) | 1 | 3 | 3 | 1 | |||||||
![2^4P[S_4=k]](http://upload.wikimedia.org/math/7/a/5/7a59bb11df10fa23c93f7750a7efcaf0.png) | 1 | 4 | 6 | 4 | 1 | ||||||
![2^5P[S_5=k]](http://upload.wikimedia.org/math/3/8/1/381c0144fb19f20a334571825b7c4b91.png) | 1 | 5 | 10 | 10 | 5 | 1 |
The central limit theorem and the law of the iterated logarithm describe important aspects of the behavior of simple random walk on  . In particular, the former entails that as n increases, the probabilities (proportional to the numbers in each row) approach a normal distribution.
. In particular, the former entails that as n increases, the probabilities (proportional to the numbers in each row) approach a normal distribution.
 ,其中某些数
,其中某些数
 ,转换概率(表示从state i到state j的概率)则为
,转换概率(表示从state i到state j的概率)则为
 。
。









 ;这样的例子包括drunkard's walk和
;这样的例子包括drunkard's walk和














 9792
9792

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








