机器学习入门系列之二---线性回归算法学习

   线性回归算法学习还是使用系列一监督算法中涉及的案例（房价分析），那么我们如何使用线性回归算法呢？

  首先我们要开始算法初始化设置工作：

  设置算法训练数据集 (人工标注的正确答案数据设置)

• 算法符号定义(所有的算法学习中统一使用符号)
  • m = 训练集的标注数据总数，训练样本的数量
  • x = 输入变量 （特征变量）这个例子中代表房屋面积 / 准备交给算法进行预测分析
  • y = 输出变量 （目标变量）预测数据，也是算法目标数据
    • (x,y) - 表示训练集中的一个样本
    • (xⁱ, y^j) - 训练集中第i个样本
      
      • i 是训练集的索引，表示第i行

（训练集设置图片，m有47个数据，代表我们的训练集有47个数据）

• 使用算法进行预测的步骤呢?
  • 首先找到训练集合数据
  • 将有m个训练数据组成的训练集合提供给学习算法
  • 学习算法会生成一个输出函数 ，由于历史原因我们用h来表示这个函数，这个函数叫‘假设’
    • 函数h的任务就是接收输入参数 (这里就是需要预测房价的房屋面积)
    • 函数h的输出就是估计出的房价
    • 假设函数将输入x映射到输出y
• 学习算法的第一步就是如何来表述假设，我们对假设使用线性表示
• 我们如何来表示这个函数h呢，定义算法 ?
  • 我们把函数 h表示为下面的公式;
    • h_θ(x) = θ₀ + θ₁x1
    • x-表示输入特征，就是房屋面积
    • 通常回归算法问题都不止一个特征，需要多个输入特征，比如：
    • 我们还知道房屋中卧室的数量，那么我们的训练数据集合就有了第二个特征
    • 用x1表示房子面积 用x2表示房屋卧室的数量
    • 两个特征使用这样函数描述
    • h(x)=h_θ(x) = θ₀ + θ₁x1+θ2x2
    • 
      

• • h_θ(x) = θ₀ + θ₁x是神马意思呢?
  • h_{θ是对于特征X预测的花费， θ是学习算法中的参数，都是实数，利用训练集合选择或学习得到合适的参数值，是学习算法的任务}
  • _{所以给定房子的特征x（一个明确的房屋面积与它有多少卧室），这就是我的假设预测出的开销}
  • _{为了把公式定义的更加简洁，我可以定义X0=1，这样公式就如下图所示：}
    
  • _{i从0-2进行变化，对进行求和，如果你将也作为像X一样的向量，可以写成图片最右侧的形式。}

                   最后一个算法符号

                      n=#features   学习问题中特征的数目，上图中的2就应该替换为n，特指上例时，n=2，函数如下图所示

那么我们怎样选择参数呢？让我们的假设h对所有的房屋做出正确的预测呢？

        一个合理的假设是基于我们的训练数据集合，我们的h会做一些对训练集合中的房子的房价进行预测，我们可以尝试让学习算法的预测在训练数据上尽可能准确，给定一些特征x，以及一些正确的价格y，我们希望取使算法预测和实际价格的平方差尽可能的小。

      如何选择参数，使得参数取时能够使得预测价格和实际价格之差的平方最小，我们有m个训练样本，习惯上我们会在前面乘上1/2而不是直接求平方和，这会简化我们之后的数学运算，

因此我们要做的就是下面这样，最小平方回归，最小二乘问题。这个算法是一类范围更广算法的特例。

• • 最小化θ0/θ1意味着我们得到θ0和θ1的值，当我们在我们的假设函数中使用这些参数时，平均得到x与y的最小偏差
  • 更准确的说，这是一个成本函数
    
    

• 
  而且我们希望最小化这个成本函数
  我们的成本函数（因为summartion术语）固有地在任何时候看训练集中的所有数据
  所以要回顾一下
  假设 - 就像你的预测机器，抛出一个x值，得到一个推定的y值

成本 - 是使用您的训练数据确定θ值的值的方法，使得假设尽可能准确

• • 该成本函数也称为平方误差成本函数
    这个成本函数是大多数回归函数的合理选择
    大概最常用的功能
    如果J（θ0，θ1）有点抽象，进入它的作用，为什么它的工作原理以及我们如何在下一节中使用它

成本功能 - 更深层次观察
让我们考虑一些关于成本函数的直觉，以及为什么要使用它
成本函数确定参数
与参数相关的值决定了您的假设行为，不同的值会产生不同的结果
简化假设

• • Assumes θ₀ = 0

• 这里的成本函数和目标非常类似于当我们有θ0时，但是具有更简单的参数
  简化假设使可视化成本函数J（）更容易一些

• 所以假设通过0,0我们要理解的两个关键功能
• •  h_θ(x)
    
    • 假设是x的函数，x是房屋的尺寸
  • J(θ₁)
    • 是θ1参数的函数
  • So for example
    • θ₁ = 1
    • J(θ₁) = 0
  • Plot
  • • θ₁ vs J(θ₁)
    • Data
    • • 1)
        • θ₁ = 1
        • J(θ₁) = 0
      • 2) 
        • θ₁ = 0.5
        • J(θ₁) = ~0.58
      • 3)
      • • θ₁ = 0
        • J(θ₁) = ~2.3

• • 如果我们计算一个值的范围
  • • J(θ₁) vs θ₁ 我们得到一个多项式（看起来像二次方）

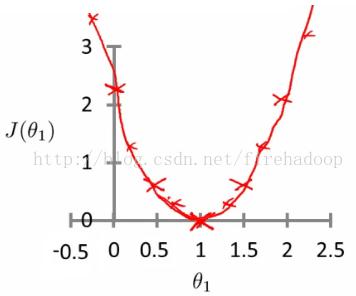
• 学习算法的优化目标是找到最小化J（θ1）的θ1值，
• • So,  θ1= 1是θ1的最佳值

更深入了解成本函数 - 简化成本函数

• 假设你熟悉轮廓图
  使用相同的成本函数，假设和目标如前所述
  如果您不了解cotour图，可以跳过本节的部分
  使用我们原来的复杂的动画与两个pariables，
  所以成本函数是
• • • J(θ₀, θ₁)
• Example,
• • Say 
    • θ₀ = 50
    • θ₁ = 0.06
  • 以前，我们通过绘图绘制了成本函数
    • θ₁ vs J(θ₁)
  • 现在我们有两个参数
    
  • • 情况变得有点复杂
    • 生成轴所在的3D曲面图
    • • X = θ₁
      • Z = θ₀
      • Y = J(θ₀,θ₁)

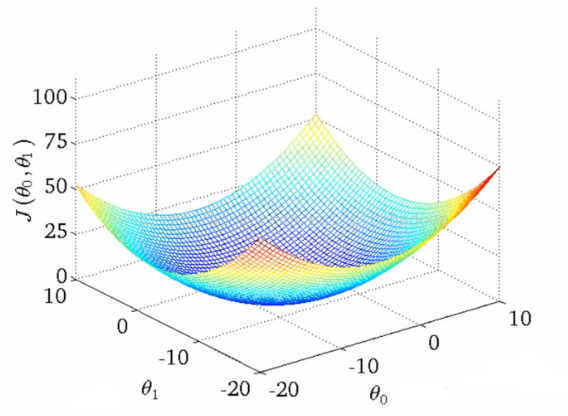
• 我们可以看到，height（y）表示成本函数的值，因此找到y在最小值的位置
  
  
• 我们可以使用轮廓数字/曲线来代替曲面图
  以不同颜色设置椭圆
  每个颜色是相同的J值（θ0，θ1），但是由于θ1和θ0会变化
  想象一下碗状功能从屏幕出来，所以中间是同心圆

• 每个点（像上面的红色）代表Ɵ0和Ɵ1的一对参数值
  我们的例子在这里把参数值如下
  • • θ₀ = ~800
    • θ₁ = ~-0.15
  • 不合适
    • 这些参数给出了远离中心的轮廓图上的值
  • If we have
    • θ₀ = ~360
    • θ₁ = 0
    • 这给了一个更好的假设，但仍然不是很大 - 不是在countour情节的中心 
  • 最后我们找到最小值，给出最佳假设
• 我们真正想要的是找到θ0和θ1的最小值的有效算法

梯度下降算法

• 最小化成本函数J
• 梯度下降
  • 被用于所有的机器学习最小化算法
• 首先查看一般的J（）函数
• 解体思路
  
  • 我们有函数 J(θ₀, θ₁)
  • 希望得到最小化的函数 min J(θ₀, θ₁)
• 渐变下降适用于更一般的功能
  • J(θ₀, θ₁, θ₂ .... θ_n)
  • min J(θ₀, θ₁, θ₂ .... θ_n)
    

它是如何工作的？

• 从初始猜测开始
  • 从0,0开始（或任何其他值）
  • 保持θ0和θ1有一点改变，试图减少J（θ0，θ1）
• 每次更改参数时，选择最大可能减小J（θ0，θ1）的渐变
• 重复上面步骤
• 重复做直到你收敛到当地的最低点
• 但是问题又来了
  • 你在哪里可以确定你最终的最低限度？

• • 这里我们可以看到一个初始化点导致一个局部最小值
  • 另一个不同的开始点导致了另一个局部最小值

正式的定义

• 进行以下直到收敛

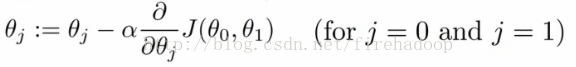
• 这是什么意思？
  • 通过将θj设置为（θj-α）乘以成本函数的偏导数相对于θj来更新θj
• 符号解释
  • :=
    • 表示作业
    • NB a = b 是一个真理断言
  • α (alpha)
    • 是一个叫做学习率的数字参数
    • 控制你每次下降的步伐有多大
      • 如果α大，则具有积极的梯度下降
      • 如果α小，则需要微小的步骤

• 衍生词

• 有一个微妙的关于如何实现这种梯度下降算法
  • Do this for θ₀ and θ₁
  • 对于j = 0和j = 1，意味着我们同时更新两者
  • 我们如何做到这一点？
    • 计算θ0和θ1的右侧
      • 所以我们需要一个临时值
    • 然后，同时更新θ0和θ1
    • 我们以图形方式显示

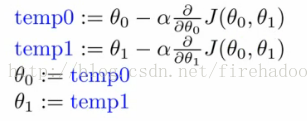
• 如果您实现非同步更新，则它不是梯度下降，并且会出现异常
  但它可能看起来是对的 - 所以重要的是要记住这一点！

了解算法

• 要了解梯度下降，我们将返回一个更简单的函数，我们最小化一个参数来帮助更详细地解释算法
  • min θ₁ J（θ1）其中θ1是实数
• 算法中的两个关键术语
  • Alpha
  • Derivative term
• 符号细微差别
  • 部分Derivative
    • 当我们有多个变量但是只相对于一个变量导出时，使用偏导数
    • 当我们相对于所有变量得出时，使用Derivative
• Derivative term

• • Derivative says
    • 让我们在这一点上进行切线，看看线的斜率
      所以向最小（向下）移动会使负数导数变灰，α总是为正，因此将j（θ1）更新为较小的值
      同样，如果我们上升一个斜率，我们使j（θ1）更大的数字
• Alpha term (α)
  • 如果alpha太小或太大，会发生什么
    太小
    采取婴儿步伐
    时间太久
    太大了
    算法可能超过最小值，不能收敛
• 当你达到当地的最低限度
  • 
    
  切线/导数梯度为0

• So derivative term = 0
  • alpha * 0 = 0
  • So θ₁ = θ₁- 0 
  • So θ₁ remains the same

• 当您接近全局最小值时，导数项变小，所以即使alpha固定，您的更新也会变小
  随着算法的运行，当您接近最小值时，您将采取较小的步骤
  所以不需要随着时间的推移来改变alpha

梯度下降的线性回归

• 应用梯度下降来最小化平方误差成本函数J（θ0，θ1）
  现在我们有一个偏导数

• 这里我们只是扩展第一个表达式
  • J(θ₀, θ₁) = 1/2m....
  • h_θ(x) = θ₀ + θ₁*x
• 我们需要确定每个参数的导数，即
  • When j = 0
  • When j = 1
• 找出θ0和θ1情况下的偏导数
  • 当我们根据j = 0和j = 1导出这个表达式时，我们得到以下结果

• 要检查这个，你需要知道多变量微积分
  所以我们可以将这些值重新插入梯度下降算法
  它是如何工作的
  满足不同局部最优的风险
  线性回归成本函数总是一个凸函数 - 总是有一个最小值
  碗形
  一个全球最佳
  所以梯度下降将总是收敛到全局最优
  在行动
  将值初始化为
• • • • θ₀ = 900
      • θ₁ = -0.1

• 最终达到全局最小值
  这实际上是批量梯度下降
  指的是在每个步骤中，您可以查看所有的培训数据
  每个步骤计算m个训练样例
  有时，非批次版本存在，它们查看小数据子集
  我们将在课程的后面研究其他形式的梯度下降（当m太大时使用）
  存在用于找到最小函数的解的数值解
  
  渐变下降可以更好地扩展到大型数据集
  用于大量的语境和机器学习

算法的两个扩展

• 1) 数值解的正则方程
  • 为了解决最小化问题，我们可以使用避免梯度下降所使用的迭代方法的数值方法来精确地求解它[min J（θ0，θ1）]
    正则方程法
    有优缺点
    优点
    不再是Alpha术语
    对于一些问题可以快一些
    坏处
    更复杂
    我们在多特征部分的线性回归中讨论正态方程
• 2)我们可以学习更多的维度
  所以可能有其他参数有助于更加准确的分析
  例如 与
• 房子尺寸
  房子年龄
  房子卧室数
  房子楼层数
  x1，x2，x3，x4
  有多个参数变得很难绘制
  不能真正绘制在三维以上
  符号也变得更加复杂
  绕过这个最好的方法是线性代数的符号
  提供符号和一系列可以使用矩阵和向量的事物
  例如 矩阵

• 我们在这里看到这个矩阵显示了我们
  尺寸
  卧室数量
  楼层数
  家庭年龄
• 所有在一个变量
  数字块，将所有数据组织成一个大块
• 向量
  显示为y
  向我们显示价格
• 需要线性代数来获得更复杂的线性回归模型
  线性代数对于制作计算效率高的模型是有好处的（如后所述）
  提供使用大量数据集的好方法
  通常，问题的向量化是常见的优化技术