拓扑排序专题

拓扑排序

一．定义

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序(Topological Sort),是将G中所有顶点排成一个线性序列,使得对图中任意一对顶点u和v,若＜u,v＞∈E(G),则u在线性序列中出现在v之前。通常将这样的线性序列称为满足拓扑次序(Topolgical Order)的序列,简称拓扑序列。

二．算法

1.无前趋的顶点优先:

(1)算法描述：

(a)从网中选择一个入度为零的顶点输出；

(b)删除该顶点及其于该点有关的所有边；

(c)是否还有入度为零的顶点？若有，执行(a)，否则结束。

算法实现

以邻接表为图的存储结构的算法：

a)扫描顶点表，将入度为零的顶点入栈；

b)当栈非空时：

输出栈顶元素v，出栈；

检查v的出边，将每条出边的终端顶点的入度减1，若该顶点入度为0，入栈；

c)当栈空时，若输出的顶点小于顶点数，则说明AOV网有回路，否则拓扑排序完成。

算法实现：

void Graph::Toplogicasort()//top是入度为0的顶点栈的栈顶指针
 
 {
     int top=-1;
     for(int i=0;i<n;i++)  //建立如度为0顶点的链栈
     if (count[i]==0)
      {
          count[i]=top;
          top=i;
      }   
     for(int i=0;i<n;i++)
       if(top==-1)
         {
             cout<<"Network has a cycle"<<endl;
             return;
         }
       else
         {
             int j=top;top=count[top];//入度为0的顶点出栈
             count<<j<<endl;
             Edge<float> *l=NodeTable[j].adj;
             while(l)
              {
                  int k=l,dest;
                  if(--count[k]==0)
                    {
                        count[k]=top;//入度减至0的顶点进栈
                        top=k;
                    } 
                  l=l->link;//取j的下一条出边   
              }    
         }        
 }
 /*通常的拓扑算法要用两个数组，一个用来记录每个顶点的入度，当入度为0，则进栈
   。另一个数组用作栈数组，记录入度为0的顶点。其实当入度为0的顶点进栈以后，count[i]
   ＝0就不再有用，所以可以用count[i]记录栈内下一个入度为0的顶点，top指向栈顶顶点号 */

拓扑排序在算法问题中的应用很普遍，下面举例说明：

一。神经网络(NOIP2003)

【问题背景】

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

【问题描述】

 在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经
元之间至多有一条边相连，下图是一个神经元的例子：

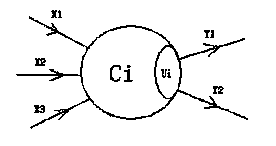
图中，X1—X3是信息输入渠道，Y1－Y2是信息输出渠道，C1表示神经元目前的状态，
Ui是阈值，可视为神经元的一个内在参数。
    神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神
经无分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元
输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

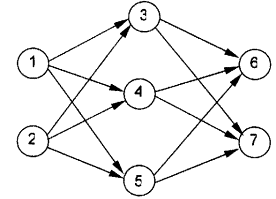
兰兰规定，Ci服从公式：（其中n是网络中所有神经元的数目）

公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒
它会向其他神经元传送信号，信号的强度为Ci。
    如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。
现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网
络输出层的状态。

【输入格式】
输入文件第一行是两个整数n（1≤n≤20）和p。接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。再下面P行，每行由两个整数i，j及一个整数Wij，表示连接神经元i、j的边权值为Wij。

【输出格式】
    输出文件包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状
态，两个整数间以空格分隔。仅输出最后状态非零的输出层神经元状态，并且按照编号由
小到大顺序输出！
    若输出层的神经元最后状态均为 0，则输出 NULL。

【输入样例】
5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1

【输出样例】
3 1
4 1
5 1

本题题目冗长，需要对题目进行转化。
题目中的神经元，可以看作是一个个孤立的结点。每一个传递关系就是一条有向边，起点为输入结点，边指向输出结点。所以神经网络就转化成为一个有向图。
 由于题目规定，结点严格分层，即所有的点严格分成若干个阶段，就好比楼梯，每一个兴奋只能从上面一个阶梯走到下面一个阶梯（即只能从输入层转到输出层）。
 因此，我们可以对结点进行拓扑排序。把每个结点放在相应的阶梯上，这样，递推关系就只能发生在相邻两个阶梯之间。对于递推关系，题目中虽然给出了一个递推公式，但是条件不甚明确，完整的公式应该为：
Cj>0;

这样，题目就转化成了一个简单的图论问题，步骤如下：
1． 拓扑排序，建立起相邻层的递推关系；
2． 递推求解。
例程如下：

#include<iostream>
#include<cstring>
using namespace std;
int w[30][30];
bool a[30][30];//邻接表
int c[30],u[30],f[30],cnt[30];//f,每个结点所在的层；cnt每个结点的入度
int top,n,e;
void toppx()
 {  
     int i,