container-with-most-water（最大蓄水问题）

题目描述:

Given n non-negative integers a1, a2, …, an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container.
（给定n个非负整数a1，a2 ，…，an，其中每个数代表在坐标（i， ai）的一个点。 n条​​垂线被绘制，使得线i的两个端点是在（i， ai ）和（i ，0）。找到两条线，其与X轴一起形成了一个容器，使得所述容器包含最水。
注意：你不能倾斜的容器。）
题目意思就是给一个数组，如[3,4,5,6,8,14,9]，其中的3代表从[1,0]到[1,3]的一条线段，4代表从[2,0]到[2,4]的线段，以此类推，要求求出这些线段中哪两条和x轴一起可以围成一个最大的蓄水池。

解题思路：

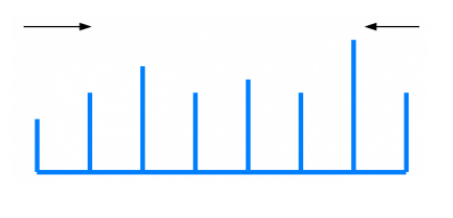
我们假设最初的最大蓄水量为0。然后我们分别从数组的两侧进行扫描，由于不允许倾斜，因此蓄水量仅与较低的那个边有关。因此
$area=min(height[right],height[left])*(right - left )$
如果height[left] < height[right]，那么left右移，找到一个比height[left]大的值。反之，则right左移。同时需要保持跟踪最大值。

AC代码

public class Solution {
    public int maxArea(int[] height) {
        if (height == null | height.length < 2) {
            return 0;
        }

        //max 为最大蓄水面积 left right分别为坐标轴上两侧点
        int max = 0;
        int left = 0;
        int right = height.length - 1;

        while (left < right) {
            max = Math.max(max, Math.min(height[right], height[left]) * (right - left));
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }

        return max;
    }
}