XGBoost

最新推荐文章于 2023-10-10 11:56:28 发布

FarmerJohn

最新推荐文章于 2023-10-10 11:56:28 发布

阅读量5.8k

点赞数 26

分类专栏：机器学习文章标签： XGBoost

机器学习专栏收录该内容

14 篇文章 10 订阅

订阅专栏

本文借鉴自多篇博客，非原创。

XGBoost是机器学习领域最近几年比较火热的一种十分强大的集成学习方法（系统），全称为eXtreme Gradient Boosting，由大牛陈天奇博士开发（陈天奇，交大ACM班毕业，华盛顿大学计算机博士）。

预备知识

Boosting

Boosting是一类可将弱学习器提升为强学习器的集成学习算法。集成学习主要分为两大类，第一类是以Boosting为代表的串联集成学习器，第二类是以Random Forest和Bagging为代表的并联集成学习器。

Boosting的思想是：先训练处初始基学习器，再根据所得基学习器的变现对训练样本的分布进行调整，使得先前在基学习器中做错的样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器；如此往复进行，直到基学习器数目达到约定好的数目，最终将所有的基学习器进行加权结合。

Boosting中有名的成员包括：AdaBoost，GradientBoosting，和LPBoost等。

Gradient Boosting

这部分内容摘自：一步一步理解GB、GBDT、xgboost

对于Boosting，一般基于这样的迭代优化：

$F_{m+1}(x)=F_m(x)+h_m(x)$

关键在于怎么生成h(x)。如果目标函数是回归问题的均方误差，很容易想到最理想的h(x)应该是能够完全拟合 $y-F_m(x)$ ，这就是常说基于残差的学习。残差学习在回归问题中可以很好的使用，但是为了一般性（分类，排序问题），实际中往往是基于loss Function 在函数空间的的负梯度学习，对于回归问题 $(y-F(x))^2$ ，残差和负梯度也是相同的。基于Loss Function函数空间的负梯度的学习也称为“伪残差”。

GB算法的步骤：

GBDT

这部分内容摘自：一步一步理解GB、GBDT、xgboost

关于GBDT（Gradient Boosting Decision Tree）还可参考：GBDT

GB算法中最典型的基学习器是决策树，尤其是CART，正如名字的含义，GBDT（Gradient Boosting Decision Tree）是GB和DT的结合。要注意的是这里的决策树是回归树，GBDT中的决策树是个弱模型，深度较小一般不会超过5，叶子节点的数量也不会超过10，对于生成的每棵决策树乘上比较小的缩减系数（学习率<0.1），有些GBDT的实现加入了随机抽样（subsample 0.5<=f <=0.8）提高模型的泛化能力。通过交叉验证的方法选择最优的参数。因此GBDT实际的核心问题变成怎么基于 $\{(x_i,r_{im})\}_{i=1}^m$ 使用CART回归树生成h(x)。

CART分类树在很多书籍和资料中介绍比较多，但是再次强调GDBT中使用的是回归树。作为对比，先说分类树，我们知道CART是二叉树，CART分类树在每次分枝时，是穷举每一个feature的每一个阈值，根据GINI系数找到使不纯性降低最大的的feature以及其阀值，然后按照feature<=阈值，和feature>阈值分成的两个分枝，每个分支包含符合分支条件的样本。用同样方法继续分枝直到该分支下的所有样本都属于统一类别，或达到预设的终止条件，若最终叶子节点中的类别不唯一，则以多数人的类别作为该叶子节点的性别。回归树总体流程也是类似，不过在每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是GINI系数，而是最小化均方差--即（每个人的年龄-预测年龄）^2 的总和 / N，或者说是每个人的预测误差平方和除以 N。这很好理解，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。分枝直到每个叶子节点上人的年龄都唯一（这太难了）或者达到预设的终止条件（如叶子个数上限），若最终叶子节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。

XGBoost

GBDT是一种基于集成思想下的Boosting学习器，并采用梯度提升的方法进行每一轮的迭代最终组建出强学习器，这样的话算法的运行往往要生成一定数量的树才能达到令我们满意的准确率。当数据集大且较为复杂时，运行一次极有可能需要几千次的迭代运算，这将对我们使用算法造成巨大的计算瓶颈。

虽然GBDT无论在理论推导还是在应用场景实践都是相当完美的，但有一个问题：第n颗树训练时，需要用到第n-1颗树的（近似）残差。从这个角度来看，GBDT比较难以实现分布式，XGBoost正是解决了这个难题。XGBoost是GBDT的高效实现，XGBoost中的基学习器除了可以是CART（GBTree）也可以是线性分类器（GBLinear）。

XGBoost最大的特点在于它能够自动利用CPU的多线程进行并行计算，同时在算法上加以改进提高了精度。在Kaggle的希格斯子信号识别竞赛中，XGBoost因为出众的效率与较高的预测准确度在比赛论坛中引起了参赛选手的广泛关注，在1700多支队伍的激烈竞争中占有一席之地。随着它在Kaggle社区知名度的提高，在其他的比赛中也有队伍借助XGBoost夺得第一。

这部分所有的内容来自原始paper。

从GB到XGBoost

(1) XGBoost在目标函数中显示的加上了正则化项，基学习为CART时，正则化项与树的叶子节点的数量T和叶子节点的值有关。

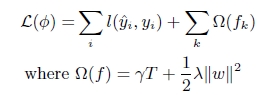
(2) GB中使用Loss Function对f(x)的一阶导数计算出伪残差用于学习生成fm(x)，XGBoost不仅使用到了一阶导数，还使用二阶导数。第t次的loss：

对上式做二阶泰勒展开：g为一阶导数，h为二阶导数

(3) 上面提到CART回归树中寻找最佳分割点的衡量标准是最小化均方差，XGBoost寻找分割点的标准是最大化，lamda，gama与正则化项相关

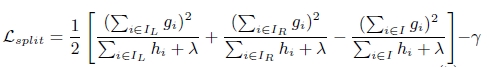
XGBoost算法的步骤和GB基本相同，都是首先初始化为一个常数，GB是根据一阶导数ri，XGBoost是根据一阶导数gi和二阶导数hi，迭代生成基学习器，相加更新学习器。

XGBoost与GBDT除了上述不同，XGBoost在实现时还做了许多优化：

在寻找最佳分割点时，考虑传统的枚举每个特征的所有可能分割点的贪心法效率太低，xgboost实现了一种近似的算法。大致的思想是根据百分位法列举几个可能成为分割点的候选者，然后从候选者中根据上面求分割点的公式计算找出最佳的分割点。
xgboost考虑了训练数据为稀疏值的情况，可以为缺失值或者指定的值指定分支的默认方向，这能大大提升算法的效率，paper提到50倍。
特征列排序后以块的形式存储在内存中，在迭代中可以重复使用；虽然boosting算法迭代必须串行，但是在处理每个特征列时可以做到并行。
按照特征列方式存储能优化寻找最佳的分割点，但是当以行计算梯度数据时会导致内存的不连续访问，严重时会导致cache miss，降低算法效率。paper中提到，可先将数据收集到线程内部的buffer，然后再计算，提高算法的效率。
xgboost 还考虑了当数据量比较大，内存不够时怎么有效的使用磁盘，主要是结合多线程、数据压缩、分片的方法，尽可能的提高算法的效率。

XGBoost原理

目标函数：损失与正则

在监督学习中，我们通常会构造一个目标函数和一个预测函数，使用训练样本对目标函数最小化学习到相关的参数，然后用预测函数和训练样本得到的参数来对未知的样本进行分类的标注或者数值的预测。在XGBoost中，目标函数的形式为： $Obj(\Theta )=L(\Theta )+\Omega (\Theta )$

$L(\Theta )$ ：损失函数，常用损失函数有：

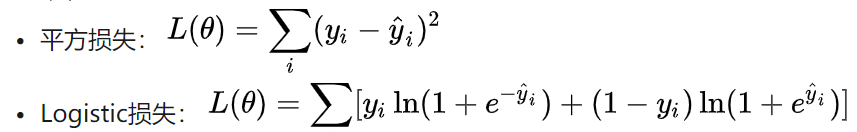
$\Omega (\Theta )$ ：正则化项，之所以要引入它是因为我们的目标是希望生成的模型能准确的预测新的样本（即应用于测试数据集），而不是简单的拟合训练集的结果（这样会导致过拟合）。所以需要在保证模型“简单”的基础上最小化训练误差，这样得到的参数才具有好的泛化性能。而正则项就是用于惩罚复杂模型，避免预测模型过分拟合训练数据，常用的正则有 $L_1$ 正则与 $L_2$ 正则。

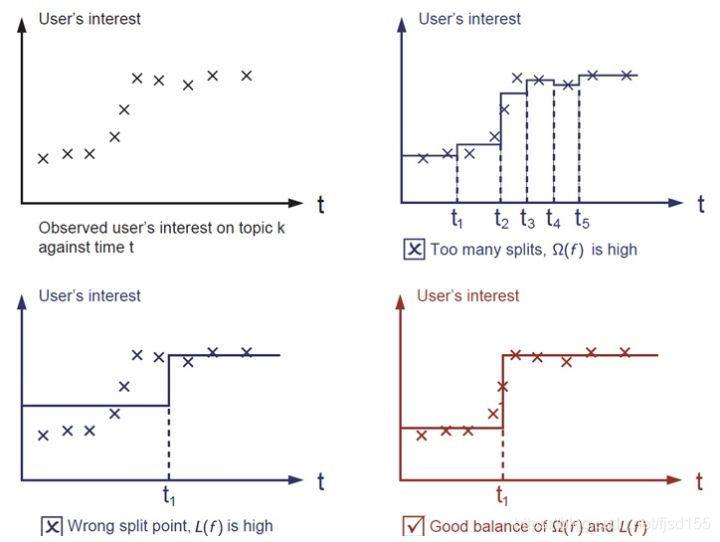
上图所展示的就是损失函数与正则化项在模型中的应用（图片来源：Introduction to Boosted Trees）。观察发现，如果目标函数中的损失函数权重过高，那么模型的预测精度则不尽人意，反之如果正则项的权重过高，所生成的模型则会出现过拟合情况，难以对新的数据集做出有效预测。只有平衡好两者之间的关系，控制好模型复杂度，并在此基础上对参数进行求解，生成的模型才会“简单有效”（这也是机器学习中的偏差方差均衡）。

XGBoost的推导过程

1. 目标函数的迭代与泰勒展开

由于之前已经学习过树的生成及集成方法，这里不再赘述。首先，我们可以把某一次迭代后集成的模型表示为：

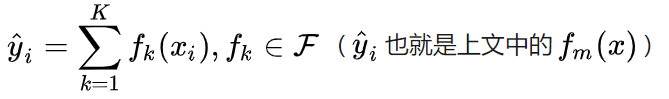
相对应的目标函数：

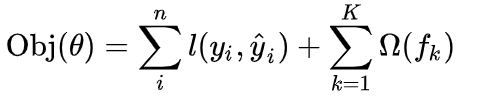
将这两个公式进行扩展，应用在前 t 轮的模型迭代中，具体表示为：

$\hat{y_i}^{t-1}$ 就是前 t-1 轮的模型预测， $f_t(x_i)$ 为新 t 轮加入的预测函数。

这里自然就涉及一个问题：如何选择在每一轮中加入的 $f(x_i)$ 呢？答案很直接，选取的 $f(x_i)$ 必须使得我们的目标函数尽量最大地降低（这里应用到了Boosting的基本思想，即当前的基学习器重点关注以前所有学习器犯错误的那些数据样本，以此来达到提升的效果）。先对目标函数进行改写，表示如下：

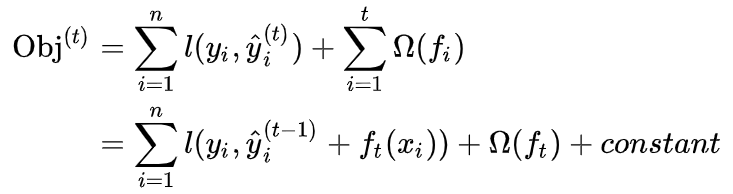
如果我们考虑使用平方误差作为损失函数，公式可改写为：

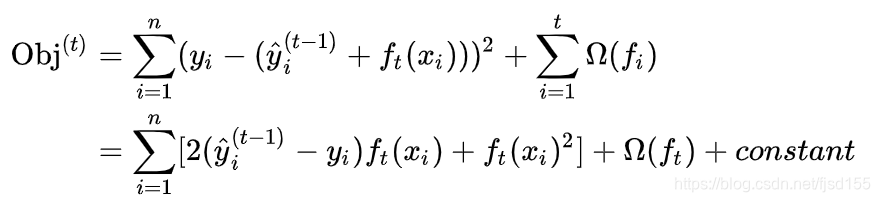
更加一般的，对于不是平方误差的情况，我们可以采用如下的泰勒展开近似来定义一个近似的目标函数，方便我们进行这一步的计算。

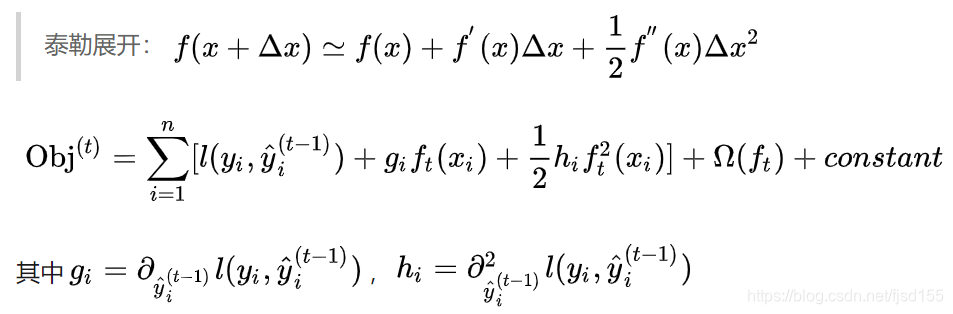
如果移除掉常数项，我们会发现这个目标函数有一个非常明显的特点，它只依赖于每个数据点的在误差函数上的一阶导数和二阶导数（）。有人可能会问，这个公式似乎比我们之前学过的决策树学习难懂。为什么要花这么多力气来做推导呢？
这是因为，这样做会使我们可以很清楚地理解整个目标是什么，并且一步一步推导出如何进行树的学习。这一个抽象的形式对于实现机器学习工具也是非常有帮助的。因为它包含所有可以求导的目标函数，也就是说有了这个形式，我们写出来的代码可以用来求解包括回归，分类和排序的各种问题，正式的推导可以使得机器学习的工具更加一般化。

2. 决策树的复杂度

接着来讨论如何定义树的复杂度。我们先对于 $f$ 的定义做一下细化，把树拆分成结构部分 $q$ 和叶子权重部分 $w$ 。其中结构函数 $q$ 把输入映射到叶子的索引号上面去，而 $w$ 给定了每个索引号对应的叶子分数是什么。具体公式为：

当我们给定上述定义后，那么一棵树的复杂度就为：

这个复杂度包含了一棵树里面节点的个数（左侧），以及每个树叶子节点上面输出分数的 $L_2$ 模平方（右侧）。当然这不是唯一的一种定义方式，不过这一定义方式学习出的树效果一般都比较不错。

简单提及一下 $\gamma$ 和 $\lambda$ 两个系数的作用， $\gamma$ 作为叶子节点的系数，使XGBoost在优化目标函数的同时相当于做了预剪枝； $\lambda$ 作为 $L_2$ 平方模的系数也是要起到防止过拟合的作用。

这里举一个小例子加深对复杂度的理解（图片来源：Introduction to Boosted Trees，下同）

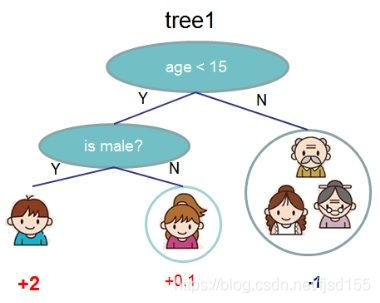
上图为实际生成的一棵决策树，底部的数字代表决策树的预测值，那么这棵树的复杂度自然就为：

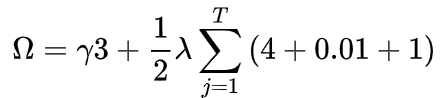
3. 目标函数的最小化

接下来就是非常关键的一步，在这种新的定义下，我们可以把目标函数进行如下改写，其中 $I$ 被定义为每个叶子上面样本集合 $I_j=\left \{ i|q(x_i)=j \right \}$

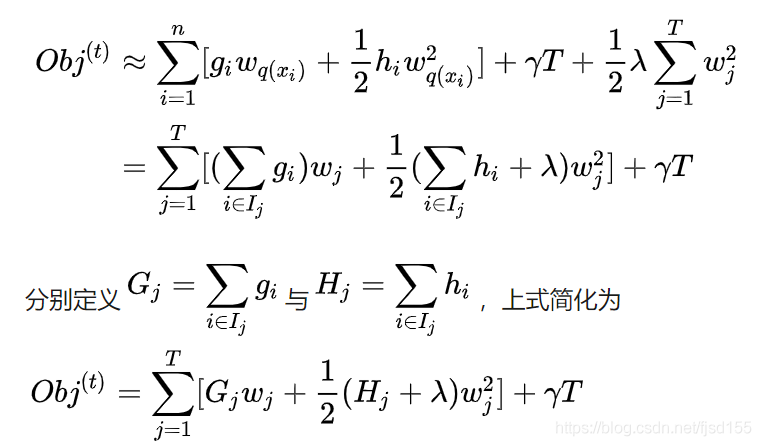
由此，我们将目标函数转换为一个一元二次方程求最小值的问题（在此式中，变量为 $w_j$ ，函数本质上是关于 $w_j$ 的二次函数），略去求解步骤，最终结果如下所示：

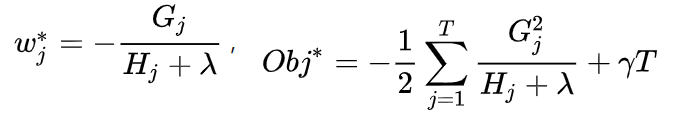
乍一看目标函数的计算与树的结构函数 $q$ 没有什么关系，但是如果我们仔细回看目标函数的构成，就会发现其中 $G_j$ 和 $H_j$ 的取值都是由第 $j$ 个树叶上数据样本所决定的。而第 $j$ 个树叶上所具有的数据样本则是由树结构函数 $q$ 决定的。也就是说，一旦树的结构 $q$ 确定，那么相应的目标函数就能够根据上式计算出来。那么树的生成问题也就转换为找到一个最优的树结构 $q$ ，使得它具有最小的目标函数。

计算求得的 Obj 代表了当指定一个树的结构的时候，目标函数上面最多减少多少。所有我们可以把它叫做结构分数(structure score)。

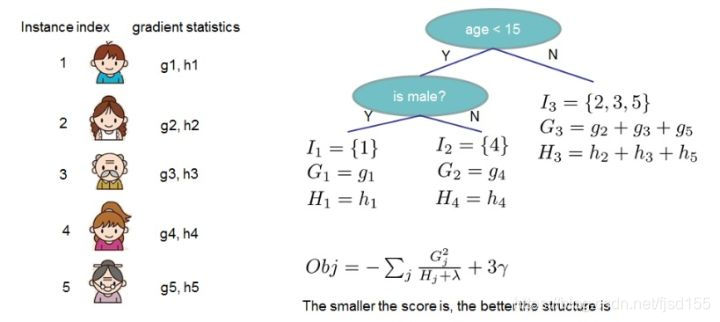
上图为结构分数的一次实际应用，根据决策树的预测结果得到各样本的梯度数据，然后计算出实际的结构分数。正如图中所言，分数越小，代表树的结构越优。

4. 枚举树的结构——贪心法

在前面分析的基础上，当寻找到最优的树结构时，我们可以不断地枚举不同树的结构，利用这个打分函数来寻找出一个最优结构的树，加入到我们的模型中，然后再重复这样的操作。不过枚举所有树结构这个操作不太可行，在这里XGBoost采用了常用的贪心法，即每一次尝试去对已有的叶子加入一个分割。对于一个具体的分割方案，我们可以获得的增益可以由如下公式计算得到：

对于每次扩展，我们还是要枚举所有可能的分割方案，那么如何高效地枚举所有的分割呢？假设需要枚举所有 $x<a$ 这样的条件，那么对于某个特定的分割 $a$ 我们要计算 $a$ 左边和右边的导数和，在实际应用中如下图所示：

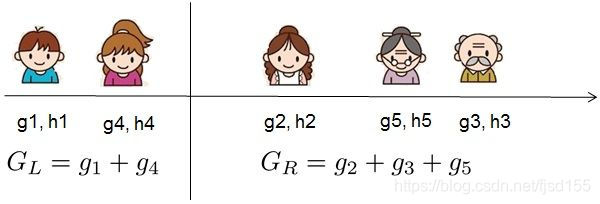
我们可以发现对于所有的 $a$ ，我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度与 $G_L$ 和 $G_R$ 。然后用上面的公式计算每个分割方案的分数就可以了。

但需要注意是：引入的分割不一定会使得情况变好，因为在引入分割的同时也引入新叶子的惩罚项。所以通常需要设定一个阈值，如果引入的分割带来的增益小于一个阀值的时候，我们可以剪掉这个分割。此外在XGBoost的具体实践中，通常会设置树的深度来控制树的复杂度，避免单个树过于复杂带来的过拟合问题。

到这里为止，XGBoost的数学推导就简要介绍完毕。

XGBoost的优良特性

同样是梯度提升，同样是集成学习，那么XGBoost比GBDT要好在哪里呢？结合前面的推导过程与相关博客文章，可大致总结为以下几点：

GBDT是以CART为基分类器，但XGBoost在此基础上还支持线性分类器，此时XGBoost相当于带 $L_1$ 和 $L_2$ 正则化项的Logistics回归（分类问题）或者线性回归（回归问题）
XGBoost在目标函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数和每棵树叶子节点上面输出分数的 $L_2$ 模平方。从偏差方差权衡的角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合
传统的GBDT在优化时只用到一阶导数，XGBoost则对目标函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。（顺便提一下，XGBoost工具支持自定义代价函数，只要函数可一阶和二阶求导）
树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以XGBoost采用了一种近似的算法。大致的思想是根据百分位法列举几个可能成为分割点的候选者，然后从候选者中根据上面求分割点的公式计算找出最佳的分割点
Shrinkage（缩减），相当于学习速率（XGBoost中的eta）。XGBoost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。（当然普通的GBDT实现也有学习速率）
特征列排序后以块的形式存储在内存中，在迭代中可以重复使用；虽然boosting算法迭代必须串行，但是在处理每个特征列时可以做到并行
列抽样（column subsampling）：XGBoost借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是XGBoost异于传统GBDT的一个特性
除此之外，XGBoost还考虑了当数据量比较大，内存不够时怎么有效的使用磁盘，主要是结合多线程、数据压缩、分片的方法，尽可能的提高算法效率

XGBoost参数

（待完善）

XGBoost调参

XGBoost的参数过多，这里推荐三种思路

（1）GridSearch

（2）Hyperopt

（3）老外写的一篇文章，操作性比较强，推荐学习一下。地址

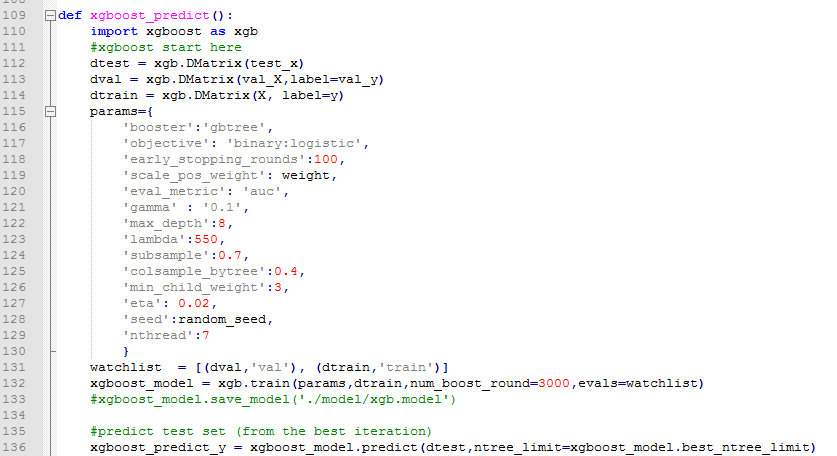
XGBoost代码示例

python中使用XGBoost示例

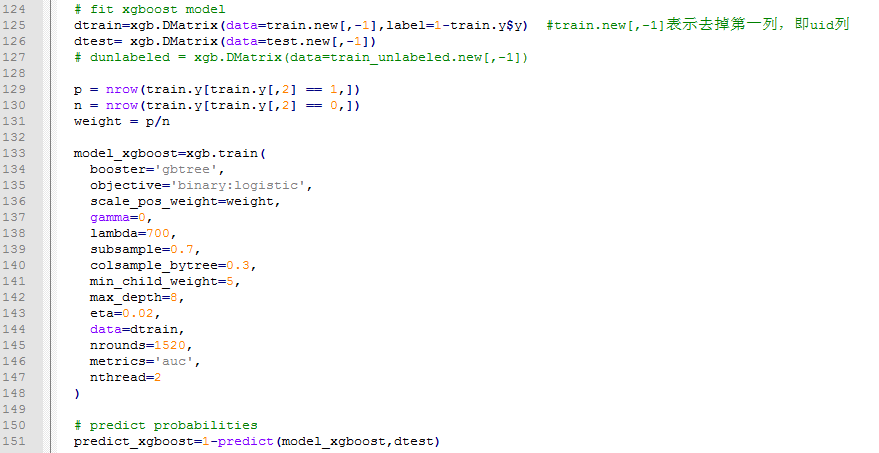
R语言中使用XGBoost示例

示例1：

示例2：

在包中有一组蘑菇数据集可供使用，我们的目标是预测蘑菇是否可以食用（分类任务），此数据集已被分割成训练数据与测试数据。

# xgboost包在安装时需要把R升级到3.3.0以上的版本,否则安装不成功
> install.packages('xgboost')
# 也可使用devtools包安装github版本
> devtools::install_github('dmlc/xgboost', subdir='R-package')
> library(xgboost)

> data(agaricus.train, package='xgboost')
> data(agaricus.test, package='xgboost')
> train <- agaricus.train 
> test <- agaricus.test

# 整个数据集是由data和label组成的list
> class(train)
[1] "list"
# 查看数据维度
> dim(train$data)
[1] 6513  126
> dim(test$data)
[1] 1611  126

# 在此数据集中，data是一个dgCMatrix类的稀疏矩阵,label是一个由{0,1}构成的数值型向量
> str(train)
List of 2
 $ data :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
  .. ..@ i       : int [1:143286] 2 6 8 11 18 20 21 24 28 32 ...
  .. ..@ p       : int [1:127] 0 369 372 3306 5845 6489 6513 8380 8384 10991 ...
  .. ..@ Dim     : int [1:2] 6513 126
  .. ..@ Dimnames:List of 2
  .. .. ..$ : NULL
  .. .. ..$ : chr [1:126] "cap-shape=bell" "cap-shape=conical" "cap-shape=convex" "cap-shape=flat" ...
  .. ..@ x       : num [1:143286] 1 1 1 1 1 1 1 1 1 1 ...
  .. ..@ factors : list()
 $ label: num [1:6513] 1 0 0 1 0 0 0 1 0 0 ...

xgboost包提供了两个函数用于模型构建，分别是xgboost()与xgb.train()，前者可以满足对算法参数的基本设置，而后者的话在此基础上可以实现一些更为高级的功能。

# data与label分别指定数据与标签
# max.deph：树的深度,默认值为6,在此数据集中的分类问题比较简单，设置为2即可
# nthread：并行运算的CPU的线程数,设置为2;
# nround：生成树的棵数
# objective = "binary:logistic"：设置逻辑回归二分类模型
> xgboost_model <- xgboost(data = train$data, label = train$label, max.depth = 2, eta = 1, nthread = 2, nround = 2, objective = "binary:logistic")
# 得到两次迭代的训练误差
[1]	train-error:0.046522 
[2]	train-error:0.022263

xgboost函数可调用的参数众多，在此不在详细展开介绍，可参阅博客文章[译]快速上手：在R中使用XGBoost算法中的"在xgboost中使用参数"一节，该文章将这些参数归为通用、辅助和任务参数三大类，对我们掌握算法与调参有着很大帮助。

# 设置verbose参数,可以显示内部的学习过程
> xgboost_model <- xgboost(data = train$data, label = train$label, 
+ max.depth = 2, eta = 1, nthread = 2, nround = 2, verbose = 2,
+ objective = "binary:logistic")
[13:56:36] amalgamation/../src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 6 extra nodes, 0 pruned nodes, max_depth=2
[1]	train-error:0.046522 
[13:56:36] amalgamation/../src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 4 extra nodes, 0 pruned nodes, max_depth=2
[2]	train-error:0.022263

# 将建立好的模型用于预测新的数据集
> xgboost_pred <- predict(xgboost_model, test$data)
> head(xgboost_pred)
[1] 0.28583017 0.92392391 0.28583017 0.28583017 0.05169873 0.92392391
# 以上给出的是每一个样本的预测概率值,进一步转化后可得到具体的预测分类
> prediction <- as.numeric(xgboost_pred > 0.5)
> head(prediction)
[1] 0 1 0 0 0 1
> model_accuracy <- table(prediction,test$label)
> model_accuracy
          
prediction   0   1
         0 813  13
         1  22 763
> model_accuracy_1 <- sum(diag(model_accuracy))/sum(model_accuracy)
> model_accuracy_1
[1] 0.9782744

高级功能

xgb.train()函数可以实现一些高级功能，帮助我们对模型进行进一步的优化。

# 在使用函数前需要将数据集进行转换为xgb.Dmatrix格式
> dtrain <- xgb.DMatrix(data = train$data, label=train$label)
> dtest <- xgb.DMatrix(data = test$data, label=test$label)

# 使用watchlist参数,可同时得到训练数据与测试数据的误差
> watchlist <- list(train=dtrain, test=dtest)
> xgboost_model <- xgb.train(data=dtrain, max.depth=2, eta=1, nthread = 2,
+ nround = 3,objective = "binary:logistic",watchlist = watchlist)
[1]	train-error:0.046522	test-error:0.042831 
[2]	train-error:0.022263	test-error:0.021726
[3]	train-error:0.007063	test-error:0.006207

# 自定义损失函数,可同时观察两种损失函数的表现
# eval.metric可使用的参数包括'logloss'、'error'、'rmse'等
> xgboost_model <- xgb.train(data=dtrain, max.depth=2, eta=1, nthread = 2,
+ nround=3, watchlist=watchlist, eval.metric = "error", 
+ eval.metric = "logloss", objective = "binary:logistic")
[1]	train-error:0.046522	train-logloss:0.233376	test-error:0.042831	test-logloss:0.226686 
[2]	train-error:0.022263	train-logloss:0.136658	test-error:0.021726	test-logloss:0.137874 
[3]	train-error:0.007063	train-logloss:0.082531	test-error:0.006207	test-logloss:0.080461

# 查看特征的重要性,方便我们在模型优化时进行特征筛选
> importance_matrix <- xgb.importance(model = xgboost_model)
> importance_matrix
   Feature       Gain      Cover Frequency
1:      28 0.60036585 0.41841659     0.250
2:      55 0.15214681 0.16140352     0.125
3:      59 0.10936624 0.13772146     0.125
4:     101 0.04843973 0.07979724     0.125
5:     110 0.03391602 0.04120512     0.125
6:      66 0.02973248 0.03859211     0.125
7:     108 0.02603288 0.12286396     0.125
# 使用xgb.plot.importance()函数进行可视化展示
> xgb.plot.importance(importance_matrix)

# 使用xgb.dump()查看模型的树结构
> xgb.dump(xgboost_model,with_stats = T)
 [1] "booster[0]"                                                            
 [2] "0:[f28<-9.53674e-007] yes=1,no=2,missing=1,gain=4000.53,cover=1628.25" 
 [3] "1:[f55<-9.53674e-007] yes=3,no=4,missing=3,gain=1158.21,cover=924.5"   
 [4] "3:leaf=0.513653,cover=812"                                             
 [5] "4:leaf=-0.510132,cover=112.5"                                          
 [6] "2:[f108<-9.53674e-007] yes=5,no=6,missing=5,gain=198.174,cover=703.75" 
 [7] "5:leaf=-0.582213,cover=690.5"                                          
 [8] "6:leaf=0.557895,cover=13.25"
 ---
# 将上述结果通过树形结构图表达出来 
> xgb.plot.tree(model = xgboost_model)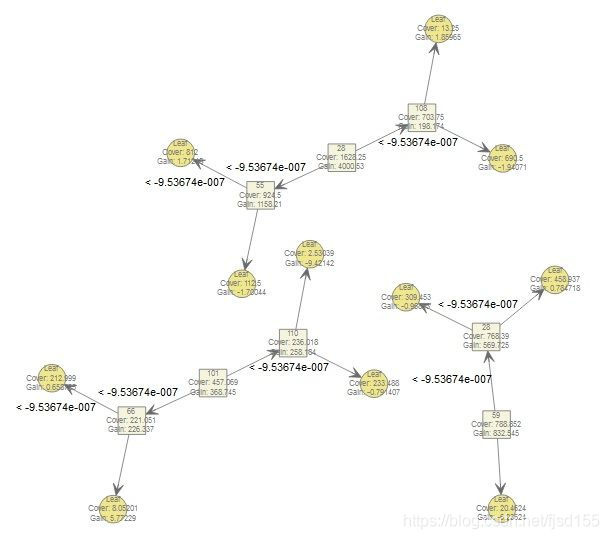

DART

核心思想就是将dropout引入XGBoost。（待完善）

参考资料

陈天奇博士的PPT

XGBoost导读和实战

一步一步理解GB、GBDT、xgboost

xgboost原理

梯度提升树GBDT原理

XGBoost Tutorials

机器学习算法中 GBDT 和 XGBOOST 的区别有哪些

XGBoost的github地址

自定义目标函数

DART

XGBoost: A Scalable Tree Boosting System

XGBoost: Reliable Large-scale Tree Boosting System

XGBoost 论文翻译+个人注释

Story and lessons behind the evolution of xgboost

Boosted Tree：一篇很有见识的文章

xgboost的原理没你想像的那么难

一文读懂机器学习大杀器XGBoost原理

COS 访谈第 18 期：陈天奇

Learn R | GBDT of Data Mining（三）

Learn R | GBDT of Data Mining（四）

Get Started with XGBoost

严酷的魔王：xgboost：速度快效果好的boosting模型 | 统计之都

xgboost：速度快效果好的Boosting模型

机器学习算法中GBDT和XGBOOST的区别有哪些？ - 知乎

[译]快速上手：在R中使用XGBoost算法 - FinanceR

FarmerJohn

关注

26
点赞
踩
195

收藏

觉得还不错? 一键收藏
0
评论
XGBoost

本文借鉴自多篇博客，非原创。XGBoost是机器学习领域最近几年比较火热的一种十分强大的集成学习方法（系统），全称为eXtreme Gradient Boosting，由大牛陈天奇博士开发（陈天奇，交大ACM班毕业，华盛顿大学计算机博士）。预备知识BoostingBoosting是一类可将弱学习器提升为强学习器的集成学习算法。集成学习主要分为两大类，第一类是以Boosting...
复制链接

扫一扫