LeetCode 307. Range Sum Query - Mutable

分析

难度 中
来源 https://leetcode.com/problems/range-sum-query-mutable/
思路
使用树状数组（Binary Indexed Tree）

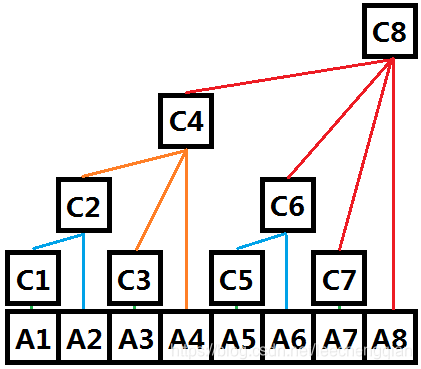
其中A为普通数组，C为树状数组，奇数下标一定是叶子结点。
相比线段树，所用空间更小，速度更快，但节点数据需要可加减。

题目

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:

1. The array is only modifiable by the update function.
2. You may assume the number of calls to update and sumRange function is distributed evenly.

解答

Runtime: 56 ms, faster than 98.72% of Java online submissions for Range Sum Query - Mutable.
Memory Usage: 47.7 MB, less than 86.26% of Java online submissions for Range Sum Query - Mutable.

package LeetCode;
/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * obj.update(i,val);
 * int param_2 = obj.sumRange(i,j);
 */
public class L307_RangeSumQuery_Mutable {
    private void printNumArray(int[] nums){
        for(int i=0;i<nums.length;i++){
            System.out.print(nums[i]+"\t");
        }
        System.out.println();
    }

    private int[] presum;//树状数组
    private int[] nums;
    int n;
    int lowbit(int x) {//返回参数转为二进制后,最后一个1的位置所代表的数值
        return x & (-x);
    }
    public L307_RangeSumQuery_Mutable(int[] nums) {
        this.nums=nums;
        this.n=nums.length;
        presum=new int[n];
        for(int i=0;i<n;i++)//
        {
            int temp=(lowbit(i+1))/2;
            while(temp>0){
                presum[i]+=presum[i-temp];
                temp/=2;
            }
            presum[i]+=nums[i];
        }
    }

    public void update(int i, int val) {//只影响比自己高级的。
        int diff=val-nums[i];//表示现值比原值的增长，所以下边为加。
        nums[i]=val;
        presum[i]+=diff;
        int jump=lowbit(i+1);
        while(i+jump<n){
            i+=jump;//i+jump至少与i处于同一层。
            presum[i]+=diff;
            jump=lowbit(i+1);
        }
    }

    private int sum(int m){//获取到m的和。
        int sum=0;
        while(m>=0){
            sum+=presum[m];
            m-=lowbit(m+1);//只往回加比m高阶的（低阶的数值已经包含在高阶的内部了）
        }
        return sum;
    }
    public int sumRange(int i, int j) {
        if(j>nums.length-1)
            return -1;
        if(i>0)
            return sum(j)-sum(i-1);
        else
            return sum(j);
    }

    public static void main(String[] args){
        //输入["NumArray","update","update","update","sumRange","update","sumRange","update","sumRange","sumRange","update"]
        //输入[[[7,2,7,2,0]],[4,6],[0,2],[0,9],[4,4],[3,8],[0,4],[4,1],[0,3],[0,4],[0,4]]
        //预期结果[null,null,null,null,6,null,32,null,26,27,null]

       /* int[] nums={7,2,7,2,0};
        L307_RangeSumQuery_Mutable l307=new L307_RangeSumQuery_Mutable(nums);
        l307.update(4,6);
        l307.update(0,2);
        l307.update(0,9);
        System.out.println(l307.sumRange(4,4));
        l307.update(3,8);
        System.out.println(l307.sumRange(0,4));
        l307.update(4,1);
        System.out.println(l307.sumRange(0,3));
        System.out.println(l307.sumRange(0,4));
        l307.update(0,4);*/

       /*
        Input
        ["NumArray",                            "sumRange","update","sumRange","update","update",   "update",   "sumRange","sumRange",  "update",   "update"]
        [[[41,-53,-11,-58,94,-18,-80,10,-98,-3]],[5,6],     [1,77], [0,3],      [5,21], [0,-45],    [8,6],      [7,7],      [9,9],      [4,70],     [5,61]]
        Output
        [null,-98,null,49,null,null,null,96,-89,null,null]
        Expected
        [null,-98,null,49,null,null,null,10,-3,null,null]
        */
        int[] nums={41,-53,-11,-58,94,-18,-80,10,-98,-3};
        L307_RangeSumQuery_Mutable l307=new L307_RangeSumQuery_Mutable(nums);

        System.out.println(l307.sumRange(5,6));
        l307.update(1,77);
        System.out.println(l307.sumRange(0,3));
        l307.update(5,21);
        l307.update(0,-45);
        l307.update(8,6);
        l307.sum(7);
        System.out.println(l307.sumRange(7,7));
        System.out.println(l307.sumRange(9,9));
        l307.update(4,70);
        l307.update(5,61);
    }
}