文章目录
1 条件随机场定义
1.1 马尔科夫随机场
1.1.1 用图模型表示概率
图G=(V,E),V表示顶点集合,E表示边的集合。
概率图模型表示用图表示概率的分布。
可以用无向图G表示联合概率分布P(Y)。Y一定是一个矢量。
顶点
v
∈
V
v \in V
v∈V表示一个随机变量
Y
v
Y_v
Yv,
Y
=
(
Y
v
)
v
∈
V
Y = (Y_v)_{v \in V}
Y=(Yv)v∈V。
边
e
∈
E
e \in E
e∈E表示随机变量之间的概率依赖关系。
这样对联合概率分布的计算转为对无向图的计算。联合概率分布P(Y)需要满足三个马尔科夫性。
1.1.3 三个马尔科夫性
1 成对马尔科夫性
讲的是两个没有边连接的节点,联合概率等于概率的乘积。
假设无向图G中,u和v是两个没有边连接的结点,分别对应随机变量
Y
u
Y_u
Yu,
Y
v
Y_v
Yv。其他所有节点为O,对应随机变量组
Y
O
Y_O
YO。那么:
P
(
Y
u
,
Y
v
∣
Y
O
)
=
P
(
Y
u
∣
Y
O
)
P
(
Y
v
∣
Y
O
)
P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O)
P(Yu,Yv∣YO)=P(Yu∣YO)P(Yv∣YO)
2 局部马尔科夫性
讲的是一个节点和与它没有任何边连接的节点的集合,联合概率等于概率的乘积。
假设无向图G中,v是任意一个结点,对应随机变量
Y
v
Y_v
Yv。W是与v有边连接的所有节点的集合,对应随机变量组
Y
W
Y_W
YW。O是v和W之外的所有节点,对应随机变量组
Y
O
Y_O
YO。那么:
P
(
Y
v
,
Y
O
∣
Y
W
)
=
P
(
Y
v
∣
Y
W
)
P
(
Y
O
∣
Y
W
)
P(Y_v,Y_O|Y_W)=P(Y_v|Y_W)P(Y_O|Y_W)
P(Yv,YO∣YW)=P(Yv∣YW)P(YO∣YW)
3 全局马尔科夫性
讲的是两个集合,一个集合中的任意一个点,与另外一个集合中的任意一个点没有边连接, 那两个集合的联合概率等于概率的乘积。
假设节点集合A、B,是在无向图G中被集合C分开的任意节点的集合,分别对应随机变量组
Y
A
Y_A
YA,
Y
B
Y_B
YB,
Y
C
Y_C
YC。那么:
P
(
Y
A
,
Y
B
∣
Y
C
)
=
P
(
Y
A
∣
Y
C
)
P
(
Y
B
∣
Y
C
)
P(Y_A,Y_B|Y_C)=P(Y_A|Y_C)P(Y_B|Y_C)
P(YA,YB∣YC)=P(YA∣YC)P(YB∣YC)
1.1.3 重点再看局部马尔科夫性
成对马尔科夫性,局部马尔科夫性以及全局马尔科夫性是等价的。
v是无向图G中任意一个结点,对应随机变量
Y
v
Y_v
Yv。
W是与v有边链接的所有结点,对应随机变量组是
Y
W
Y_W
YW。
O是v,W以外的所有结点,对应随机变量组是
Y
O
Y_O
YO。
那么
P
(
Y
v
,
Y
O
∣
Y
W
)
=
P
(
Y
v
∣
Y
W
)
P
(
Y
O
∣
Y
W
)
P(Y_v,Y_O|Y_W) =P(Y_v|Y_W)P(Y_O|Y_W)
P(Yv,YO∣YW)=P(Yv∣YW)P(YO∣YW),说明给定
Y
W
Y_W
YW条件下
Y
v
Y_v
Yv和
Y
O
Y_O
YO是条件独立的。也就是说v只与W有关系。
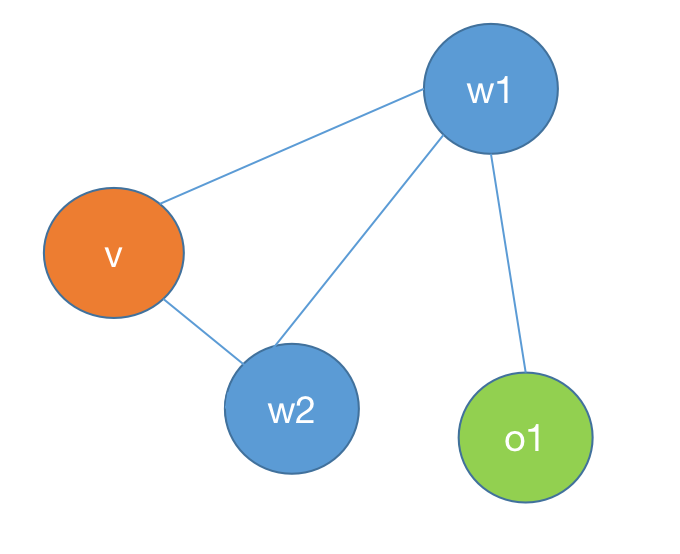
如图所示W表示所有与v相连的点。O表示除v和W之外的所有点。
我们再看 P ( Y v , Y O ∣ Y W ) = P ( Y v ∣ Y O , Y W ) P ( Y O ∣ Y W ) P(Y_v,Y_O|Y_W) =P(Y_v|Y_O,Y_W)P(Y_O|Y_W) P(Yv,YO∣YW)=P(Yv∣YO,YW)P(YO∣YW)(根据条件概率公式)
两个公式联合起来得到结论: P ( Y v ∣ Y W ) = P ( Y v ∣ Y O , Y W ) P(Y_v|Y_W) = P(Y_v|Y_O,Y_W) P(Yv∣YW)=P(Yv∣YO,YW)(记为公式1)
1.2 马尔科夫随机场的因子分解
团:无向图中任意两个结点均有边相连的节点子集。
最⼤团:⽆向图 中的⼀个团,并且不能再加进任何⼀个结点使其成为⼀个更⼤的团。
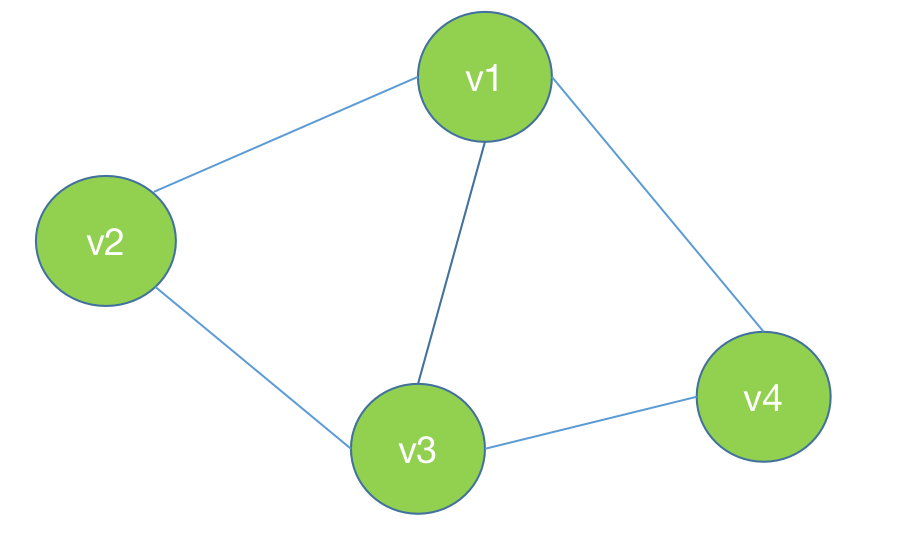
这个图中的最大团是(v1,v2,v3)或者(v1,v3,v4)
概率无向图的联合概率分布
P
(
Y
)
=
1
Z
∏
C
Φ
C
(
Y
C
)
P(Y) = \dfrac{1}{Z}\prod_C \Phi_C(Y_C)
P(Y)=Z1∏CΦC(YC)
(概率无向图的联合概率分布就等于所有最大团的一个累乘,所有最大团上势函数的累乘)
其中C是无向图的最大团,
Y
C
Y_C
YC是C的节点对应的随机变量,
势函数
Φ
C
(
Y
C
)
=
e
x
p
{
−
E
(
Y
C
)
}
\Phi_C(Y_C)=exp\{-E(Y_C)\}
ΦC(YC)=exp{−E(YC)}
Z是规范化因子,是一个全概率分布,
Z
=
∑
Y
∏
C
Φ
C
(
Y
C
)
Z=\sum_Y\prod_C\Phi_C(Y_C)
Z=∑Y∏CΦC(YC)
乘积是在无向图所有的最大图上进行的。
势函数会根据模型的不同而不同。
1.3 条件随机场
设X与Y是随机变量,P(Y|X)是在给定X的条件下Y的条件概率分布。如果Y构成一个由无向图G表示的马尔科夫随机场,则称条件概率分布P(Y|X)为条件随机场。
对于任意v,都有
P
(
Y
v
∣
X
,
Y
w
,
w
≠
v
)
=
P
(
Y
v
∣
X
,
Y
w
,
w
−
v
)
P(Y_v|X,Y_w,w\ne v) = P(Y_v|X,Y_w,w-v)
P(Yv∣X,Yw,w=v)=P(Yv∣X,Yw,w−v) w-v表示w是与v相连的所有点。也就是说v事件发生的概率只与与它相连的点有关系。
说明:X是Y的条件,X是输入,Y是输出。
这个公式的由来是从公式1对比得到的。增加了条件X。
这个公式可以描述为:任意一个节点v的在与它有边相连的条件下的概率,等于非v条件下的概率。
1.4 线性链条件随机场
再进一步约束:我们用无向图G表示事件Y的概率,Y中包含Y1,Y2,Y3…Yn。这些事件之间具有线性关系。
再假设条件X,X包含X1,X2,X3…Xn。X和Y之间具有线性关系。如下图所示。
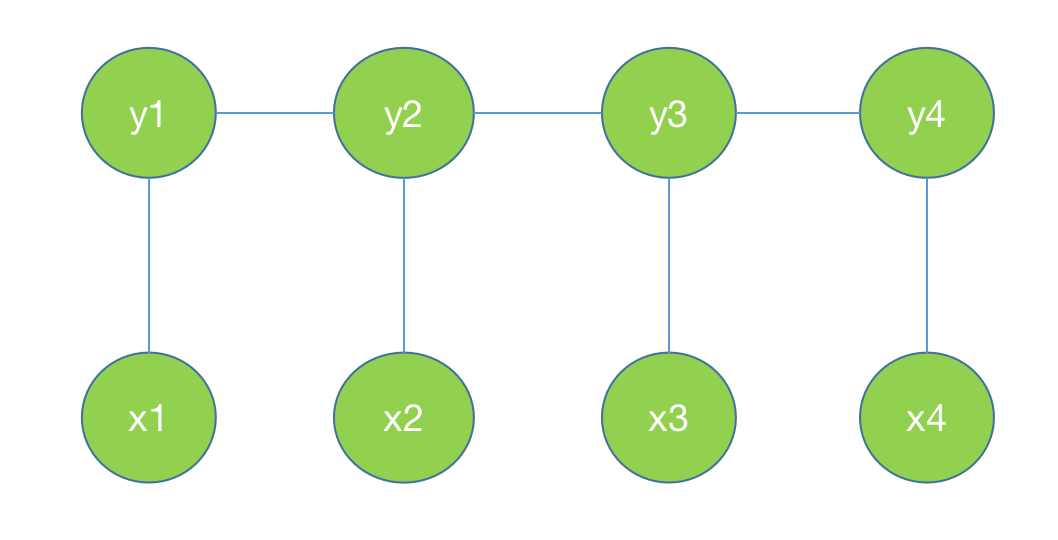
也就是说加上条件Y是具有线性关系的,X和Y具有相同的线性结构。上面的公式可以写为:
P
(
Y
i
∣
X
,
Y
1
,
Y
2
.
.
.
Y
i
−
1
,
Y
i
+
1
,
.
.
.
Y
n
)
=
P
(
Y
i
∣
X
,
Y
i
−
1
,
Y
i
+
1
)
P(Y_i|X,Y_1,Y_2...Y_{i-1},Y_{i+1},...Y_n) = P(Y_i|X,Y_{i-1},Y_{i+1})
P(Yi∣X,Y1,Y2...Yi−1,Yi+1,...Yn)=P(Yi∣X,Yi−1,Yi+1)。这个公式称为线性链条件随机场。记为公式2。
与节点i有边相连的节点时候
i
−
1
i-1
i−1和
i
+
1
i+1
i+1。
不等于i的节点有:1,2,…i-1,i+1,…n
X是条件
2线性链条件随机场的表示形式
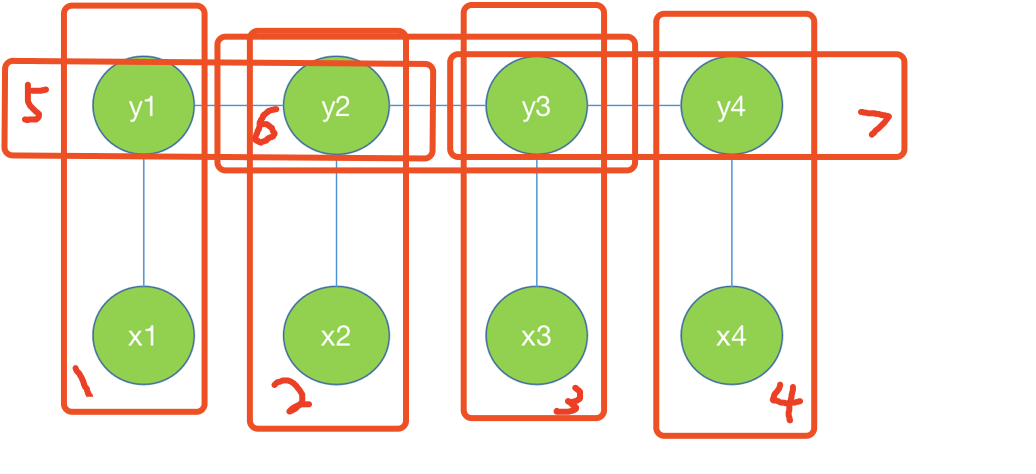
可以看到在图中是有7个最大团。计算P(Y|X)就是所有最大团的势函数的累乘。
2.1 参数化形式
定义了每个节点和每条边的特征函数,用特征函数表示概率。
P
(
Y
)
=
s
1
t
1
s
2
t
2
.
.
.
t
n
−
1
s
n
P(Y)=s_1t_1s_2t_2...t_{n-1}s_n
P(Y)=s1t1s2t2...tn−1sn
设P(Y|X)为线性链条件随机场,则在随机变量X取值为x的条件下,随机变量Y取值为y的条件概率
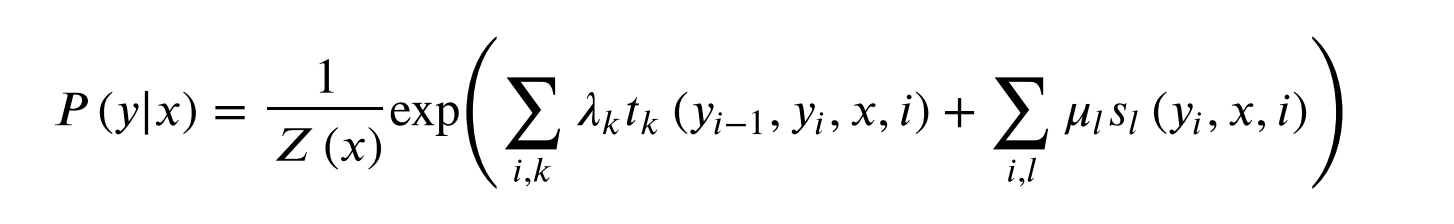
其中,
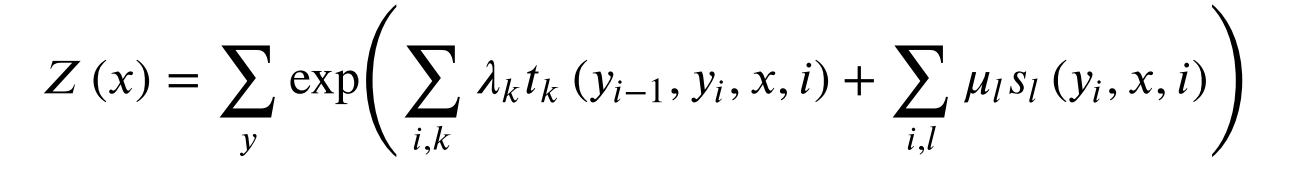
t
k
t_k
tk是定义在边上的特征函数。依赖于当前和前一个位置。
s
l
s_l
sl是定义在结点上的特征函数,称为状态特征,依赖于当前位置。
t
k
t_k
tk和
s
l
s_l
sl值为1或者0。
λ
k
\lambda_k
λk和
μ
l
\mu_l
μl是对应的权值。
Z(x)是规范化因子,求和是在所有可能的输出序列上。
注意:这两句话没理解明白,暂时记录在这里。
s
l
s_l
sl的个数应该等于边的个数 x 每个顶点可能的取值集合个数
t
k
t_k
tk个数=边的个数 x(第一个顶点取值个数 x 第二个顶点取值个数)
这是按照上面最大团的定义来确定的。
2.2 简化形式
用
f
k
f_k
fk表示边的特征函数和节点的特征函数。
设有
K
1
K_1
K1个边的特征函数,有
K
2
K_2
K2个节点的特征函数,
K
=
K
1
+
K
2
K=K_1+K_2
K=K1+K2
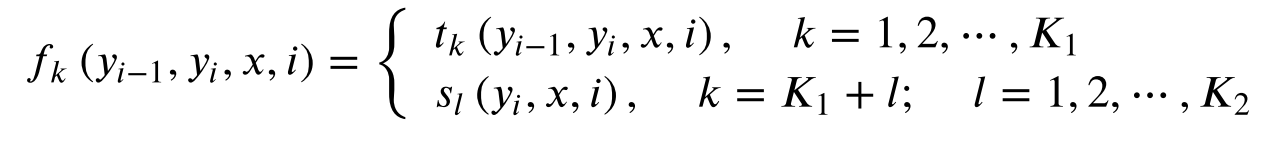
用
w
k
w_k
wk表示边的权重和节点的权重。
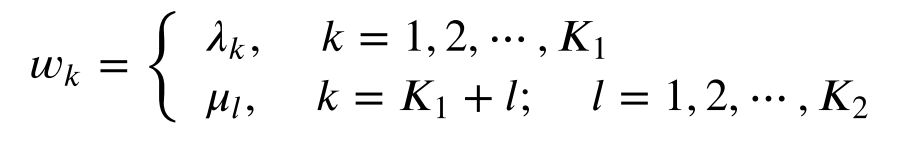
则条件随机场表示为:
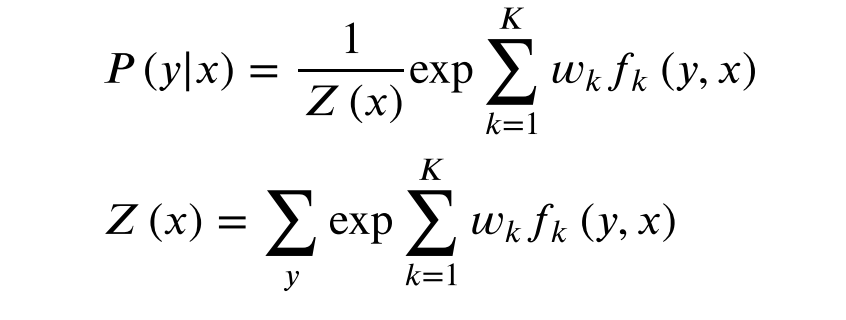
用向量化表示为:
P
(
y
∣
x
)
=
e
x
p
(
w
.
F
(
y
,
x
)
)
Z
w
(
x
)
P(y|x)=\dfrac{exp(w.F(y,x))}{Z_w(x)}
P(y∣x)=Zw(x)exp(w.F(y,x)),其中
Z
w
(
x
)
=
∑
y
e
x
p
(
w
.
F
(
y
,
x
)
)
Z_w(x) = \sum_y exp(w.F(y,x))
Zw(x)=∑yexp(w.F(y,x))
2.3 矩阵形式
引入一个特殊的起点标记
y
0
=
s
t
a
r
t
y_0=start
y0=start表示开始状态,
y
n
+
1
=
s
t
o
p
y_{n+1}=stop
yn+1=stop表示终止状态。定义一个m阶矩阵。
m是
y
i
y_i
yi取值的个数。
如果
y
i
y_i
yi表示骰子出现的某一面,那么m=6;如果
y
i
y_i
yi表示一枚硬件哪面朝上,那么m=2。
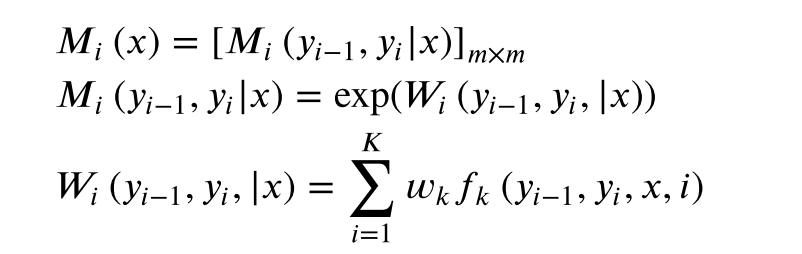
P ( y ∣ x ) = 1 Z w ( x ) ∏ i = 1 n + 1 M i ( y i − 1 , y i ∣ x ) P(y|x) = \dfrac{1}{Z_w(x)}\prod^{n+1}_{i=1}M_i(y_{i-1},y_i|x) P(y∣x)=Zw(x)1∏i=1n+1Mi(yi−1,yi∣x),
其中 Z w ( x ) = ( M 1 ( x ) , M 2 ( x ) , . . . M n + 1 ( x ) ) s t a r t , s t o p Z_w(x)=(M_1(x),M_2(x),...M_{n+1}(x))_{start,stop} Zw(x)=(M1(x),M2(x),...Mn+1(x))start,stop
矩阵最关注矩阵的形状。
3 条件随机场的概率计算
条件随机场的概率计算问题是:计算条件概率 P ( Y i = y i ∣ x ) P(Y_i=y_i|x) P(Yi=yi∣x), P ( Y i − 1 = y i − 1 , Y i = y i ∣ x ) P(Y_{i-1}=y_{i-1},Y_{i}=y_i|x) P(Yi−1=yi−1,Yi=yi∣x) 以及它们的希望。
前向计算
后向计算
计算特征函数
f
k
(
x
,
y
)
f_k(x,y)
fk(x,y)关于条件分布P(Y|X)的数学期望:
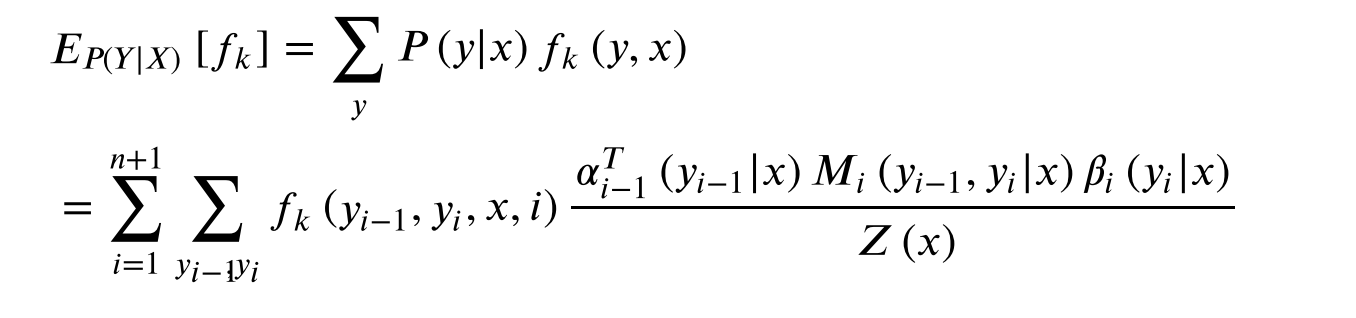
计算特征函数
f
k
(
x
,
y
)
f_k(x,y)
fk(x,y)关于联合分布P(X,Y)的数学期望:
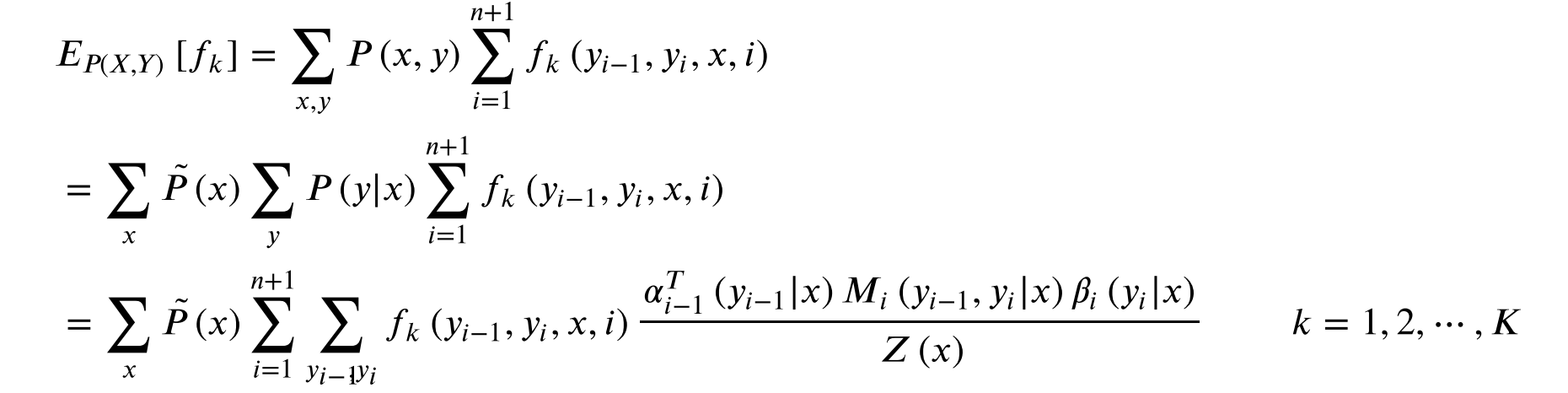
这里的结果是中间量
4 条件随机场的学习算法
4.1 最大熵模型
4.1.1最大熵模型定义
模型就是一个从输入到输出的一个映射,可以是一个f(x),也可以是一个P(y|x)。当在所有条件都满足的时候,这个函数不唯一的时候,就使用最大熵策略来选择模型。所以最大熵模型是一种选择策略,是一种世界观。
熵最大=变量几乎可以均匀分布
假设分类模型是条件概率分布P(Y|X)。给定条件X,以条件概率P(Y|X)输出Y。
给定训练集,可以确定联合分布P(X,Y)的经验分布和边缘分布P(X)的经验分布,分别以
P
^
(
X
,
Y
)
\hat{P}(X,Y)
P^(X,Y)和
P
^
(
X
)
\hat{P}(X)
P^(X)。这里
P
^
(
X
=
x
,
Y
=
y
)
=
v
(
X
=
x
,
Y
=
y
)
N
\hat{P}(X=x,Y=y)=\dfrac{v(X=x,Y=y)}{N}
P^(X=x,Y=y)=Nv(X=x,Y=y)
P
^
(
X
=
x
)
=
v
(
X
=
x
)
N
\hat{P}(X=x)=\dfrac{v(X=x)}{N}
P^(X=x)=Nv(X=x)
其中, v ( X = x , Y = y ) v(X=x,Y=y) v(X=x,Y=y)表示训练样本中(x,y)出现的频率, v ( X = x ) v(X=x) v(X=x)表示训练样本中x出现的频率。N表示样本容量。
特征函数f(x,y)描述输入x和y之间的某一事实。

特征函数f(x,y)关于经验分布
P
^
(
X
,
Y
)
\hat{P}(X,Y)
P^(X,Y)的期望:
E
P
^
(
f
)
=
∑
x
,
y
P
^
(
x
,
y
)
f
(
x
,
y
)
=
∑
x
,
y
P
^
(
x
)
P
^
(
y
∣
x
)
f
(
x
,
y
)
E_{\hat{P}}(f)=\sum_{x,y}\hat{P}(x,y)f(x,y)=\sum_{x,y}\hat{P}(x)\hat{P}(y|x)f(x,y)
EP^(f)=∑x,yP^(x,y)f(x,y)=∑x,yP^(x)P^(y∣x)f(x,y)(公式1)
特征函数f(x,y)关于模型P(Y|X)与经验分布
P
^
(
X
)
\hat{P}(X)
P^(X)的期望
E
P
(
f
)
=
∑
x
,
y
P
^
(
x
)
P
(
y
∣
x
)
f
(
x
,
y
)
E_{P}(f)=\sum_{x,y}\hat{P}(x)P(y|x)f(x,y)
EP(f)=∑x,yP^(x)P(y∣x)f(x,y)(公式2)
假设:特征函数f(x,y)关于经验分布 P ^ ( X , Y ) \hat{P}(X,Y) P^(X,Y)的期望应该等于关于模型P(Y|X)与经验分布 P ^ ( X ) \hat{P}(X) P^(X)的期望。那么 P ( y ∣ x ) = P ^ ( y ∣ x ) P(y|x)=\hat{P}(y|x) P(y∣x)=P^(y∣x)(对比公式1和公式2),也就是说数据集的条件概率分布可以反映出模型的条件概率分布。这就可以达到我们的目的了。
最⼤熵模型:假设满⾜所有约束条件的模型集合为
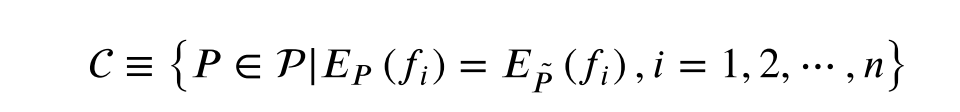
定义在条件概率分布P(Y|X)上的条件熵为:
H
(
P
)
=
−
∑
x
,
y
P
^
(
x
)
P
(
y
∣
x
)
l
o
g
P
(
y
∣
x
)
H(P)=-\sum_{x,y}\hat{P}(x)P(y|x)logP(y|x)
H(P)=−∑x,yP^(x)P(y∣x)logP(y∣x)
4.1.2 最大熵模型学习
优化函数: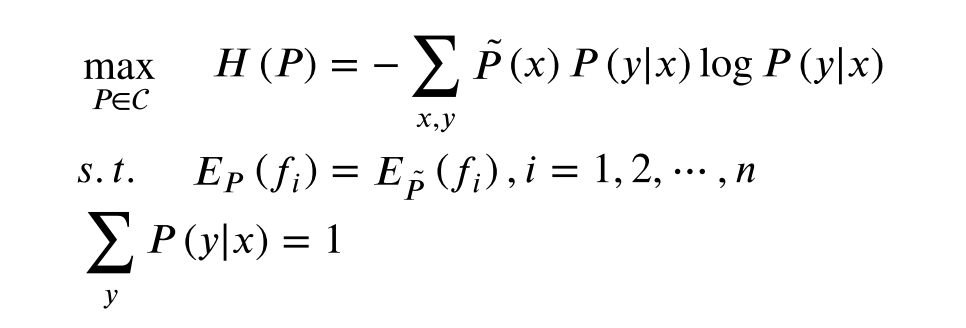
拉格朗日乘子法
1 构建拉格朗日乘子

2 求min
3 求max
最⼤熵模型的极⼤似然估计等价于对偶函数极⼤化。
对偶函数如下:
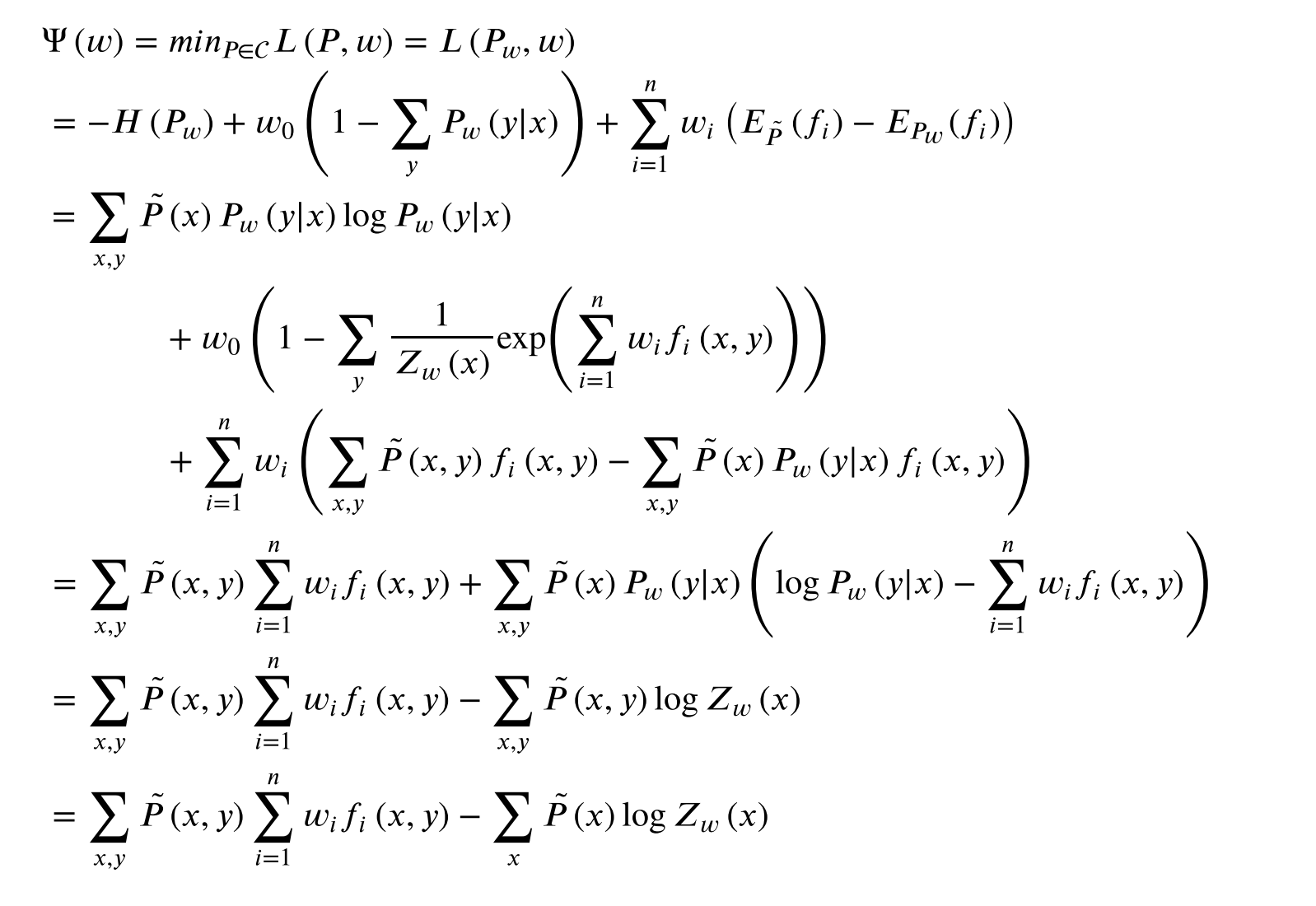
4 模型学习:迭代尺度法
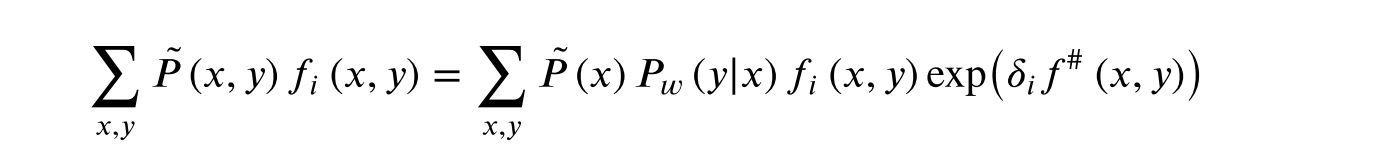
这部分的学习跳过了。直接用结论。
4.2 条件随机场的学习算法
由训练数集,计算经验概率分布
P
^
(
X
,
Y
)
\hat{P}(X,Y)
P^(X,Y)。
目标函数是对数似然函数。计算其中的参数W
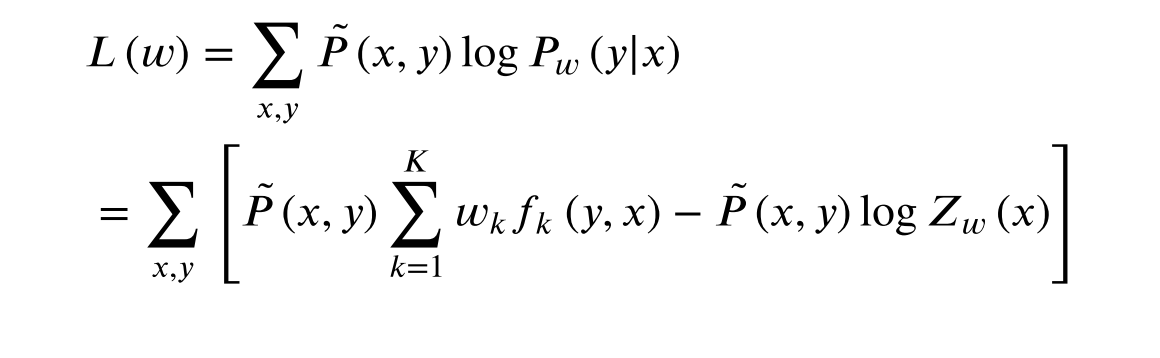
5 条件随机场的预测算法
给定条件随机场P(Y|X)和输入观测序列x,求条件概率最大的标记序列y*。
维特比算法。
公式太多,没有记录。






















 1876
1876











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








