单调栈

参考博客：
https://blog.csdn.net/hebtu666/article/details/82717317
单调栈性质：

1、若是单调递增栈，则从栈顶到栈底的元素是严格递增的。若是单调递减栈，则从栈顶到栈底的元素是严格递减的。

2、越靠近栈顶的元素越后进栈。（显而易见）

用法一
给出一个柱形统计图(histogram), 它的每个项目的宽度是1， 高度和具体问题有关。 现在编程求出在这个柱形图中的最大面积的长方形。

7 2 1 4 5 1 3 3

7表示柱形图有7个数据，分别是 2 1 4 5 1 3 3， 对应的柱形图如下，最后求出来的面积最大的图如右图所示。

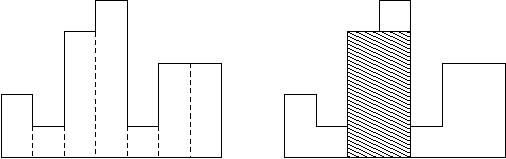
维护一个单调递增栈，所有元素各进栈和出栈一次即可。每个元素出栈的时候更新最大的矩形面积。

当前元素小于栈顶，就可以更新栈顶元素的最大长度了，并且把栈顶弹出，弹出后栈顶还是大，那就继续更新，继续弹出，知道当前元素能放进去。

栈顶下面一个元素一定是它左边第一个比栈顶小的元素，当前元素一定是右边第一个比栈顶小的元素。

用法二 找出矩形数量
假设给你一组数代表矩形的高度，而矩形的宽度为一，问你这样的图形包含多少个矩形。矩形的形状可以相同，但是矩形的位置不能相同

方法----单调栈

• 定义数组 L[ ] :代表左边界 R [ ] :代表右边界 H[ ] : 代表柱体的高度 S [ ] :模拟单调栈 top 栈顶
• 正向扫描 确定柱体的左边界 把零入栈 ，对于高度H【 i】遍历，如果高度比栈顶元素高入栈 否则把大于等于它的元素出栈 它入栈 每次用L【】 记录下标
• 逆向扫描 确定右边界
• 那么矩形数量 (i-L[i])*(R[i]-i)*H[i] 的累加

比较着代码更容易理解

int calc(int *h)
{
    //正向扫描
    s[top=0]=0;
    for(int i=1;i<=n;i++)
    {
        while(top&&h[i]<=h[s[top]]) --top;
        l[i]=s[top];s[++top]=i;
    }

     /*for(int i=1;i<=n;i++)
     {
         cout<<l[i]<<" ";
     }
     cout<<endl;*/
	//逆向扫描
    s[top=0]=n+1;
    for(int i=n;i>=1;i--)
    {
        while(top&&h[i]<h[s[top]]) --top;
        r[i]=s[top];
        s[++top]=i;
    }

   /* for(int i=1;i<=n;i++)
    {
        cout<<r[i]<<" ";
    }
    cout<<endl;*/
	//矩形数量累加
    int res=0;
    for(int i=1;i<=n;i++)
    {
        res=(res+(i-l[i])*(r[i]-i)*h[i]%mod)%mod;
    }
    return res;
}