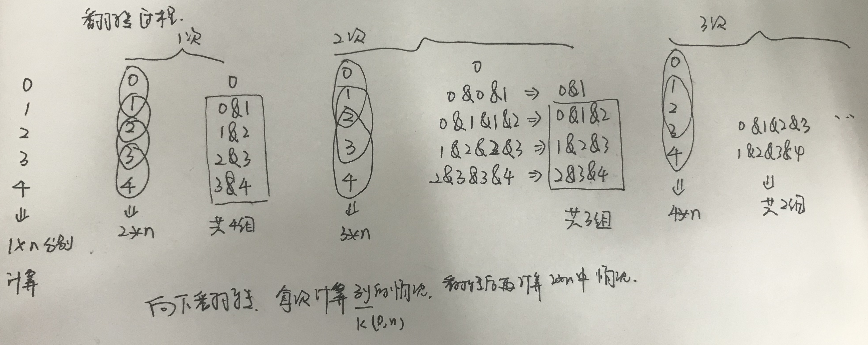
为了笔试,刷了一阵子leetcode,也做了一些DP题目,为了以后更好的理解DP问题,将近期的DP题做了一个思路整理。
相关题目: 前面是目录 后面是题目在leetcode中的链接。
【2】青蛙跳台阶 剑指 Offer 10- II. 青蛙跳台阶问题 | 70. 爬楼梯
【3】把数字翻译成字符串 剑指 Offer 46. 把数字翻译成字符串
【5】打家劫舍 198. 打家劫舍 【213. 打家劫舍 II | 337. 打家劫舍 III】
【7】最长不含重复字符的子字符串 剑指 Offer 48. 最长不含重复字符的子字符串
【10】礼物的最大价值 面试题47. 礼物的最大价值 | 64. 最小路径和
【12】零钱兑换 322. 零钱兑换 | 518. 零钱兑换 II (方案类型)
【13】仅含1的子串数 1513. 仅含 1 的子串数 | 1504. 统计全 1 子矩形 (方案类型)
【15】小w获取的金币
其中1,2,3都是方案类型题目。 4,5属于1维DP。6,7属于也是一维DP。8-9是第i个状态需要考虑前面所有状态的。
8-14对于我来说都是比较难理解的,其中 10相对好做。13 是周赛中字节跳动的算法题。分别对应2/4,3/4位置。14是一道困难题。10-12全是二维度的DP,不仅仅是指 dp is N*N.还指 time is O(N^2)
理论基础[来自链接1]:
动态规划问题的一般形式就是求最值/方案最多个数。
动态规划算法(Dynamic programming,简称DP)通常用于求解以时间划分阶段/具有选择性的动态过程中的某种最优性质的问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策[具有选择性]过程,也可以用动态规划方法方便地求解。 具有选择性指的是在某一状态下,可以根据要求作出不同的选择。
动态规划的穷举有点特别,因为这类问题存在「重叠子问题」,如果暴力穷举的话效率会极其低下,所以需要「备忘录」或者「DP table」来优化穷举过程,避免不必要的计算。
重叠子问题是指,每一个步骤的基本思考方式是一样的。拿青蛙跳台阶来说,那么每一次不是跳一步就是跳两步,那么这个跳几步就是重叠子问题。也就是说,重叠问题的状态选择个数是一定的,不会受其他因素的影响。 面试题45. 把数组排成最小的数 刚开始很容易让人误以为是DP问题,举例如下,很容易的想到,第一个原始 dp[0] = 3. dp[1] = min[dp[0]+'30','30'+dp[0]] 这样的递推公式出来。但是当34 在 30 3 中间插入的时候,不是两种选择,而是3种选择。34 3 30 , 3 34 30,3 30 34三种情况。那么它就不是重叠子问题。因为可选择的状态个数随着插入元素的个数增多了。
[3,30,34,5,9]此外,动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。要符合「最优子结构」,子问题间必须互相独立。也就是说一般都是求解min,max的问题。另外,虽然动态规划的核心思想就是穷举求最值,但是问题可以千变万化,穷举所有可行解其实并不是一件容易的事,只有列出正确的「状态转移方程」才能正确地穷举。
其中我认为状态定义是最难的。只要在认清楚这是一道DP题的基础上,将状态定义清楚,那么就可以顺利的写出状态转移方程了。
在状态定义的时候,要找一个可以表示从小到大[顺序关系-递进关系]关系的状态。定状态的时候,定的是 x状态下,与其对应的上一个状态的关系[上一个状态不一定是X-1,可能是X-2但是X-2的下一个状态会到X这里],即x状态是一个确定的状态,是由上一个状态经过一定的选择出来的状态。一般的状态转移方式如下:
注意:是上一个状态经过选择出来的x的状态,所以对应的x的状态是一个确定状态。不确定的状态是X-1的状态,也就是可供选择的状态。
dp[x] = min/max( dp[x-1],dp[x-1]+a) # 与前一个状态相关,x-1状态下涉及到方案选择问题【1】斐波那契数列
斐波那契数列的数学形式就是递归的,写成代码就是这样:
int fib(int N) {
if (N == 1 || N == 2) return 1;
return fib(N - 1) + fib(N - 2);
}
遇到需要递归的问题,最好都画出递归树,这对你分析算法的复杂度,寻找算法低效的原因都有巨大帮助。
这个递归树怎么理解?就是说想要计算原问题 f(20),我就得先计算出子问题 f(19) 和 f(18),然后要计算 f(19),我就要先算出子问题 f(18) 和 f(17),以此类推。最后遇到 f(1) 或者 f(2) 的时候,结果已知,就能直接返回结果,递归树不再向下生长了。
递归算法的时间复杂度怎么计算?子问题个数乘以解决一个子问题需要的时间。
子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2^n)。
解决一个子问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2) 一个加法操作,时间为 O(1)。
所以,这个算法的时间复杂度为 O(2^n),指数级别,爆炸。
观察递归树,很明显发现了算法低效的原因:存在大量重复计算,比如 f(18) 被计算了两次,而且你可以看到,以 f(18) 为根的这个递归树体量巨大,多算一遍,会耗费巨大的时间。更何况,还不止 f(18) 这一个节点被重复计算,所以这个算法及其低效。
这就是动态规划问题的第一个性质:重叠子问题。如何解决这个问题,将每次计算过的值进行存储。
def helper(n): ##自顶向下
if n< 1 :
return 0
dic = {}
return t(dic,n);
def t(dic,n):
if n == 1 or n==2:
return 1
if n in dic.keys() :
return dic[n]
dic[n] = t(dic,n-1)+t(dic,n-2)
return dic[n]
##自底向上
dic = {1:1,2:1}
def t(n):
if n == 1 or n ==2:
return 1
for i in range(3,n+1):
dic[i] = dic[i-1]+dic[i-2]
return dic[n]上面代码的时间复杂度为O(N),sapce is O(N),由于f(n)至于f(n-1)和f(n-2)相关,那么只用变量pre,cur来存储就足够。空间复杂度变为O(1)。
def t(n): ##只与前两项有关,再次简化
if n == 1 or n ==2:
return 1
pre ,cur = 1,1
for i in range(3,n+1):
sum_ = pre+cur
pre = cur
cur = sum_
return sum_【2】青蛙跳台阶
这个题,和上面的斐波那契数列很相似。
假设一共由N个台阶,那么青蛙一次能跳2个台阶或者1个台阶。当台阶是1时 dp[1] = 1 当台阶是2时dp[2] = 2 (1,1 或者2)
当台阶是3时,dp[3] = dp[1]+dp[2].假设最后一个跳的是2或者1,以此类推往后继续做。
dp[N] = dp[N-1]+dp[N-2]
dp[0] = 1
dp[1] = 1
dp[2] = 2【3】把数字翻译成字符串
分析:a-z:对应的是1-25。数字串12258 可以有两种翻译方法,12翻译成 bc 或者 翻译成 l。类似于前面,青蛙的题目。每一次选择一个台阶【数字】进行跳跃(翻译),或者选择两个台阶【数字】进行跳跃(翻译)。有两种特殊情况只能跳跃一个台阶,(1) 当数字大于25时,只能跳一个台阶(2)当出现‘02’这样的数字时,虽然可以跳一个或者跳两个,但是'02'!=c,只有2=>c 不符合翻译规则。因此递推公式如下:
count = n的位数
if count == 1:return 1
if count==2 and n <=25:return 2
if count ==2 and n>25:return 1
dp[1] = 1
dp[2] = 2/1 # 看题目的具体要求
if [An-2,An-1] > 25:
dp[N] = dp[N-1] # 不能跳2个只能一个个跳
elif [An-2,An-1] == [An-1]:
dp[N] = dp[N-1]
else:
dp[N] = dp[N-1]
class Solution:
def translateNum(self, num: int) -> int:
# 转成 list O(N) O(N)
if num == 0: return 1
l = []
while(num):
l.append(num%10)
num //= 10
print(l)
l = l[::-1]
f = [0 for i in range(len(l)+1)] ##space is O(N)
f[0] = 1
f[1] = 1 ## a,b = 1,1 space is O(1)
for i in range(2,len(l)+1):
if l[i-1]+l[i-2]*10 >25: # 不能跳2个,因为>25,没有符合翻译规则的
f[i] = f[i-1]
elif l[i-1]+l[i-2]*10 == l[i-1]: # 02 不是c 只能一个个翻译 ac,不符合翻译规则
f[i] = f[i-1]
else:
f[i] = f[i-1]+f[i-2]
return f[len(l)]【4】按摩师
分析:今天是否接预约,是受到昨天影响的。子问题间不独立了。为了消除这种影响,在状态数组要设置这个维度不能接受相邻预约,那么就产生了一个可供选择的方案。这个定义是有前缀性质的,即当前的状态值考虑了(或者说综合了)之前的相关的状态值,第 2 维保存了当前最优值的决策,这种通过增加维度,消除后效性的操作在「动态规划」问题里是非常常见的。[参考链接2]
状态方程: 此状态是一个确定的,是由上一个状态做出选择来的。
dp[i][0] = max(dp[i-1][0],dp[i-1][1]) 此状态未接受 ->上一个状态接受了,上一个状态未接受
dp[i][1] = dp[i-1][0]+nums[i] 此状态接受了 ->上一个状态未接受+此状态的
class Solution:
def massage(self, nums: List[int]) -> int:
n = len(nums)
if n ==0 :return 0
if n==1 :return nums[0]
#dp = [ [0 for i in range(2)] for i in range(n+1)]
#dp[0][0] = 0 ## 二维数组
#dp[0][1] = nums[0]
#for i in range(1,n):
#dp[i][0] = max(dp[i-1][0],dp[i-1][1])
#dp[i][1] = dp[i-1][0]+nums[i]
#return max(dp[n-1][0],dp[n-1][1])
### 此状态只与前面状态相关,因此用两个变量节省空间 space is O(1)
a = 0
b = nums[0]
for i in range(1,n):
a,b = max(a,b),a+nums[i]
return max(a,b)
考虑一维度,此状态是一个确定状态,不是接受了就是没有接受。如果接受了,那么上一个状态一定是没有接受的。如果没有接受,那么上一个状态就可以是接受的。
dp[i] = max(dp[i-1],dp[i-2]+nums[i]) #转移方程 是此状态与可以转换到该状态的上一状态并不意味着非要是i-1状态
# 未接受,还是上一个状态的最大值 # 接受了,那么上一个状态是i-2的,和i-1是没有关系的
dp = [0 for i in range(n)]
dp[0] = nums[0] # 第一个天必须接受
dp[1] = max(nums[0],nums[1]) ## 第二天可以接受,也可以不接受,看哪个大
for i in range(2,n):
dp[i] = max(dp[i-1],dp[i-2]+nums[i])
return dp[n-1]
## 再继续空间优化
## a,b = nums[0],max(nums[0],nums[1])
## a,b = b,max(b,a+nums[i])
【5】打家劫舍
打家劫舍
这道题是很经典的一道题。其基本分析思路和上面的按摩师是一样的。因为不能连续偷两家。那么i状态下就有两种可能情况:1,偷了i这家,上一家肯定没有偷,那么累计财富是由i-2状态来的。2,没有偷这家,那么可以是由上一家来的 i-1。故转移方程为:
dp[i] = max(dp[i-1],dp[i-2]+nums[i])
打家劫舍II
这道题相对于I来说,多了一个限制条件,偷了1就不能偷n家的了。因为是一个循环。那么为了破除这个情况。可以考虑在i==1的时候判断是选择偷1还是跳过第一家偷第二家。那么这样可以看成 如果偷了1,那么可以转成再从[3,4,5,..,n-1]。如果没有偷1 是从 [2,3,4,5,...n]的状态中去考虑。
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
if n == 0:return 0
if n ==1 :return nums[0]
if n==2:return max(nums[0],nums[1]) ## 特殊情况
## 选择偷第一家
dp = [0 for i in range(n-1)]
dp[0] = nums[0] # 第一个天必须接受
dp[1] = dp[0]
for i in range(2,n-1):
dp[i] = max(dp[i-1],dp[i-2]+nums[i])
a = dp[n-2] # 最后一个状态
dp = [0 for i in range(n)]
dp[0] = 0 ##第一家选择不偷
dp[1] = nums[1]
for i in range(2,n):
dp[i] = max(dp[i-1],dp[i-2]+nums[i])
b = dp[n-1]
return max(a,b)我自己写的代码:time is O(2N) space is O(2N)
两种状态的不同,无非是一个是[1:n-1],一个是[2:n-2].所以可以简化成如下形式:
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
if n == 0:return 0
if n ==1 :return nums[0]
if n==2:return max(nums[0],nums[1]) ## 特殊情况
def t(nums):
a,b = nums[0],max(nums[0],nums[1])
for i in range(2,len(nums)):
a,b = b,max(b,a+nums[i])
return b
return max(t(nums[1:]),t(nums[:-1]))打家劫舍III
【6】最长连续递增序列
分析:因为要求最长且连续,那么状态i就有两种可能 如果状态 i>i-1的 那么 dp[i] = dp[i-1]+1。如果状态i<i-1的话那么 dp[i] = 1。从新开始从此时刻重新找最大的。每一次将max_值做一次更新。【此方法不是最好的只是可以用DP来做】
class Solution(object):
def findLengthOfLCIS(self, nums):
n = len(nums)
if n <= 1:return n
a = 1
max_ = 1
for i in range(1,n):
if nums[i] > nums[i-1]:
a = a+1
if a>max_:max_=a
else:
a = 1
return max_【7】最长不含重复字符的子字符串
这个题和上一个题基本类似,主要区别点在于如何判断第i个字符是否重复了,那么直接用一条判断语句就行了。
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
n = len(s)
if n<=1:return n
#dp = [1 for i in range(n)]
#
a,max_= 1,1
for i in range(1,n):
if s[i] not in s[i-a:i]:
a= a+1
if a>max_:max_ = a
else:
a = 1
return max_【8】最长上升子序列
与上面的所有的题不相同的点在于此道DP题,不仅要考虑i之前的i-1状态,要考虑的是i之前的所有状态。dp[i]定义为以nums[i]为结尾的最长子序列长度。(不是到nums[i]为止前面的最长的子序列,注意区别)。与上面的区别,在于因为不连续,所以可以从i状态前面的任何一个状态开始,再以这个元素作为结尾。故状态转移方程为:
dp[i] = max(dp[j]) +1 if nums[j] < nums[i] 0<=j<=i-1
dp[i] = max(dp[i],dp[j]+1) if nums[j] < nums[i] 0<=j<=i-1
class Solution: ## O(N^2) O(N)
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
if n<=1:return n
dp = [1 for i in range(n)]
for i in range(1,n): ##
for j in range(0,i): # 0,i-1
if nums[j] < nums[i]:
dp[i] = max(dp[i],dp[j]+1)
return max(dp)由于题目要求需要将复杂度降低为O(NlogN),所以思考如何降低复杂度。由于x状态的确定需要看x状态前面所有的状态,才有了第二层循环,那么重新定义状态是否可以解决问题?是可以的我没做出来,下面分析来自参考链接3.
由题目可知,nums[i]之前的所有状态中最长的序列的最后一个数字越小,那么该序列的总长度边长的可能性越大。
[10,9,2,8,3,7,101,18]以此举例,当 nums[5]时,如果记录了 前面最长的且最后一个元素最小的序列为 [2,3]时,那么碰到7的时候,就可以直接条件元素序列最大长度为[2,3,7]。就不用再去从index=0-4中去找最大的了。
以这样的想法定义了 tail. 表示 到num[i] 为止前面所包含的最长且最后一位数字最小的状态。
因为序列最长为N。所以 tail's size is 1*N. 每到一个节点,去更新tail对应位置的数字,最后返回tail存储的最后一位有效数字,就是最长序列长度。
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
if n <=1 :return n
tail = [0] * n ## 最大长度也就是 n了
tail[0] = nums[0] ## 记录长度为1的时候,初始值
end = 0 ## 记录 tail 最长位置
for i in range(1,n): ## 从i=1开始,寻找最长最后一位数字最小
if nums[i] > tail[end]:
## i位置值大于tail最后一位,长度增加 直接向后继续做 [2,3] -> [2,3,7]
end +=1 # 最长位置更新
tail[end] = nums[i] # 最长位置最后一位更新
else: ## 不大于
left = 0
right = end
while(left<right): ## 注意 left 和 right 的 范围
## 二分法查找较小的nums插入点
mid = left + (right-left)//2
if tail[mid] < nums[i]:
left = mid + 1
else:
right = mid
tail[left] = nums[i] ## 找见合适位置进行插入
end += 1 ## 因为end=0时候记录的是长度为1,所以最后加了1
#print(tail)
return end 由于每次寻找tail的过程相当于是一个排序问题,所以不用判断nums[i]和 nums[i-1]的关系直接按照插入排序来做就行。从而简化代码量。
n = len(nums)
if n <= 1:return n
tails, end = [0] * n, 0
tails[0] = nums[0]
for i in range(1,n):
left,right = 0,end + 1 ## 保证 nums[i] > tail[end]时,可以将nums[i]插入到end+1位置
while (left< right):
mid = left + (right-left)//2
if tails[mid] < nums[i]:
left = mid + 1
else:
right = mid
tails[left] = nums[i]
## 判断 nums[i] > tail[end],如果使得长度增加,那么end也要增加
if left == end+1:
end+=1 ##
end += 1 ##长度下标点 应该从1开始
return end 【9】最长递增子序列个数
第8个求解的是最长子序列长度,由8可以知道递增子序列的个数不唯一,那么再8的基础上可以增加一个count数组来存储以num[i]为结尾的子序列长度,最后挑选出最大长度所对应的求和就可以了。
[1,3,5,4,7,8]以上面为例,count[i]代表以num[i]为结尾的子序列长度个数。
index = 2 [5] 时, dp[i] = 3 ,count[i] = 1 ,表示以5为结束的最长序列长度为3,有1个。
index = 3 [4] 时, dp[i] = 3, count[i] = 1,表示以4为结束的最长序列长度为3,有一个。
index = 4 [7]时,dp[i] = 4,count[i] = count[2]+count[3],表示以7为结束的最长子序列长度为4,有2个。
如果 7前面的最长序列长度+1 大于 dp[i]那么说明 加7 之后序列长度增加,那么count[4]= count[2] 先对应index=2时,
又因为dp[3]+1 = dp[4] 那么 index[3]下面的 最长序列个数也因该增加到7中。所以count[4] += count[3]。
由此可知,当第一次碰见,最长序列的时候 dp[i]+1>dp[i]时候,count[i] = count[j]
当第二次碰见的时候,dp[i]+1 == dp[i] (dp[i]已经是最大),count[i] += count[j] 不同nums结尾的元素都要考虑进去。
因为统计的是每个nums下对应的dp和count,问的时最大的dp,那么就应该先找到最大的dp,然后让相应坐标下的返回。
class Solution: ## O(N^2) O(2N)
def findNumberOfLIS(self, nums: List[int]) -> int:
n = len(nums)
if n <= 1:return n
dp = [1 for i in range(n)] ## 保存当前nums[i]下最长子序列长度,最小为1
count = [1 for i in range(n)] ## 保存当前nums[i]下最长子序列长度的个数
for i in range(1,n):
for j in range(0,i):
if nums[i] > nums[j]: ## dp[i] = max(dp[i],dp[j]+1)
if dp[j] +1 > dp[i]: ##第一次碰到长度可以增加
count[i] = count[j] ## 与之前最大长度对应的个数相同
dp[i] = dp[j] +1
elif dp[j] +1 == dp[i]:
count[i] += count[j]
## 在 nums[j] 上的个数要累加到 nums[i]上,因为对应的nums[i]是不同的
max_= max(dp)
ans = 0
for i in range(0,n):
if dp[i] == max_: ## 以所有nums[i]为结尾的最大长度所拥有的个数
ans += count[i]
return ans 这个题还有一种O(NlogN)和树状数组的方法。我要吐了,不想再看了,先把链接放在这里。
【10】礼物的最大价值
这道题很容易让人产生下面这段代码的思想:从[0,0] 出发 看一下 下和右哪个大,继续沿着较大的走,直到走到最后一个节点[m,n]。
class Solution:
def maxValue(self, grid: List[List[int]]) -> int:
m,n = len(grid),len(grid[0])
i,j= 0,0 ##### 贪心策略 只看一步大小 哪个大 往哪里走 最终不是最优结果
ans = grid[0][0]
while not (i ==m-1 and j==n-1):
if j+1 < n and i+1 < m:
if grid[i][j+1] > grid[i+1][j]:
ans += grid[i][j+1]
j +=1
else:
ans += grid[i+1][j]
i += 1
elif j+1<n and i+1>m:
ans += grid[i][j+1]
j += 1
elif i+1<m and j+1>n :
ans += grid[i+1][j]
i +=1
return ans这样想其实符合一个贪心策略的想法。哪里大,就往哪里走。但是这样走下去,可能不是最优的情况。
比如 [[1,2,5],[3,2,1]] 例子汇总,首先选择向下走,那么就错了。
所以呢,用DP来解决贪心存在的这个问题。
DP之所以能够解决这个问题,是因为DP不是向后看的,而是向前看的。DP的递推公式一般为:
dp[i] = max(dp[i-1],dp[i-1]+ nums[i] )
这样和前一个状态相关的,那么说明X状态是由其上一个状态决定结合此状态决定的的,而不是向下看的。正是因为DP每一步都考虑前面的情况,那么DP才会产生一个最优的情况。
所以,我觉得这也是DP和贪心最大的不同点。贪心:不管前面,只看眼前。 DP:思考前面,结合眼前。
那么针对这个题来说,到达每个点都有两种方式:从下到此处,从右到此处。那么每个点都是到达此点的最大值,到最后一个点依旧也是最大值。所以递推公式如下:
dp[i][j] = max( dp[i-1][j] , dp[i][j-1] ) + grid[i][j] (i-1>=0,j-1>=0)
m,n = len(grid),len(grid[0]) ##O(N^2) O(N^2)
dp = [[0 for i in range(n)] for j in range(m)]
dp[0][0] = grid[0][0]
for i in range(1,m):
dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1,n):
dp[0][j] = dp[0][j-1] + grid[0][j]
for i in range(1,m):
for j in range(1,n):
dp[i][j] = max(dp[i-1][j],dp[i][j-1])+ grid[i][j]
return dp[m-1][n-1]
########## 原地操作 ########
m,n = len(grid),len(grid[0]) ## O(N^2) O(1)
#print(grid)
for i in range(0,m):
for j in range(0,n):
if i-1>=0 and j-1>=0:
grid[i][j] = max(grid[i-1][j],grid[i][j-1])+ grid[i][j]
elif i-1<0 and j-1>=0:
grid[i][j] = grid[i][j] + grid[i][j-1]
elif i-1 >= 0 and j-1< 0:
grid[i][j] = grid[i-1][j] + grid[i][j]
return grid[m-1][n-1]最小路径和:同上一个最大一个最小而已。贪心不能解决。
【11】 n个骰子的点数
分析:骰子个数不同,其基础概率也不同。当n=1时,每种概率都是 1/6. 当n=2时,可以的骰子点数为 (n-6*n). 那么每个点数的基本概率是 (1/6)^2. 那么可以转换成,n=2时,两个骰子可构成(n-6*n)之和的方案个数。是一道求解方案个数类型的题目。且1 和 2 ,2 和1 是两种不同的方案个数->排列数问题。
设 dp[i][j] 表示 共有i个骰子 和为j 的方案个数。共有i个骰子的总数和,可以表示成 i-1个骰子的总数和+ 最后一个骰子点数。因此递推公式也就计算出来了。
dp[i][j] += dp[i-1][j-c] c=1,2,..,6 且 j-c >= i-1 and j-c<<= 6*(i-1)
c为第i个骰子的点数。最后一个骰子只能是1-6.那么前i-1个骰子的总数就是:j-c。但是并非i个骰子的范围可以是 1-6,得保-证前i-1个骰子可以拼凑出。所以添加附加条件。
class Solution:
def twoSum(self, n: int) -> List[float]:
e = 1/pow(6,n) ## 找底
dp = [ [0 for i in range(0,6*n+1)] for i in range(0,n+1)]
## n 个骰子 (n-6*n)种情况
for i in range(1,7):
dp[1][i] = 1
for i in range(2,n+1): ## 第x个骰子 ## O(N^2) O(N^2)
for j in range(i,i*6+1):## 可以构成的骰子种数
if j == i:
dp[i][j] = 1 ## 第一个
continue
for k in range(1,7): # 第i个骰子 只能是 1-6
if j-k >= i-1 and j-k<= 6*(i-1):
## j-k<=6*(i-1)可以省略,因为上一轮中dp[2][23]这种是0 可以直接相加
dp[i][j] += dp[i-1][j-k]
#print(dp)
ans = []
for i in range(n,6*n+1):
ans.append(dp[n][i]*e)
return ans优化空间复杂度:由于递推公式可知,i,j阶段只与 i-1阶段的相关。并且 j 肯定与 j-1,j-2,j-3...,j-6相关。所以,可以将二维度缩减为一维度。但是要从后向前计算。(因为如果不从后向前某些i,j阶段值,会覆盖i-1阶段值)
e = 1/pow(6,n) ## 找底
dp = [0] * 70 ## n<= 11
for i in range(1,7): dp[i] = 1
for i in range(2,n+1):## 前x个骰子总数和,控制更新次数
for j in range(6*i,i-1,-1): ## 从后向前推导
dp[j] = 0 ### 清空上一轮的情况, 此轮结果一定是在j前面不影响计算
for k in range(1,7):##最后一个筛子
if j-k>= i-1 and j-k<= 6*(i-1):
dp[j] += dp[j-k] ## j-k 是i-1个骰子的
return [i*e for i in dp[n:n*6+1]]【12】零钱兑换
第二次做这道题,还是没有做出来。可以用暴力+剪枝的方法做,这里强调DP方法。这道题和其他上面DP不同的是前一个状态不是确定的。比如第10题,只有两条选择不是向下就是向右一直到最后一个节点。但是这道题,以硬币能凑出来的面额为的最小硬币数为状态。存在一个不满足条件或者用最小的硬币数凑不出来想要的硬币数。
状态定义为 当前钱数需要的最小硬币数。
dp[S] = min(dp[S-c]) +1 c = c0, c1,c2...cn 等不同金额的硬币数,并且 S-c>=0
定义初始状态 S= 0 ,dp[0] = 0 ,当 s-c小于0时,自动舍掉这种方案。
假如硬币数为[2,5] amount = 18,那么可以考虑从amount从1开始一直到 18.每个amount下需要的硬币最小数量,然后到最后一个节点。但是有一个问题就是,amount 即使设置了连续1,2,3,4 但是 第一次只有 2,5这个状态,不可能出现1这个状态。如何解决这个问题?
也就是 dp[1] = min(dp[1-2],dp[1-5]) +1 的dp[-1] dp[-4]不可能存在。解决这个问题:x总比coin值大。自动跳过不可能的节点。
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1) ## 0是一种特殊情况,求最小存最大
dp[0] = 0 ## 设置特殊0
for coin in coins: ## 每种coin的情况
for x in range(coin, amount + 1):
## 保证x-coin存在 从而跳过某些状态,保证能够进行
dp[x] = min(dp[x], dp[x - coin] + 1)
if dp[amount] != float('inf') ## 如果等于 float('inf') 就 说明不能拼出amount
return dp[amount]
else:
return -1 零钱兑换 II
这道题是属于方案类型题目。首先想一想小青蛙是如何做的,小青蛙在N台阶前,能跳2步或者1步到N。那么这个题N时,能通过[1,2,5]三种不同的跳台阶的方法到达N。故:
dp[N] = dp[N-5]+dp[N-2]+dp[N-1] 其中 N-5>=0 N-2>=0 N-1>=0
考虑此题的特殊情况: (1)dp[0] = 1
(2)台阶数 和 规定的步幅不符。 当 dp[3] != dp[3-5] + dp[3-2] + dp[3-1] 因为3-5小于0了。
(3)跳2 1 和 跳 1 2 在青蛙看来是不同的,但是在这个题是相同的。即 5 = 2+2+1 和 2+1+2 是一种方案。
如果将1 2 和 2 1看成是不同方案则代码如下:也就是说计算的是排列数。而不是组合数。
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [0] * (amount+1)
dp[0] = 1
max_= max(coins)
for x in range(1,amount+1):
for coin in coins: ## 每一次可以选择一个方案来做
if x-coin>=0: ## 排除不能的方案
dp[x] += dp[x-coin]
return dp[amount]如果1 2 和 2 1 看成相同的方案:那么就是组合问题。dp[i][j] 表示 使用前 i 种硬币能够产生的金额 j 。
dp[i][j] = dp[i-1][j] + dp[i][j-coin[i]] 使用 i-1 种硬币就能凑成 j 种金额+ 使用 i 种硬币 只能够凑成的 j-i 金额。
这道题中,有一位@Liucx的题解,他提到“不知道怎么写状态方程可以画个表格一个一个填,容易找到规律 ”详见链接。 画出表格之后,按照行列进行分析。可以推导出上面的递推。
再次简化 dp[i][j-coins[i]] 实际上是由dp[i-1][j]得来的,也就是 使用 i-1 种时当前为 j-k,那么就可以利用 加了一种硬币到了i种就是 i,j了。
所以递推公式为: 不关心硬币使用的顺序,而是硬币有没有被用到.
dp[i] = dp[i] + dp[i-coin]
class Solution(object):
def change(self, amount, coins):
dp = [0]*(amount+1)
dp[0] = 1
for cost in coins:
for j in range(cost,amount+1):
dp[j] = dp[j] + dp[j-cost]
return dp[amount]
【13】仅含1的子串数
分析:因为求解子串个数, 属于方案类型题目。dp[i]表示到此位置时,一共由多少个子串。
s = "0110111"| s | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 数量 | 0 | 1 | 3 | 3 | 4 | 6 | 9 |
从表格中可以发现,当s[i] == '0'时,出现间断,dp[i] = dp[i-1]
当s[i] == '1' 时, 可以自己罗列下 全1 时候的子串个数:
| s | 1 | 1 | 1 | 1 | 1 | 1 |
| 数量 | 1 | 1+2=3 | 1+2+3=6 | 1+2+3+4=10 | 1+2+3+4+5=15 | 1+2+3+4+5+6=21 |
还可以发现 其实就是一个 d=1的等差数列求和。
可以发现,数量是和在前面有多少个连续的 ‘1’相关的,如果前面是 有 两个‘1’. 那么 子串'1' +1 子串'111'+1,子串'11' +1.所以可发现 s[i]=='1' 时, dp[i] = dp[i-1] + count[i] count表示前面有多少个连续的1.
如果按照上述转义矩阵,Space is O(2N).那么可以简化成 count[i] 存储 index=i 位置前有多少个 连续1.
class Solution:
def numSub(self, s: str) -> int:
n = len(s)
if n == 0:return 0
count = [0 for i in range(0,n)]
ans = 0
for i in range(0,n):
if s[i] == '0':
count[i] = 0
else:
count[i] = count[i-1] +1
ans = (ans % 1000000007 + count[i] % 1000000007) % 1000000007
#print(dp)
return ans做完DP发现这道题,其实没有必要用DP来解决。因为他就是统计一下前面有多少个n。
i,ans = 0,0 ### space is O(1)
while(i<n):
while(i <n and s[i]=='0'): i+=1 ## ans没有变化
j = i
while(j < n and s[j] =='1'): ##### 依旧DP思路
j += 1
ans = (ans % 1000000007 + (j-i)% 1000000007) % 1000000007
i = j
############# 下面是 等差数据求和思路 ####### 参考了此题评论中@Persuing思路
while(i<n and s[j] == '1'): j += 1
ans = ans + ((j - i + 1)*(j - i) / 2) % 1000000007
i = j
return ans 统计全1子矩阵
解法1分析:
这个题如果看每一行的子矩阵的个数是和【13】仅含1的子串数相同的。在这个题的基础上,多加了一个矩阵的问题。如何在行的基础上,增加在行上面的矩阵的信息是关键点。链接 @Keshawn_lu 给出了的思路。
dp[i][j] 表示以 第 i行第j列,连续1个数。 mat = [[0,0,1],[0,1,1]] dp= [[0,0,1],[0,1,2]] 。
如果以 i,j为矩阵右下角的点,向上计算以i,j为右下角的矩阵个数。
dp[1][2] = 2 . 第2行所构成的矩阵个数为2.
dp[0][2] = 1 < dp[0][2] .因此以 第一行 和 第二行 一起构成的矩阵个数 为 1. 所以以 1,2为右下角构成的矩阵为 3.
因此,递推公式为: 分成两个步骤:以行(第一步算每行情况)为基准,去寻找下一种转移状态(行累加 1*n 2*n ....)。
dp[i][j] = dp[i][j-1] +1 if mat[i][j] == 1 ## 计算连续1的个数
for i in range(0,m):
min_ = min(dp[i][j],min_) ## 向上找可以构成的矩阵个数
sum_ += min_ ## 1*n 2*n 3*n 4*n 可构成的矩阵个数之和
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m,n = len(mat),len(mat[0])
ans = 0
dp = [ [0]*n for _ in range(0,m)]
for i in range(0,m):
for j in range(0,n):
if j == 0 and mat[i][j] == 1 :
dp[i][j] = 1
elif mat[i][j] == 1:
dp[i][j] = dp[i][j-1]+1
## 每个 i,j都可以作为 右下角 因为每个i j都要遍历到
mmin = float('inf') ## 最大
for k in range(i,-1,-1): ## 以 [i,..,0][j] 向上翻转
mmin = min(mmin,dp[k][j]) ##
ans += mmin
if mmin == 0:break ## 因为存在0 那么说明再大的 i*n 矩阵也并不会存在了
#print(dp)
return ans解法2:
每行按照上面统计全1字串的方式统计,然后统计 2*n 行的时候,可以按照下面按位与压缩的思想来做。思路来自链接。
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m,n = len(mat),len(mat[0])
ans = 0
for i in range(0,m):
for j in range(i,m): ## 统计每一次翻转时,每一个 1*n,2*n,3*n 中 全一矩阵的个数
now = 0 ## 每一行 前j列中连续1的个数
for k in range(0,m): ### 类似于'011101' 统计1的字串个数
if mat[j][k] == 0: now=0 ## 中断,连续1的个数 为 0
else:
now = now + 1 ## (j,k) 为1 统计个数
ans += now ## 每列每个位置都要 统计进去
j = m-1
while(j>i): ## 计算完 1*n的 做一次全部翻转操作,计算2*n的
for k in range(0,n):
mat[j][k] = mat[j][k] & mat[j-1][k] ## 向下翻转
j -= 1
return ans
### 进行一次翻转后, 只有 1,2,m-1行是翻转后的了
### 进行两次翻转后, 只有 2,3..,m-1是翻转后的了
压缩过程:
【14】 鸡蛋掉落
拿到这个题,我画了这样的树结构,因为出现了上一个状态和下一个状态是相关的, 而且状态到下一个状态都必须是最佳才能保证全局最佳。所以这个题,就是一个DP的问题。DP的问题,在于写状态方程。

这个题就是从0-N的中间位置开始,分成两个部分 [0,(N+1)//2) ,[(N+1)//2,N]。
如果下一个状态分成两种情况:鸡蛋碎和未碎。
如果碎了,那么下一个状态就是,K-1,[0,(N+1)//2//2) [(N+1)//2//2),(N+1)//2)]
如果未碎,那么下一个状态就是,K,[(N+1)//2,(3N+1)//2) [(3N+1)//2,N]
每一次迭代,步数都加1。
停止条件 : K>0 而且 范围内只剩一个数,K>0 而且范围内只剩两个数 。
所以我写了下面这样的代码:把每一个的分解步数都存在L中,然后想让他最后返回最大的。
class Solution:
def superEggDrop(self, K: int, N: int) -> int:
if K == 0 and N==0: return 0
L = []
def test(step,K,l): #鸡蛋个数,list
n = len(l)//2
if K > 0 and len(l)== 1 :
K-=1
return 1
if K > 0 and len(l) == 2:
K-=1
return 2
if K>0:
test(step+1,K-1,[i for i in range(0,n)]) #左
test(step+1,K,[i for i in range(n,N+1)]) #右
if K==0:
L.append(step)
step = 1
test(step,K,[i for i in range(N,-1,-1)])
return max(L)这样写,测试用例能通过,但是里面会出现超过递归深度的问题。
然后我就看了答案,【暴力解】中,其实可以不用列表,把他划分成两个部分就行了,(0-X-1) (X-N)。并且,状态方程,应该是和前一刻状态中的两个对应的(鸡蛋碎和未碎)。那么这个状态转移方程,也应该是两个中的一个输出。所以,不能分成两个test()来做。
(K,[0-N]) = max(dp(K-1,X-1),dp(K,N-X)) 该楼层为X,如果碎了,那么应该是从X-1开始向下找,如果未碎那么就应该是从X时刻开始向上找。 并且 此刻状态,应该是上一个时刻中需要使用的最大次数。【因为如果是最小的话,那么不能够确定F的具体值】假定刚开始的第一个楼层是1,那么确定最后楼层需要的步骤是 max(dp(K-1,X-1),dp(K,X))......假定刚开始的楼层是5(N>5),那么确定最后楼层需要的步骤就是 max(dp(K-1,4),dp(K,5)) 从4开始向下找->1234。未碎,从5开始向上找。
由于开始楼层不固定,所以循环1-N个起始楼层。这个里面最小的那个就应该是 刚开始应该确定的起始楼层。保证需要最小的步骤。【因为不知道起始楼层应该如何确定,所以用暴力解法,每个起始楼层都要循环一遍】暴力法也体现在这里。
临界条件:当楼层是0的时候,不用找,因为不需要步骤就能确定F=0。
当楼层是1的时候,不用找,如果碎了就是F=0 如果未碎就是F=1,故返回 N=1.
当鸡蛋只有一个的时候,不用找,因为肯定到了一个交叉点,在此时返回N。
class Solution:
def superEggDrop(self, K: int, N: int) -> int:
def df(K,N):
if N==0 or N==1 or K==1: return N
min_ = N
for i in range(1,N+1):
t = max(df(K-1,i-1),df(K,N-i))
min_ = min(min_,1+t)
return min_
return df(K,N)暴力解答会超出时间限制。因此采用DP中的每一个状态来存储,以降低时间消耗。
【15】小w获取的金币
此题为字节跳动算法题(4/4)的位置。
题目大概是说:小w到了一个岛上,岛上每一个格子都有一定金币量(可以是正可以是负数)。负数那么就要从总量里面丢掉,正数是他可以拿的。只能从一个格子到其右上、右、右下的位置。可以从最左边的任意一个位置进入。他还带有魔法,可以使一个格子的金币量变成其相反数(只能使用一次)。问他在岛上能够获得的最大的金币是多少?
限制条件: m,n的范围规定。没记住...
有两条说明:(1)首先要想到他不使用魔法的全部过程中,某一个位置能够获取的金币的最大数量,可以用如下计算:
dp[i,j,0] = max( dp[i-1,j-1,0], dp[i,j-1,0], dp [i+1,j-1,0] ) + l[i][j]
(2)他在某个位置是否使用魔法,是与前一个状态未使用魔法相关的。那么就应该在(1)的基础上来做。
dp[i,j,1] = max( max( dp[i-1,j-1,0], dp[i,j-1,0], dp [i+1,j-1,0] ) - l[i][j], max( dp[i-1,j-1,1], dp[i,j-1,1], dp [i+1,j-1,1] ) + l[i][j])
此地方使用魔法是靠前面所有不使用 和 前面已经使用过两个过程来的。在这个过程中,只需要保存最大值,最后返回即可。
至此,题目结束。
首先说明:没有做出来只通过了给出的样例(时间不够了,笔试完才写完的)
分析:(1)如果不给魔法这个条件,那么就是 【10】礼物的最大价值。(2)我认为主要难点在于 如果利用三维数组来做。[因为没有通过所有的测试样例,可能利用三维数组会出现空间复杂度过大的问题]。 (3)如果不给所有的递推公式,是否还能做出来??? 为什么使用三维?状态有多种选择 :(1)走的方向有三个 (2) 是否使用魔法 。其实可供选择的状态越多,那么dp的维度应该是越高的。如果没有说明是否能够想清楚两步走。
在不用魔法的前提下,是很好做的。刚开始想的是,不用三维。直接用 二维 dp + flag 来做。flag 表示第二个递推公式中是否使用魔法这个条件。但是有一个问题,就是在i,j位置使用了,更改了这个i,j位置的值,之后在i,j位置之后的所有值,都是不能使用魔法的。和递推公式也不相符合,所以 二维dp不能用。还是得用三维情况。
下面代码的确返回了 样例中的17。但是其他没有结果。o(╥﹏╥)o 可能是错的。只是记录,如果错了,不吝赐教。
####### 给的样例输入########### O(2(N^2)) O(N^3)
n,m = 4,3 ## n行m列
l = [[1,-4,10],[3,-2,-1,],[2,-1,0],[0,5,-2]] ###岛屿每个位置金币
###################################
dp = [[ [0,0] for i in range(0,m)] for i in range(0,n)]## 初始建立的数组 创建三维情况
#### [0,0] 代表 不使用魔法位置 和 使用魔法位置
for i in range(0,n): ## 初始化
dp[i][0][0] = l[i][0] ## 从最左侧进入
for k in range(0,2):
for i in range(0,n):
for j in range(1,m):
if i-1>=0 and j-1>=0 and i+1 < n: ## 三条都满足
dp[i][j][k] = max(dp[i-1][j-1][k] ,dp[i+1][j-1][k] ,dp[i][j-1][k] )+l[i][j]
elif i-1<=-1 and i+1<n:
dp[i][j][k] = max(dp[i][j-1][k] ,dp[i+1][j-1][k] )+l[i][j]
elif i-1 >=0 and i+1>=n:
dp[i][j][k] = max(dp[i][j-1][k] ,dp[i-1][j-1][k] )+l[i][j]
max_ = -float('inf')
for i in range(0,n): ############是否使用魔法的初始情况############
dp[i][0][1] = -l[i][0]
max_ = max(max(max_,dp[i][0][0]),dp[i][0][1])
for i in range(0,n):
for j in range(1,m): ## 1 的位置更新
if i-1>=0 and j-1>=0 and i+1 < n: ## 三条都满足
dp[i][j][1] = max(max(dp[i-1][j-1][0],dp[i+1][j-1][0],dp[i][j-1][0])-l[i][j],\
max(dp[i-1][j-1][1],dp[i+1][j-1][1],dp[i][j-1][1])+l[i][j])
elif i-1<=-1 and i+1<n:
dp[i][j][1] = max(max(dp[i][j-1][0],dp[i+1][j-1][0])-l[i][j],\
max(dp[i][j-1][1],dp[i+1][j-1][1])+l[i][j])
elif i-1 >=0 and i+1>=n: #dp[i][j-1],dp[i-1][j-1]
dp[i][j][1] = max(max(dp[i][j-1][0],dp[i-1][j-1][0])-l[i][j],\
max(dp[i][j-1][1],dp[i-1][j-1][1])+l[i][j])
max_ = max(max(max_,dp[i][j][0]),dp[i][j][1])
print(max_)【16】392. 判断子序列 的后续挑战
这道题本身没有什么难度, 利用双指针来判断s[i] 和 t[j]就可以了,如果s[i]==t[j] i++ j++ 否则 j++.直到最后判断是否i==len(s)。这样做时间复杂度为O(m+n) m= len(s) n=len(t) K个s,平均时间为 O(K*(m+n))
在后续挑战中,给出了s子串数量巨大的时候,应该如何求解的问题? 存储跳转的index->DP
因为t没有变化,主要的时间是浪费在了从头开始找与s[i]相匹配的每一个t[j]上面,那么可以根据t来建立一个帮助快速定位的矩阵,这样每次移动的时间复杂度为O(1)。可将每次查找降低为O(n*26+m),如果有K个s,那么平均时间为O(n*26+K*m)
n*26是初始建立依据t的索引表所用的时间,K*m是查询s所用的时间。空间复杂度为O(n*26) 26 因为全是小写字母。
利用dp[i][j] 来表示i位置之后包含i位置,第一次出现字符j的index。(这样就可以直接跳到index位置)
dp[i][j] = i t[i] = j 如果t[i]位置的元素刚好是j,那么j第一次出现的位置就是i
dp[i][j] = dp[i+1][j] t[i] != j 如果t[i]位置出现的元素不是j,那么就要看下一个位置出现第一次出现j的index。这样能保证 字符j出现的位置是第一次。
一般情况下: dp[i] 是根据上一个状态而来的,也就是dp[i-1] dp[i-2]....。但是上面的递推公式是与后面的dp[i+1][j]相关的。因此要从后向前来写递推公式。这也是这个题不同之处。这也给我们解决DP问题提供了一个思路(如果根据题目,当前状态不是和上一个状态相关,而是根据后面状态反映,那么可以考虑倒写DP过程)
n,m= len(s),len(t)
dp = [ [0]*26 for i in range(m)] ## 每一个位置每一个字符的跳转情况
dp.append( [m]*26) ## dp初始化,为了让最后一个位置的字符有所指向,dp[i+1]不溢出
## 也是为了 跳转过程中的 break
for i in range(m-1,-1,-1):
for j in range(0,26): ## 26个元素
if ord(t[i])-ord('a') == j: ## t[i]位置的字符 正好是j,t[i]位置第一次出现j的index为i
dp[i][j] = i
else:
dp[i][j] = dp[i+1][j] ## dp[i+1]
########## s的每次找操作##################
i,k = 0,0
while(i<n):
k = dp[k][ord(s[i])-ord('a')] ## 在t[k]位置第一次出现s[i]的index
if k == m and i<=n-1: ## 跳转失败,直接到最后一个不存在的,
## 正常情况下最多就是 k=m-1 and i=n-1,k怎么也不会到m
return False
i += 1
k += 1 ##该轮匹配,下一轮从下一个点开始
return True 【16】吃掉N个橘子 的最少天数
更新于20200817,类似于钱币兑换,想利用DP来做,代码如下。
class Solution:
def minDays(self, n: int) -> int:
if n<=1: return n
if n<=4: return 2
dp = [0 for i in range(0,n+1)]
dp[1] = 1
dp[2] = 2
dp[3] = 2
for i in range(4,n+1):
if i%2 == 0 and i%3==0:
dp[i] = min(min(dp[i-1]+1,dp[i-i//2]+1),dp[i-2*(i//3)]+1)
elif i%2 != 0 and i%3 !=0:
dp[i] = dp[i-1]+1
elif i%2 == 0 and i%3 != 0:
dp[i] = min(dp[i-1],dp[i-i//2])+1
elif i%2 != 0 and i%3 == 0:
dp[i] = min(dp[i-1]+1,dp[i-2*(i//3)]+1)
#print(dp)
return dp[n] 由于n可以等于 2*10^9 ,所以超出时间限制了。主要可能是因为开辟不了这么大的内存空间,此外O(N)最大是 2*10^9 ,可能也存在过大的难题。
因此这个题,利用DFS+记忆化存储来做。将递归的每一次结果保存,有点类似于斐波那契数列,中为了降低递归深度而将值进行存储。题解来自:链接 @illusion
class Solution:
def minDays(self, n: int) -> int:
dic = {}
def dfs(i):
if i ==0 or i ==1 :return i
if i in dic.keys() : return dic[i]
a = min(1+i%2+dfs(i//2),1+i%3+dfs(i//3))
dic[i] = a
return dic[i]
return dfs(n)解释:假设n=5,这时候应该是mp[5]=1+mp[4]. 按照上面的思想,mp[5] = min(1 + 1 + mp[2], 1 + 2 + mp[1],5). 前面的其实是将减一的情况和除二的情况结合,后面的是和减一之后除三的情况结合.所以还是三种情况。























 522
522











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










