比RSA更好MI多变元公钥加密系统（附例题）

最新推荐文章于 2023-09-18 16:39:44 发布

唠嗑！

最新推荐文章于 2023-09-18 16:39:44 发布

阅读量531

点赞数 2

分类专栏：经典密码文章标签：网络安全线性代数抽象代数

本文链接：https://blog.csdn.net/forest_LL/article/details/124087265

版权

经典密码专栏收录该内容

12 篇文章 2 订阅

订阅专栏

本文章将用一个“toy"例子来理解Matsumoto-Imai密码系统（MI）。

一. 定义与铺垫

k为含有 $q=2^2=4$ 个元素的有限域，表达形式如下：

$k=GF(2^2)$

域中非零元素的乘法群可以由域元素 $\alpha$ 产生， $\alpha$ 满足如下等式：

$\alpha^2+\alpha+1=0$

域k中的元素可以由 $\lbrace0,1,\alpha,\alpha^2\rbrace$ 表示，且它们的加法与乘法定义的运算如下表：

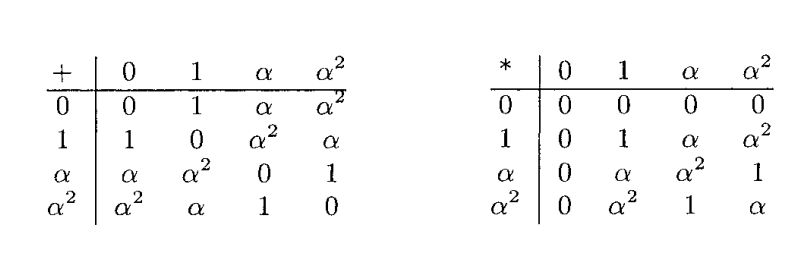
取 $n=3$ ，且g(x)为k[x]中一个不可约多项式，所以取定 $g(x)=x^3+x+1$ ，K的定义如下：

$K=\frac{k[x]}{x^3+x+1}$

在这个例子中 $\theta$ 的取值有两种可能性，也就是 $\theta=1$ 或者 $\theta=2$ ，在后续的讨论中 $\theta$ 取2。映射 $\tilde F$ 的定义如下：

$\tilde F=X^{1+4^2}$

映射 $\tilde F$ 的求逆过程定义如下：

$\tilde F^{-1}(X)=X^{26}$

$L_1$ 和 $L_2$ 给定如下：

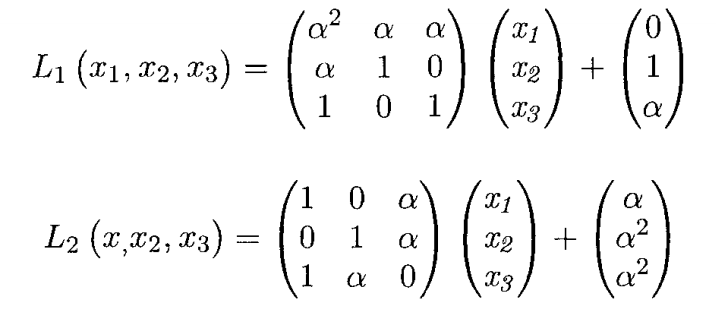
二. 获得公钥多项式

明文变量表示为 $x_1,x_2,x_3$ ，为了获得公钥多项式，首先需要计算 $\phi^{-1}\circ L_2(x_1,x_2,x_3)$ ，如下形式：

$\phi^{-1}L_2(x_1,x_2,x_3)=(\alpha+x_1+\alpha x_3)+(\alpha^2+x_2+\alpha x_3)x+(\alpha^2+x_1+\alpha x_2)x^2$

将上式子用X表示，接着计算 $\tilde F(X)$ ，如下：

$\tilde F(X)=X^{1+4^2}=X\cdot X^{16}$

依次对X进行乘方运算，此过程不算太难。由于是在特征为2的有限域k内进行运算的，所以不会有超过二次的项，最终计算 $\tilde F(X)$ 的结果如下：

$1+\alpha^2x_1+\alpha x_2+x_3+x_1x_2+\alpha x_1x_3+\alpha^2x_2x_3+(\alpha+\alpha x_1+x_2+\alpha^2 x_3+x_1^2+\alpha^2 x_1x_2+x_2^2+x_2x_3)x+(\alpha^2+\alpha^2x_1+\alpha x_2+\alpha x_3+x_1^2+x_1x_2+\alpha x_1x_3+\alpha^2x_2^2+\alpha x_2x_3+\alpha^2x_3^2)x^2$

最后一步计算 $L_1\circ\phi(X)$ 就可以得到公钥多项式，如下：

$\bar f_1(x_1,x_2,x_3)=1+x_3+\alpha x_1x_3+\alpha^2x_2^2+\alpha^2x_2x_3+x_3^2$

$\bar f_2(x_1,x_2,x_3)=1+\alpha^2x_1+\alpha x_2+x_3+x_1^2+x_1x_2+\alpha^2x_1x_3+x_2^2$

$\bar f_3(x_1,x_2,x_3)=\alpha^2x_3+x_1^2+\alpha^2x_2^2+x_2x_3+\alpha^2x_3^2$

三. 加密过程

取明文 $(x_1',x_2',x_3')=(1,\alpha,\alpha^2)$ ,加密过程为分别计算 $y_1',y_2',y_3'$ ，如下：

$y_1'=\bar f_1(1,\alpha,\alpha^2)=0$

$y_2'=\bar f_2(1,\alpha,\alpha^2)=0$

$y_3'=\bar f_3(1,\alpha,\alpha^2)=1$

到此，密文则为 $(0,0,1)$

四. 解密过程

解密的过程需要三步的计算 $L_1^{-1},\tilde F^{-1}$ 和 $L_2^{-1}$ 。第一步计算的式子如下：

$L_1^{-1}(y_1,y_2,y_3)=\begin{pmatrix}\alpha^2\;1\;1\\1\;\alpha^2\;\alpha\\ \alpha\;1\;0 \end{}\begin{pmatrix}y_1-0\\y_2-1\\y_3-\alpha\\ \end{}$

将密文(0,0,1)代入，可得如下计算：

$L_1^{-1}(0,0,1)=\begin{pmatrix}\alpha\\ \alpha\\1 \end{}$

得到的结果写为 $X=\alpha+\alpha x+x^2$ ，代入 $\tilde F^{-1}$ 进行计算如下：

$\tilde F^{-1}(X)=X^{26}=\alpha+x^2$

此过程的计算可以利用二进制法（也就是平方相乘法）。在实际的应用中，由于X的指数t是非常大的，所以运算时间会较长。如果将t写成二进制模型 $\theta$ ，此举会大大加快计算 $X^t$ 的过程。

到目前为止已经得到 $(\bar z_1,\bar z_2,\bar z_3)=(\alpha,0,1)$ 。最后一步 $L_2^{-1}$ 的计算法则可见如下：

$L_2^{-1}(y_1,y_2,y_3)=\begin{pmatrix}\alpha^2\;\alpha^2\;\alpha\\ \alpha\;\alpha\;\alpha\\1\;\alpha\;1 \end{}\begin{pmatrix}y_1-\alpha\\y_2-\alpha^2\\y_3-\alpha^2 \end{}$

代入 $(\alpha,0,1)$ 计算如下：

$L_2^{-1}(\alpha,0,1)=(1,\alpha,\alpha^2)^T$

此结果与最初的明文一致。

五. MI密码系统的密钥长度与效率

MI密码系统的公钥是一组次数为2的多项式 $\bar f_1,\ldots,\bar f_n\in k[x_1,\ldots,x_n]$ 。每个多项式的项数计算如下：

$1+n+\frac{n(n+1)}{2}=\frac{(n+1)(n+2)}{2}$

因此，当q>2时，公钥可取自域k的系数个数可计算如下：

$\frac{n(n+1)(n+2)}{2}$

当q=2时，由于满足 $x_i^2=x_i$ ，所以没有平方项，这种情况下的公钥长度会更短一些。

在1988年Matsumoto-Imai原来建议的参数规模， $k=GF(2^8),n=32$ ，公钥比RSA要更大一些。但是MI公钥加密系统在计算效率上，仍然占有很大的优势。如果选择较小的q=|k|，就可以把乘法运算表存入内存，实现基于域k中的非零元素组成循环乘法群。因为RSA需要用到大数运算，使得MI加密比RSA更快。在MI密码系统的解密运算中，计算 $\tilde F^{-1}$ 需要大量运算，此种技术细节也可以应用。

综合以上，MI公钥加密系统是第一个预想比RSA更快实现且具有相同安全性的方案。

唠嗑！

关注

2
点赞
踩
3

收藏

觉得还不错? 一键收藏
打赏
0
评论
比RSA更好MI多变元公钥加密系统（附例题）

本文章将用一个“toy"例子来理解Matsumoto-Imai密码系统（MI）。一. 定义与铺垫k为拥有个元素的有限域，表达形式如下：域中非零元素的乘法群可以由域元素产生，满足如下等式：域k中的元素可以由表示，且它们的加法与乘法定义的运算如下表：取，且g(x)为k[x]中一个不可约多项式，所以取定，K的定义如下：在这个例子中的取值有两种可能性，也就是或者，在后续的讨论中取2。映射的定义如下：映射的求逆过程定义如下：和给定如下：二. 获得公钥..
复制链接

扫一扫