【图论】—— 最小生成树

---

最小生成树

给定一张边带权的无向图 , 。由 V 中全部 n 个顶点和 E 中 n - 1条边构成的 无向连通子图 被称为 G 的一棵生成树。

边的权值之和最小的生成树被称为无向图 的最小生成树

---

定理

任意一颗最小生成树一定包含无向图中权值最小的边

证明：

反证法。假设无向图  存在一棵最小生成树不含权值最小的边。

设   是无向图中边权最小的边。 把 e 添加到树中，e 会和树上从 x 到 y 的路径一起构成一个环，并且环上其他边的权值都比 z 大。因此，用 e 代替环上的其他任意一条边，会形成一棵权值和更小的生成树，与假设矛盾。故假设不成立，原命题成立。

证毕。

推论： 

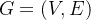
给定一张无向图   。从 E 中选出  条边构成 G 的一个生成森林。若再从剩余的   条边中选  条添加到生成森林中，使其成为 G 的生成树，并且选出的边的权值之和最小，则该生成树一定包含这  条边中连接生成森林的两个不连通节点的权值最小的边。

---

Kruskal算法 

Kruskal算法就是基于上述推论的。Kruskal算法 总是维护无向图的最小生成森林。
 

最初，可以认为生成森林由 0 条边构成，每个节点格子构成一棵仅包含一个点的树。
 

在任意时刻，Kruskal算法从剩余的边中选出一条权值最小的，并且这条边的两个端点属于生成森林中两棵不同的树（不连通），把该边加入输出森林。
 

图中节点的连通情况可以用并查集维护。

算法流程：

1. 建立并查集，每个点各自构成一个集合
2. 把所有边按权值从小到大排序，依次扫描每条边  
3. 若 x, y 属于同一集合（连通），则忽略这条边，继续扫描下一条
4. 否则，合并 x, y 所在的集合，并把 z 累加到答案中
5. 所有边扫描完成后，第 4 步中处理过的边就构成最小生成树

时间复杂度为 

---

代码实现

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, M = 2 * N, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge
{
    int a, b, w;
    
    bool operator< (const Edge &W) const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);
    
    // 初始化并查集
    for(int i = 1; i <= n; i ++ ) p[i] = i;
    
    int res = 0, cnt = 0;
    for(int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        
        a = find(a), b = find(b);
        if(a != b)
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }
    
    if(cnt < n - 1)  return INF;
    return res;
}


int main()
{
    cin >> n >> m;
    
    for(int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }
    
    int t = kruskal();
    
    if(t == INF) puts("impossible");
    else cout << t << endl;
}

---

例题：洛谷 P1396 营救
 

 

这道题本质上就是kruskal算法的一个应用（用最短路求也可）
将所有的边按照权重进行排序后，从小到大按照kurskal算法的顺序进行连通

当 s 和 t 第一次连通的时候，此时求的的便是这两点间的最短距离（贪心的思想：若存在其其他可连通的路径，其边权之和一定大于等于第一次所连通的边权之和）

---

AC代码 

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, M = 2 * N, INF = 0x3f3f3f3f;

int n, m, s, t;
int p[N];

struct Edge
{
    int a, b, w;
    
    bool operator< (const Edge &W) const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);
    
    // 初始化并查集
    for(int i = 1; i <= n; i ++ ) p[i] = i;
    
    int res = 0, cnt = 0;
    for(int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        
        
        
        a = find(a), b = find(b);
        if(a != b)
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
        
        if(find(s) == find(t)) return w;
    }
}


int main()
{
    cin >> n >> m >> s >> t;
    
    for(int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }
    
    int t = kruskal();
    
    cout << t << endl;
    
    return 0;
}