声明:本文为博主原创文章,未经博主允许不得转载。
在直接线性标定方法中,并没有考虑相机镜头的非线性畸变,而在Tsai提出的两步标定法中很好的解决了这个问题。相关理论推导如下:
1、相机畸变模型
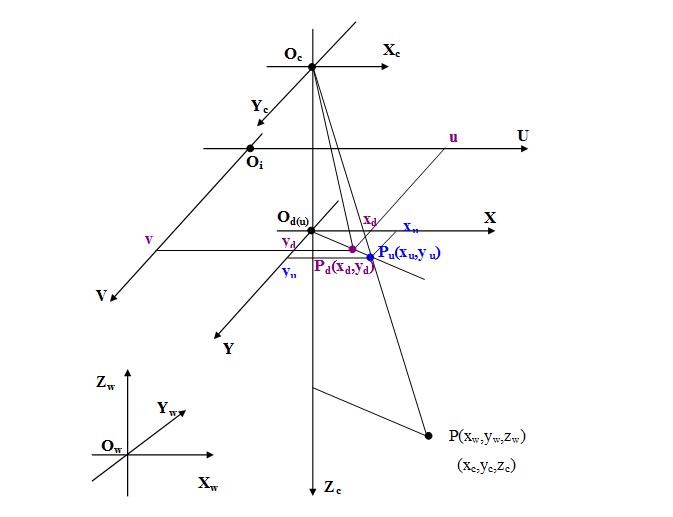
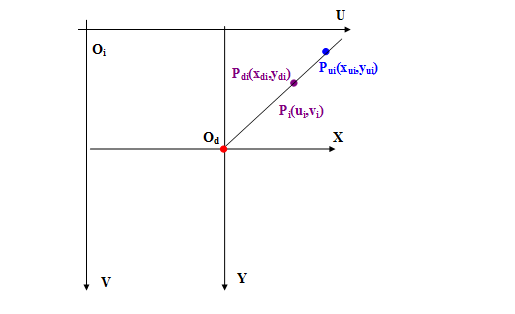
我们可以看出在上图中可以分以下几个坐标系:
① 像机坐标系Oc
② 图像像素坐标系Oi
③ 世界坐标系Ow
④ 实际图像物理坐标系Od
⑤ 理想图像物理坐标系Ou
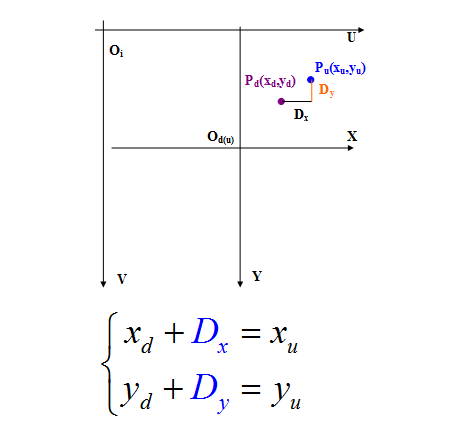
2、畸变量
此时,畸变量可分为在X方向和Y方向上,这种畸变量我们只考虑了径向畸变,其他畸变右以忽略不计,径向畸变本身是有一定的线性关系的,下面畸变模型的讲解时也会说到:
Dx:x方向畸变量
Dy:y方向畸变量
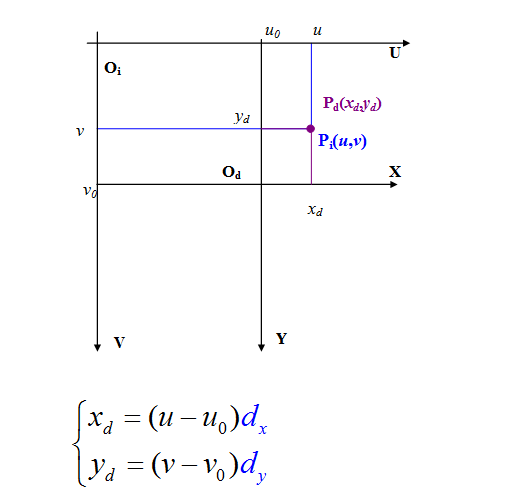
3、实际图物理坐标系与像素坐标系的关系(基本关系)
dx: x方向的像素距(每个像素在x方向的长度)
dy: y方向的像素距(每个像素在y方向的长度)
4、基本公式(在线性标定的基础上)
5、畸变的总体表示
径向畸变Dr
离心畸变Dt
薄棱镜畸变Dp
6、三种畸变的数学模型
径向畸变及其规律(径向约束):
离心畸变:
薄棱镜畸变:
总畸变:
畸变系数:
径向畸变:k1
离心畸变:p1, p2
薄棱径畸变:s1, s2
7、模型参数
内参数:
焦比:fu, fv
图像中心(主点)坐标:u0,v0
畸变系数: k1, p1, p2, s1, s2
外参数:
平移矢量:T
旋转矩阵:R
典型标定方法
利用像机畸变模型建立约束方程
确定优化目标函数
以非线性优化方法求解
缺点:
优化程序计算复杂,速度慢
标定的结果取决于初始值
8、两步标定法正式开始
1987年由Tsai提出
第一步:求除tz外的所有外参数
利用径向排列约束(RAC)
线性求解
第二步:求其余参数
非线性优化
9、两步法的前提
假设:
u0,v0已知
只考虑二阶径向畸变
主点既是图像中心又是径向畸变中心
10、公式推导
得到以下公式:
11、径向约束公式
上面已经求出:
综合可得:
乘开:
12、第一步
1、求中间变量
为了方便表示与计算,用参数将变量代替:
2、 求|ty|
4、求tx
5、求R:
6、确定ty符号:
设ty>0, 求其它参数
用远离图像中心的特征点计算:
假设条件正确:
xci与ui-u0同号
yci与vi-v0同号
剩余参数:fu,fv, tz, k1
约束方程:
13、第二步
剩余参数:fu,fv, tz, k1
已知:
求:
方法:非线性优化
确定初始值:
k1=0, dv=1
忽略非线性畸变,求解fv和tz
14、U0,V0的标定
直接光学方法
变焦距法
径向排列约束法
直接光学法
用一束激光照射像机镜头
在光路上放一张有孔的纸
使激光的入射光线与反射光线重合
用像机摄取包含激光光斑的图象
光斑的中心坐标即为光心坐标
调整困难但精度较高
变焦距法
条件:光心与镜头的缩放中心重合
实现:
不同距离分别对多个特征点成像
每个特征点一个线性方程
径向排列约束法
利用共面标定板,取zwi=0
非线性优化求解
15、小小总结一下:
前面标定方法共性:
已知特征点二维图像坐标与三维空间坐标
需要标定参照物
统称:传统标定方法
优点:适用任意摄像机模型,标定精度高
不足:需标定参照物,某些应用中难以实现








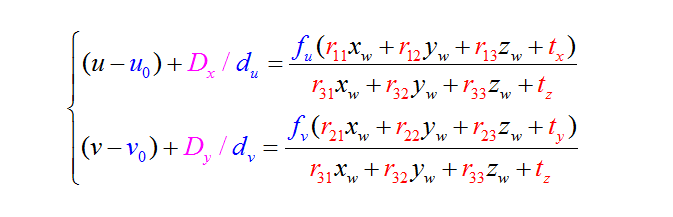
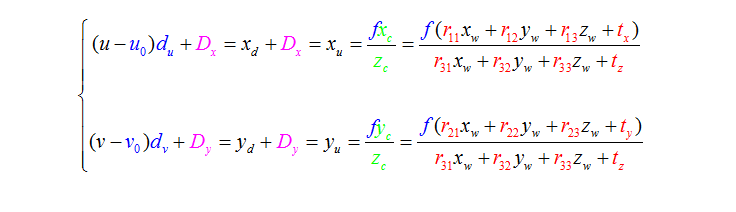
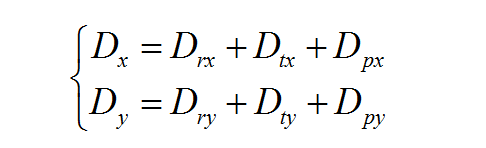
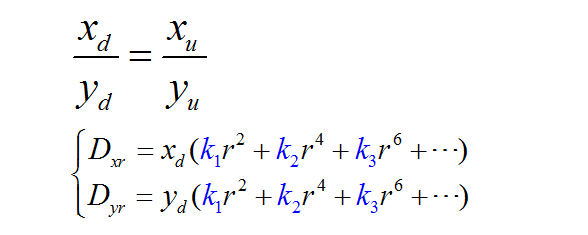
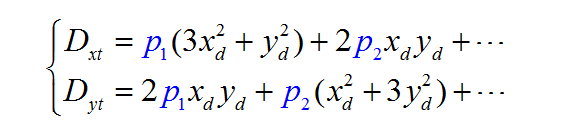
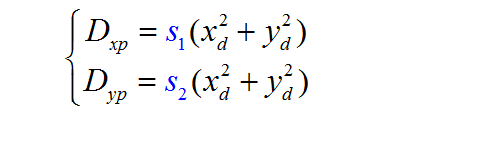
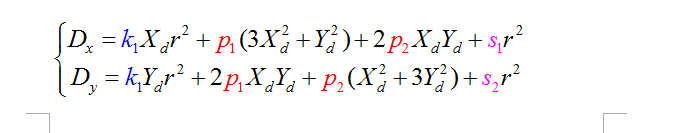
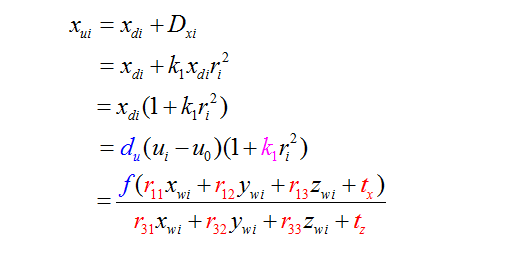
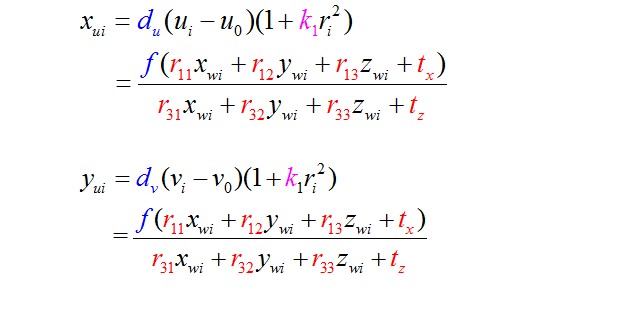
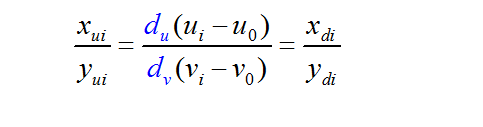
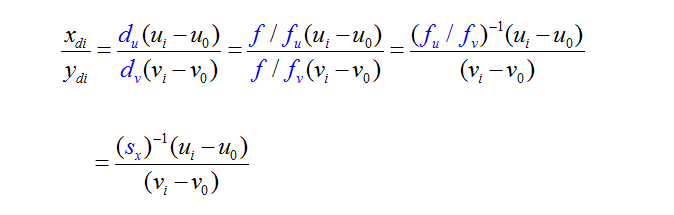
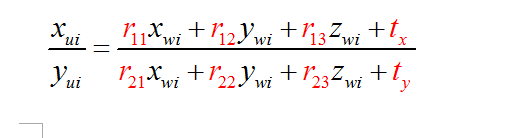
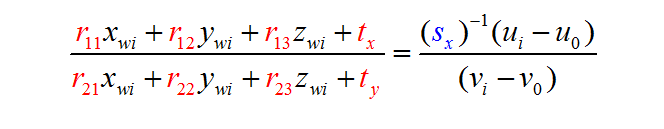
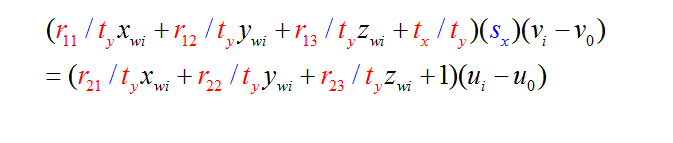
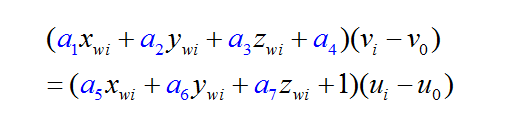
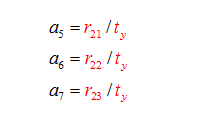
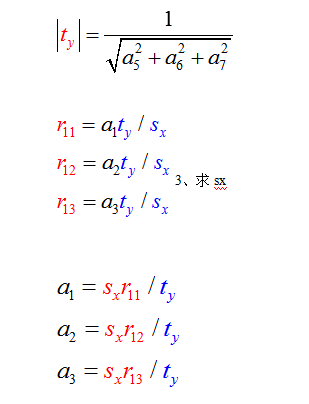
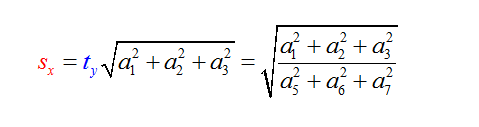
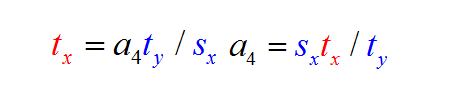
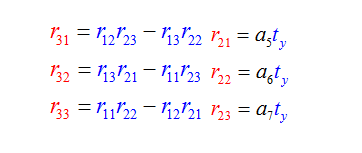
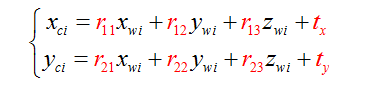
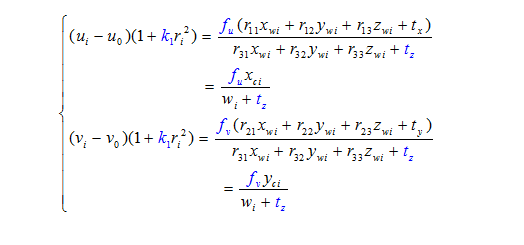
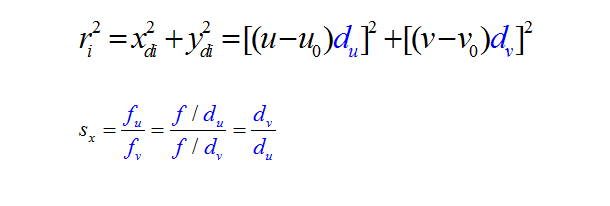
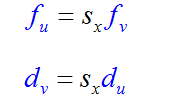
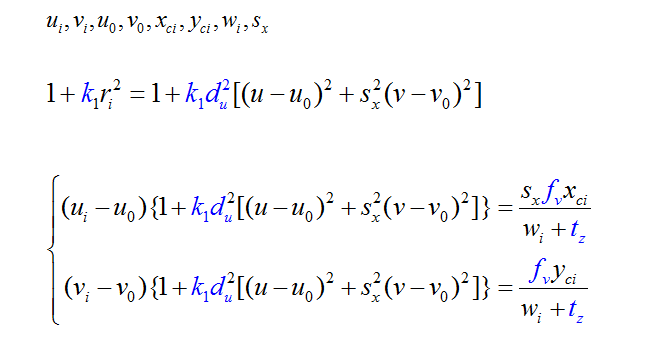
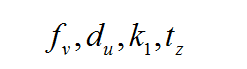
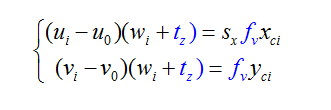
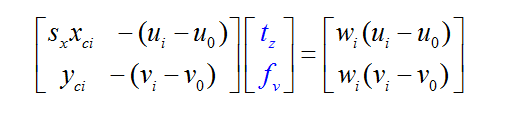
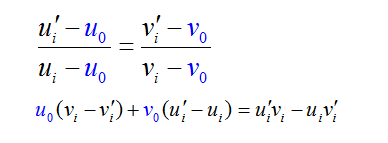
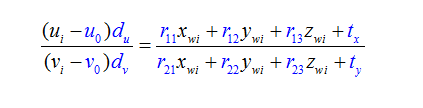
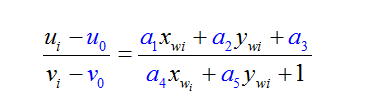
















 2550
2550

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








