494. Target Sum

• Total Accepted: 16739 
• Total Submissions: 38242 
• Difficulty: Medium
• Contributors: kevin.xinzhao@gmail.com

You are given a list of non-negative integers, a1, a2, ..., an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

Example 1:

Input: nums is [1, 1, 1, 1, 1], S is 3. 
Output: 5
Explanation: 

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

There are 5 ways to assign symbols to make the sum of nums be target 3.

Note:

1. The length of the given array is positive and will not exceed 20.
2. The sum of elements in the given array will not exceed 1000.
3. Your output answer is guaranteed to be fitted in a 32-bit integer.

解题思路：

对于一个数组nums，在增加加号或者减号之后他的和值范围是 [-sum(nums),  sum(nums)]。对于nums中的每一个数，都有加和减两种选择。得到的这两个结果再加或者减第二个数，又有4个结果。用dp[i + sum(nums)] 来记录每次操作之后使得和为i的方法数，经过一轮操作后dp[S+sum(nums)] 就是答案。

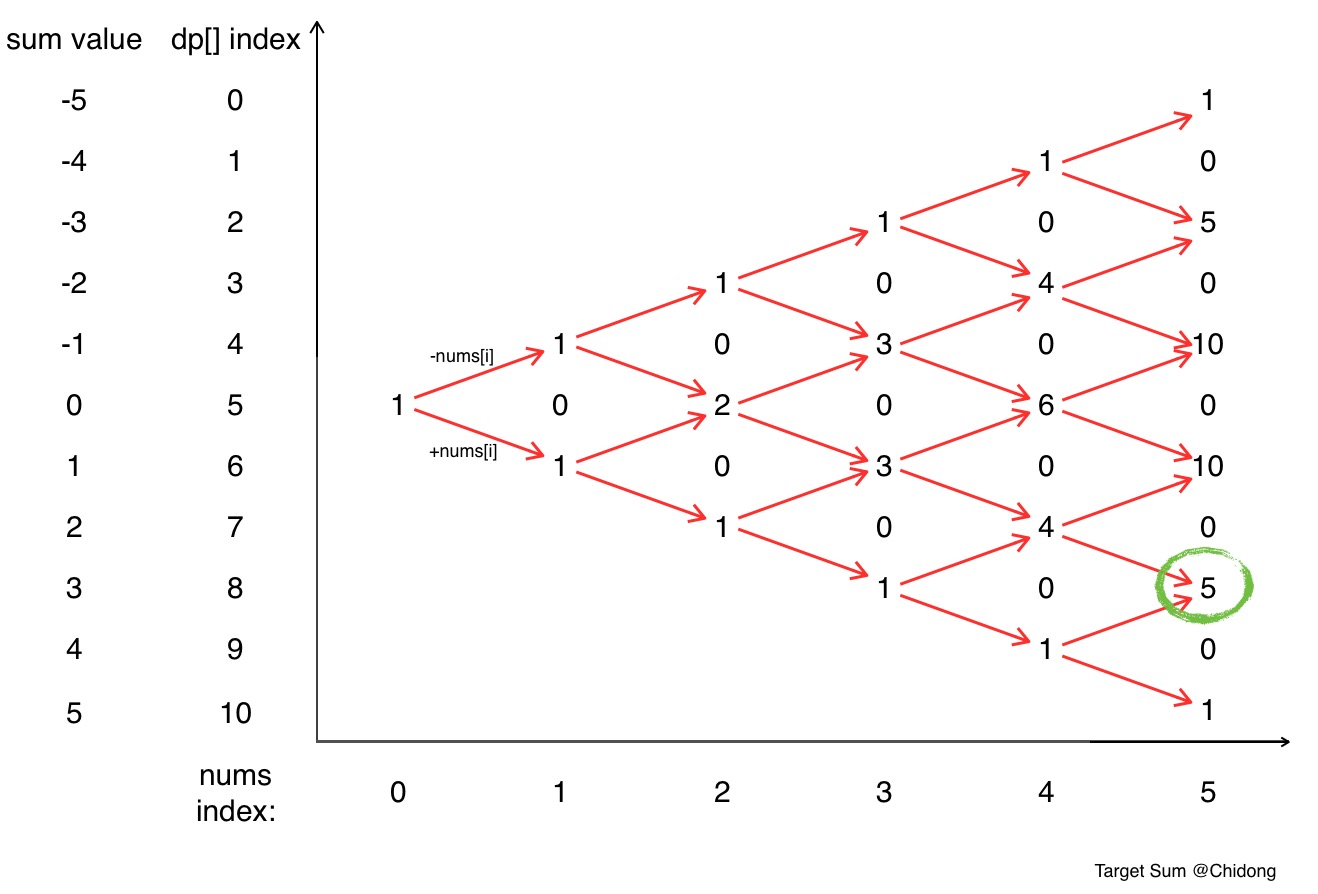
代码：

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int S) {
        int sum = 0;
        for(int i = 0; i < nums.size(); i++)
        	sum += nums[i];
        if(S > sum || S < -sum || (S+sum)%2 != 0)
        	return 0;
        int dp[2001] = {0};
        dp[sum] = 1;
        for(int i = 0; i < nums.size(); i++){
        	int next[2001] = {0};
        	for(int j = 0; j < 2 * sum + 1; j++){
        		if(dp[j] != 0){
        			next[j - nums[i]] += dp[j];
        			next[j + nums[i]] += dp[j];
        		}
        	}
        	for(int j = 0; j < 2 * sum + 1; j++)
        	    dp[j] = next[j];
        }
        return dp[sum + S];
    }
};