1.欧氏距离
数学定义
对于n维空间中的两个点:
-
P = (p₁, p₂, ..., pₙ)
-
Q = (q₁, q₂, ..., qₙ)
它们之间的欧氏距离定义为:
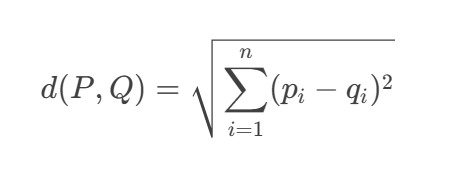
几何解释
在二维空间中,欧氏距离就是两点间的直线距离(勾股定理)
在三维空间中:
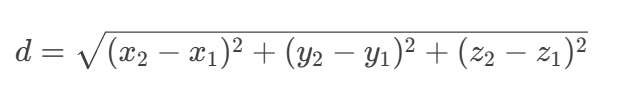
python代码实现:
import numpy as np
def euclidean_distance(point1, point2):
"""
计算两点之间的欧氏距离
参数:
point1, point2 -- 两个点的坐标(列表、元组或数组)
返回:
两点间的欧氏距离
"""
# 将点转换为numpy数组
p1 = np.array(point1)
p2 = np.array(point2)
# 计算坐标差值的平方和,然后开平方
return np.sqrt(np.sum((p1 - p2)**2))
# 示例
pointA = [1, 2, 3]
pointB = [4, 5, 6]
distance = euclidean_distance(pointA, pointB)
print(f"点A({pointA})和点B({pointB})之间的欧氏距离: {distance:.4f}")
# 点A([1, 2, 3])和点B([4, 5, 6])之间的欧氏距离: 5.1962
2.曼哈顿距离
曼哈顿距离(Manhattan Distance),也称为城市街区距离(City Block distance)、L1 距离或出租车几何(Taxicab geometry),是一种在几何空间中度量两点间距离的方法。
核心概念
-
定义: 两个点在标准坐标系(笛卡尔坐标系)上的绝对轴距总和。
-
公式: 对于二维平面上两点 P1(x1,y1)P1(x1,y1) 和 P2(x2,y2)P2(x2,y2),它们的曼哈顿距离 dd 定义为:
-
推广到 n 维: 对于 n 维空间中的两点
和
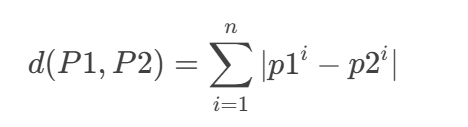
3.切比雪夫距离
切比雪夫距离(Chebyshev distance),也称为棋盘距离(Chessboard distance)或 L∞ 度量(L-infinity metric),是一种在向量空间中定义的度量方式。它得名于俄罗斯数学家帕夫努季·切比雪夫(Pafnuty Chebyshev)。
对于 n 维空间中的两个点:
-
P = (p₁, p₂, ..., pₙ)
-
Q = (q₁, q₂, ..., qₙ)
它们的切比雪夫距离定义为 各坐标数值差绝对值的最大值:
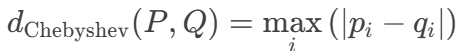
4.闵可夫斯基距离
闵可夫斯基距离是多元空间中的广义距离度量,由德国数学家赫尔曼·闵可夫斯基提出。它统一了多种常见距离度量,通过参数 p 控制距离计算方式。
数学定义
对于 n 维空间中的两点:
-
P = (p₁, p₂, ..., pₙ)
-
Q = (q₁, q₂, ..., qₙ)
闵可夫斯基距离公式为:
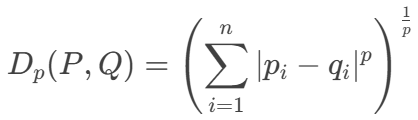
其中 p ≥ 1 是决定距离计算方式的参数。

5.标准欧氏距离
标准欧氏距离是针对传统欧氏距离的改进版本,专门解决量纲差异和特征尺度不一致的问题。它通过对各维度进行标准化处理,使不同特征在距离计算中获得公平的权重。
核心定义
对于 n 维空间中的两个点:
-
X = (x₁, x₂, ..., xₙ)
-
Y = (y₁, y₂, ..., yₙ)
标准欧氏距离公式为:
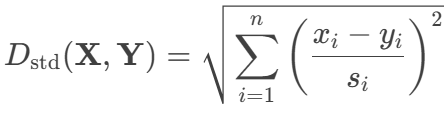
其中:
-
和
是
维空间中的两个数据点
-
和
分别表示两个点在第
个维度上的特征值
-
是第
个维度在整个数据集上的标准差(样本标准差计算为
=
-
是特征维度总数
完整数据集与标准欧氏距离计算示例
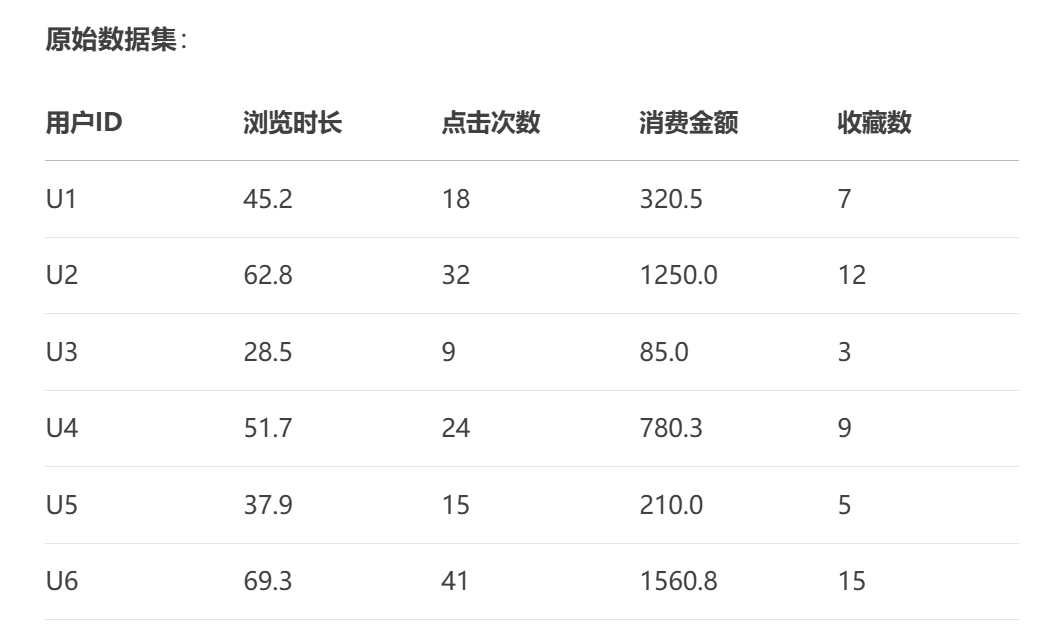
数据集描述
场景:电商用户行为分析
样本数:6位用户
特征维度:
-
浏览时长(分钟/天):连续数值
-
点击次数(次/天):计数数据
-
消费金额(元):货币数据
-
收藏商品数(个):离散数值
计算目标
计算用户 U2 (62.8, 32, 1250.0, 12) 与 U6 (69.3, 41, 1560.8, 15) 的标准欧氏距离
分步计算过程
步骤1:计算各维度的标准差
使用样本标准差公式:
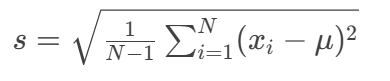
-
浏览时长:
-
数据:[45.2, 62.8, 28.5, 51.7, 37.9, 69.3]
-
均值:
-
方差:
-
标准差:
-
-
点击次数:
-
数据:[18, 32, 9, 24, 15, 41]
-
均值:
-
方差:
-
标准差:
-
-
消费金额:
-
数据:[320.5, 1250.0, 85.0, 780.3, 210.0, 1560.8]
-
均值:
-
方差:
-
标准差:
-
-
收藏数:
-
数据:[7, 12, 3, 9, 5, 15]
-
均值:
-
方差:
-
标准差:
-
标准差汇总:
步骤2:计算标准化差异
对于每个特征维度,计算:标准化差异
-
浏览时长:
-
点击次数:
-
消费金额:
-
收藏数:
步骤3:计算平方和
平方和=∑(标准化差异)^2=
步骤4:计算最终距离
Python 完整实现验证
import numpy as np
from scipy.spatial.distance import seuclidean
# 原始数据集
data = np.array([
[45.2, 18, 320.5, 7], # U1
[62.8, 32, 1250.0, 12], # U2
[28.5, 9, 85.0, 3], # U3
[51.7, 24, 780.3, 9], # U4
[37.9, 15, 210.0, 5], # U5
[69.3, 41, 1560.8, 15] # U6
])
# 计算各列标准差
stds = np.std(data, axis=0, ddof=1)
# 输出: [14.17, 11.04, 574.28, 4.09]
# 提取目标用户
U2 = data[1] # [62.8, 32, 1250.0, 12]
U6 = data[5] # [69.3, 41, 1560.8, 15]
# 方法1:手动计算
diff = (U2 - U6) / stds
squared_sum = np.sum(diff**2)
manual_dist = np.sqrt(squared_sum) # 1.306
# 方法2:Scipy函数
scipy_dist = seuclidean(U2, U6, stds) # 1.306
# 方法3:sklearn标准化后计算欧氏距离
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler().fit(data)
U2_std = scaler.transform([U2])
U6_std = scaler.transform([U6])
sklearn_dist = np.linalg.norm(U2_std - U6_std) # 1.306
6.余弦距离
余弦距离是衡量两个向量方向差异的距离度量,通过计算它们夹角余弦值的补数得到。它在高维稀疏数据(如文本、推荐系统)中表现优异,对向量幅度不敏感。
核心定义
给定两个非零向量 A = (a₁, a₂, ..., aₙ) 和 B = (b₁, b₂, ..., bₙ),余弦距离公式为:
-
分子:向量点积(内积)→ 衡量方向一致性
-
分母:向量模的乘积 → 归一化处理
-
范围:[0, 2]
-
0:完全相同方向
-
1:正交(90°夹角)
-
2:完全相反方向(180°夹角)
-
几何意义
-
只关注向量夹角θ,忽略长度差异
-
距离值 = 1 - cosθ
-
当向量平行时距离最小(θ=0° → cos0°=1 → 距离=0)
完整计算示例:新闻文档相似度
数据集描述
场景:3篇科技新闻的关键词词频统计
特征维度:["AI", "5G", "量子计算", "区块链"]
文档向量:
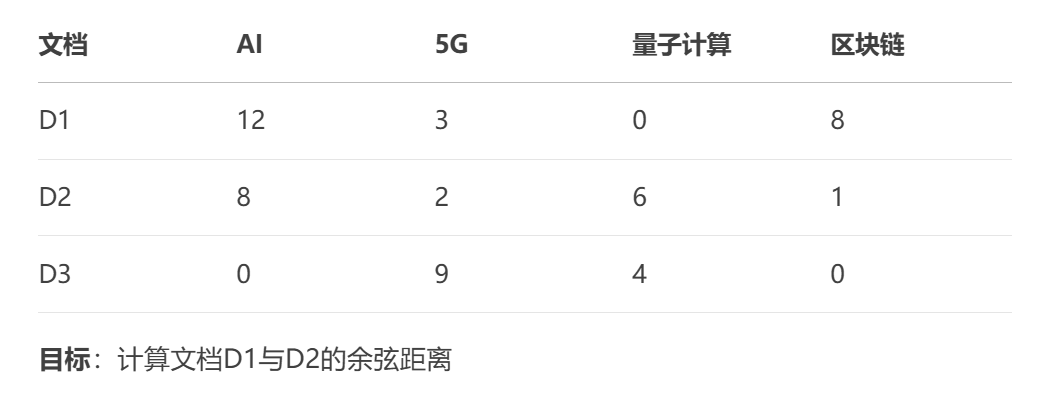
分步计算过程
-
计算点积
-
计算模长
-
计算余弦相似度
-
计算余弦距离
7.了解内容
(1).汉明距离
汉明距离(Hamming Distance)是信息论和计算机科学中衡量两个等长字符串差异程度的度量,定义为两个字符串在相同位置上不同字符的个数。
核心概念
-
定义
-
对于两个长度相同的字符串 s1 和 s2,汉明距离 dH(s1,s2) 是满足 s1[i]≠s2[i]s1[i]=s2[i] 的位置 i 的数量。
-
公式表示:
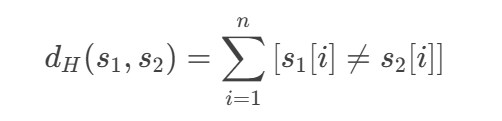
其中 [⋅] 是指示函数(若条件成立则为 1,否则为 0),n 是字符串长度。
-
-
关键限制
仅适用于等长字符串!若长度不同,汉明距离无定义。

(2).杰卡德距离公式
杰卡德距离(Jaccard Distance) 是衡量两个集合差异性的常用指标,与杰卡德相似系数(Jaccard Similarity Coefficient)互补。它广泛应用于数据挖掘、生态学、推荐系统等领域,特别适合处理非数值型数据(如集合、二进制向量、文本特征等)。
核心公式
设两个集合 AA 和 BB:
-
杰卡德相似系数(Jaccard Similarity):
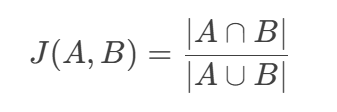
-
杰卡德距离(Jaccard Distance):
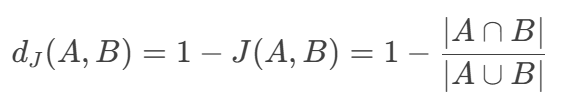
其中:
-
∣A∩B∣:集合 A 和 B 的交集大小(共同元素数量)
-
∣A∪B∣:集合并集大小(所有唯一元素数量)
几何意义
-
取值范围:[0,1]
-
dJ=0 → 两个集合完全相同(A=B)
-
dJ=1 → 两个集合无共同元素(A∩B=∅)
-
-
对称性:dJ(A,B)=dJ(B,A)
-
不满足三角不等式(非度量距离)




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








