【后缀数组系列】一、基本概念

如果你没有听说过后缀数组，那么我敢肯定，你确实没怎么处理过字符串相关的算法问题。

————题记

对于解决字符串相关的问题，后缀数组是一把利器。它经常被用来解决字符串相关的各种复杂问题。下面开始介绍后缀数组。

后缀数组 int SA[N]

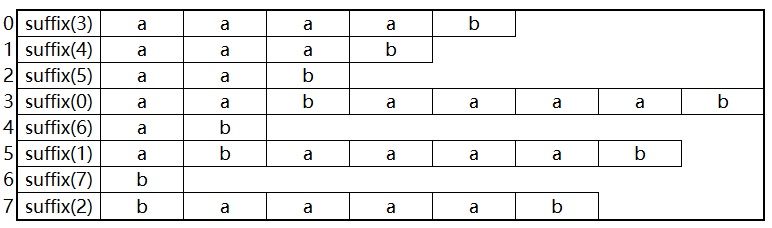
从后缀字符串开始。对于字符串S[9] = "aabaaaab"来说，字符串的长度为8，所以不包括空子串，共有8个后缀字符串，我们分别用suffix(i)来表示，i为0到7。

由上图可以看到，suffix(7)的长度为1，suffix(0)的长度为8。

通常，我们把后缀数组记作int SA[N]，显然，这是一维整型数组。这里，SA[i]中的下标i 表示的是 排名。而SA[i]中存储的是排在第i名的后缀串所对应的下标。
也就是说，假如串suffix(k)在所有的后缀串中排名为i，则有SA[i] = k 。注意，排名也从0开始计数。

我们把这8个后缀串，按照字典序，从小到大进行排序，得到如下结果：

因此，SA[0] = 3，SA[1] = 4，SA[2] = 5，SA[3] = 0，SA[4] = 6，SA[5] = 1，SA[6] = 7，SA[7] = 2

因为每个后缀串对应的下标不一样，所以SA[i]的值也肯定完全不一样。

总结一下，如果存在 SA[i] == k，则我们可知道 suffix(k)串的排名为i。再强调一遍，SA[i]中的下标i表示的是排名为i，SA[i]中存储的值为排名为i的后缀串对应的下标。

这样，通过后缀数组SA[i]，我们就可快速得到 suffix(SA[i]) < suffix(SA[i+1])，其中，0≤i≤N-1，N为原字符串的长度。

简记为 SA[i]中存储的是下标，表示 “排第i名的是谁”。

名次数组 int Rank[N]

名次数组Rank[i]表示的是suffix(i)在所有后缀串中从小到大排序的名次。

由上面的图 可知，suffix(7)按从小到大排名，排在第6位，所以Rank[7] = 6.同理，Rank[0] = 3，Rank[1] = 5，Rank[2] = 7，Rank[3] = 0，Rank[4] = 1，Rank[5] = 2，Rank[6] = 4.

简单地说，就是Rank[i]中存储的是名次，表示suffix(i)排在第几名。

后缀数组与名次数组的关系

名次数组中存储的是名次，后缀数组中存储的是下标。

SA[i]中存储的是下标，表示 “排第i名的是谁”。Rank[i]中存储的是名次，表示“suffix(i)排在第几名”。

由定义可知，后缀数组与名次数组互为逆关系。也就是说，Rank[SA[i]] == i，SA[Rank[i]] == i。

在求出名次数组后，就可以在O(1)时间内比较任意两个后缀串的大小。

在求出后缀数组后，就可以在O(1)时间内知道排名第i的是谁。

只要求出其中的一个，就可以在O(n)时间内推出另外一个。

//已知后缀数组SA，求名次数组Rank
//这里的i相当于第i名
for(int i = 0; i < N; i++)
	Rank[SA[i]] = i;
	
//已知名次数组Rank，求后缀数组SA
//这里的i相当于下标i
for(int i = 0; i < N; i++)
	SA[Rank[i]] = i;

height 数组

这里的i是排名。定义height[i]中存储的是 suffix(SA[i-1]) 和 suffix(SA[i]) 的最长公共前缀的长度，也就是排名相邻的两个后缀的最长公共前缀的长度。

1≤i≤N-1

height[i]表示第i-1名和第i名，这两个后缀串的最长公共前缀的长度。

比如，因为suffix(SA[0]) = "aaaab", suffix(SA[1]) =  "aaab"，所以 height[1] = 3.

h数组

这里的i是下标。h[i]=height[rank[i]]，也就是suffix(i)和在它前一名的后缀串的最长公共前缀。

LCP(i,j)

对排名i,j  定义LCP(i,j)=lcp(suffix(SA[i]),suffix(SA[j])，其中i,j 均为0 至n-1 的整数。LCP(i,j)也就是后缀数组中排名第i 和第j 的后缀串的最长公共前缀的长度。

其中，函数lcp(u,v)=max{i|u==v}，也就是从头开始顺次比较字符串u 和v 的对应字符，对应字符持续相等的最大位置，称为这两个字符串的最长公共前缀。

LCP(i,j)=min{height[k] | i+1≤k≤j}，也就是说，计算LCP(i,j)等同于询问一维数组height 中下标在i+1 到j 范围内的最小值。

对于i≥1 且Rank[i]≥1，一定有h[i]≥h[i-1]-1