卡特兰数相关问题

引例

从一个简单的问题引入:

电影票每张50元，如果有 m+n 个人排队买票，其中m个人各持有50元面值的钞票1张，另外n个人各持有100元面值的钞票1张，而票房没有预备找零．有多少种方法可以将这m+n个人排成一列，顺序购票?

乍一看，这个问题完全就是一个最简单的全排列问题，只要将所有可能排列下来，然后逐个检查就行了。

实际上，这可以说是一类十分经典的问题，我们可以将上述问题抽象为这样一个泛化的问题:

假如有M种操作a，以及N种操作b。现在要求顺序执行这总共M+N种操作，且要求：在整个操作的任何一个阶段时，已经执行过的a操作数量不能大于已经执行过的b操作

上述问题的演变模型有很多，我们举几个例子:

1. 进出栈
   一个栈(无穷大)的进栈序列为1,2,3,…n,有多少个不同的出栈序列?
2. 方格移动
   在一个$m\times n$的网格中，从左下角的原点O(0,0)出发，每次向右或向上移动，要求任意时刻点不得在y = x这条线之上。

3. 括号匹配

   求由n对括号形成的合法括号表达式的个数

以上问题的解均和一个数有关：卡特兰数(Catalan)。

卡特兰数

分析

什么是卡特兰数？在谈卡特兰数前先让我们分析一下之前的问题的求解。首先我们以最简单出栈入栈问题为例:

首先，每一种进出栈的顺序都与出栈序列一一对应．也就是说，如果我们用+1表示进栈，−1表示出栈，那么题中示例中的出栈序列1,3,4,2与进出栈顺序:

+1,+1,−1,+1,+1,−1,−1,−1,

是对应的。

那么对n个数的序列，总的进出栈顺序是给2n个里面挑n个填入+1其余的是-1，共 $C_{2n}^n$ 种吗？

答案是否定的，这是因为出栈的前提是有进栈动作，于是要求每个排列中的前若干项和均不为负数，也就是说诸如排列:

1,−1,−1,1,1,−1,−1,1

这样的是无效的。也就是说真正的答案 = $C_{2n}^n$ - 不合法的排列数量。

所以现在的问题就是：不合法的排列有几种？

不合法的排列数

那么如何计算不合法的排列数量呢？这里我们使用一种折线发。前面讲到过，出入栈和从(0, 0)到(n, n)问题是等价的。

由于没找到合适的图，所以放了一张以y = 0为分界线的图，不过原理都是一样的。

我们不妨来看一种不合法的情况，对应的折线是这样的:

我们可以看到，任何一个不合法的折线一定会经过 $y=x+1$ (对应图中的 $y=-1$ )，我们将第一个与这条线的点之后的部分以 $y=x+1$ (对应图中的 $y=-1$ )为对称轴做一个对称变化，可以发现最后的落点一定会是 $(n-1,n+1)$ (对应图中的 $(2n,-2)$ )。

这说明什么？这说明**在2n步选择中，有n - 1步选了向右，所有的选法加起来就是 $C_{2n}^{n-1}$ **。

因此无效的排列总共有 $C_{2n}^{n-1}$ 种。

卡特兰数

结合上面两节，我们现在可以知道了，一共的排列方法种类数量为:
$$C_n=C_{2n}^n-C_{2n}^{n-1}=\frac{1}{n+1}{C}_{2n}^n$$
这个 $C_n$ 就被称为卡特兰数。

变形的卡特兰数

然而到目前为止，我们还是无法解决一开始提出的那个问题。因为刚才我们一直讨论的卡特兰数有一个要求：两种操作的数量相同，都是n。

那么，当操作不同时该怎么办呢？

其实这个问题很简单，刚才我们不是走了一个正方形的棋盘吗？现在换成矩形就行了:

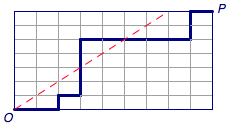
稍加思索我们发现，这个和之前的没有任何区别。假设宽为m，高为n，且有 m > n，那么经过对称处理后终点落在了 $(n-1,m+1)$。

也就是说，最终结果为:
$$C_{m+n}^n-C_{m+n}^{n-1}$$