介电常数、等效介电常数

电容的大小和导体周围介质的特性有关。如果当两个导体周围填充的介质为空气时，

电容为C,把空气换成另外一种介质后两导体间电容变为C,那么这种新的介质的介电

常数为

通常所说的介质的介电常数实际上是一种相对介电常数，习惯上使用下标r表示，这一

参数没有单位，表征的是与空气相比这种介质会使电容量改变多少。所有的介质都使用相

对介电常数来表示这种特性，因此常常省略“相对”一词，简称为“介电常数”。如果一种

介质的介电常数为4,说明相对于空气来说，换上这种介质后会使导体间电容增加到原来的

4倍。介电常数是一个非常有用的概念，和信号完整性中很多重要的参数都有关，比如传输

线的特性阻抗、延时等。

介电常数是物质本身的固有特性，和物质的大小形状无关，但和介质的组成成分有关。

加工PCB常用的板材一般都是玻璃纤维编织结构和树脂混合压制而成的，玻璃纤维和树脂

的介电常数不同，因此，板材所表现出来的介电常数实际上是这两种介质的某种平均后的

结果，板材介电常数的大小与树脂和玻璃纤维含量的比例有关。PCB加工过程中使用的板

材分PP和Core两种，Core是已经固化的两面为铜箔的板材，加工PCB的时候Core中树

脂和玻璃纤维的相对含量可以认为不变，因此介电常数相对稳定。PP(也称半固化片)在

加工PCB过程中树脂会由于高温而融化，在压合过程中可能树脂的含量会有变化，因此，

PCB加工完成后PP的介电常数与加工过程有关。

导体周围填充的是均匀介质的时候，导体感受到的介电常数就是介质的介电常数，如

果周围填充的介质是非均匀介质的时候，那么导体感受到的介电常数和两种介质的特性都

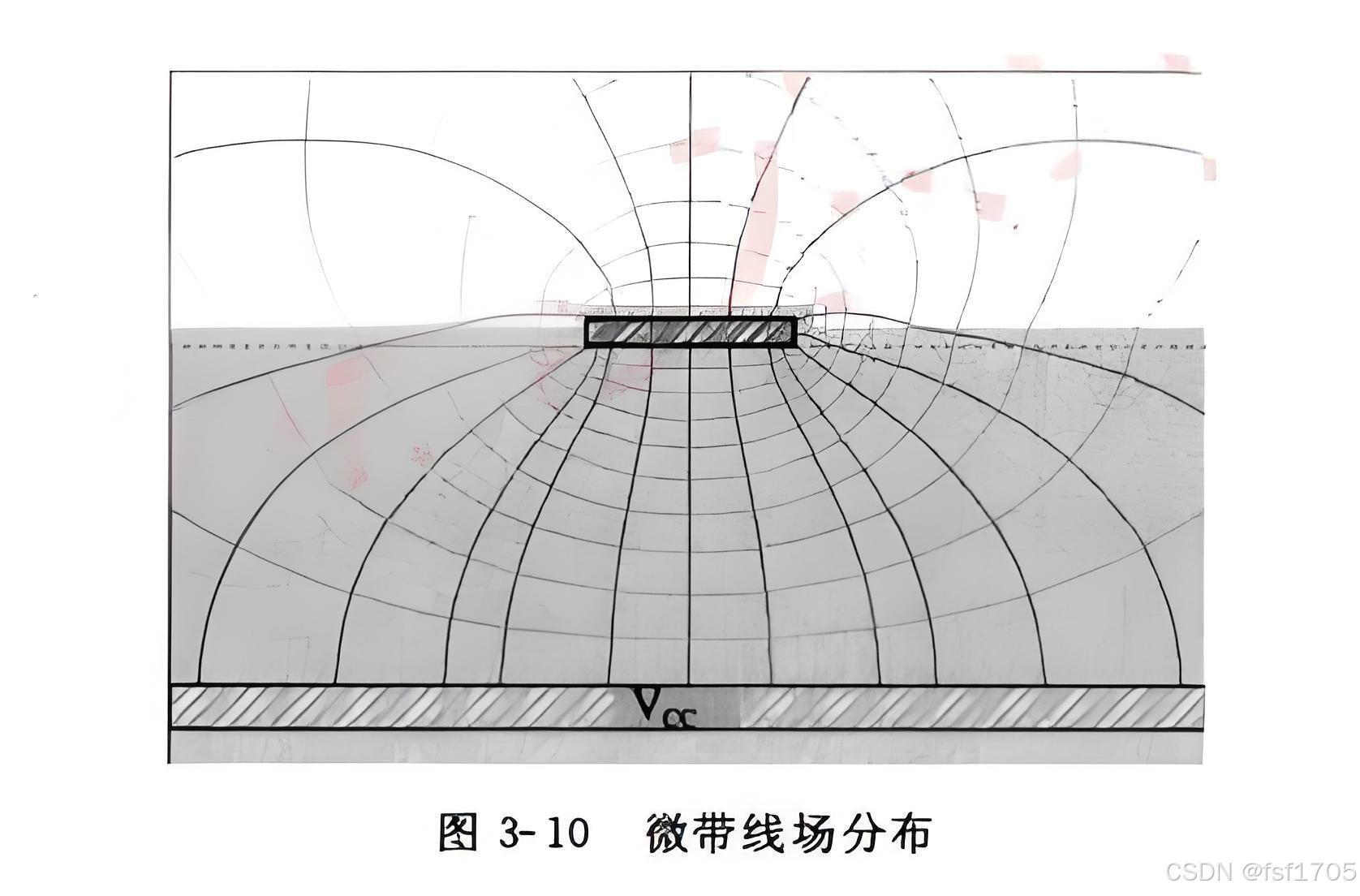
有关。此时可以使用等效介电常数e, 。一种典型的情况是PCB上的表层走线，走线的

一边是空气，另一边是PCB板材，电力线一部分分布在空气中，另一部分分布在板材中，如

图3-10所示。因此，表层走线“感受”到的介电常数必然是空气和介质的某种平均。空气

的介电常数为1,小于板材的介电常数，表层走线“感受”到的等效介电常数就小于板材的

介电常数。假设走线为50Ω阻抗控制的表层走线，线宽为6mil,介质的介电常数为4.4,

则走线“感受”到的等效介电常数为3.44。很难用近似公式准确地估计等效介电常数的数

值，要想了解等效介电常数的大小，最好的办法就是使用场求解器，很多场求解器都可以准

确地计算出等效介电常数。