闲谈NP

本文扯了扯P，NP，NP-c，NP-hard。作为一个调节，过两天再聊linux。

先来看一个小故事，假如老板要你解决一个问题，你绞尽脑汁还是想不出来，叫天天不应，叫地地不灵，这时你走进老板办公室，可以采取3种策略：

(1)

一副倒霉像，神情ws，可怜巴巴的说：老板，我没做出来，我想我是太蠢了。。。

boss：蠢材！滚！

(失败。。。)

(2)

雄赳赳气昂昂跨进老板办公室，大吼一声：小样，你丫给我问题根本就无解，害我白想这么些天，我靠！

boss：我才靠，自己做不出来就说这个问题无解，要是人人都这样混，我这老板还当个屁阿，滚！

(做不出来还如此气概，不仅失败，而且欠扁。。。)

(3)

从容不迫的说：老板，我做不出来，但是，我敢肯定，那些大牛牛们也照样做不出来

boss：原来是这样，那也难为你了。

以上三副图虽然是一个笑话，但也可以为我们的生活研究提供一些思路和指导。当你面对一个问题解决不了时，那么就试图去证明别人也解决不了，这的确是一个偷懒逃避的好借口。我觉得P，NP，NP-c，NP-hard这些名称的出现，就是因为某些难问题，连CS的大牛们都解决不了，无可奈何之下，只好定义一堆东西，为自己找个理由，免得说自己太笨了 :)

言归正传，我们讨论的都是决策问题(说白了就是回答yes/no的问题)，把决策问题按照难易程度分为几类：

(1)P问题。

定义：那些可以在多项式( polynomial )时间内解决的问题，称为P问题。(以后把"多项式时间"，简写为P时间)。时间复杂度如(n^2, n^4,  n(log(n)))都是P时间的，指数级别的如(2^n，n^n)这些就不是P时间了。一个算法的时间复杂度是P时间，哪怕是(n^100)，我们都称这个算法是有效率 effecient 的。

如最大公约数(gcd)，最短路径。但是还有很多问题我们不知道如何在P时间之内解决，如哈密顿路径等等。

(2)NP问题。

定义：给定一个解，我们可以在P时间内检查他正确与否的决策问题，成为NP( Non-deterministic polynomial )问题。

比如，我要找一个图的哈密顿路径，随便给我一个解，我都可以在P时间内检查它是不是哈密顿路径。只要形如定义的问题，就是NP问题。所以，P问题是属于NP问题的，因为给定一个P问题，我可以在P时间内找到答案，那么任意给我一个解，我简单的比较解和答案是不是相同，就可以回答yes/no，整个时间是P，符合定义。

(3)NP-c问题。

有意思的东西来了，在NP问题这一个大类里面，包含了太多太多的问题，有的很简单，如P问题，有的很困难，如找哈密顿路径。我们必须把这些同志区别开来。所以就定义了NP-c问题。

定义：NP-c问题是这样的一类问题，首先他是属于NP的，而且他是NP问题里面最难解决的问题。难到什么程度？只要其中某个问题可以在P时间内解决，那么所有的NP问题就都可以在P时间内解决了。

NP-c问题的定义出来了，但是，它忽悠了半天，除了说明这类问题比较难之外，其他啥也没有。我们还是不知道到底什么问题是NP-c问题，如何判定一个问题是不是NP-c问题。

1970年，太阳出来了，十月革命一声炮响，cook同志发明了cook定理，找到了第一个NP-c问题，SAT(Satisfiability)问题。他是这么说的，如果SAT问题可以在P时间解决，那么所有的NP问题都可以在P时间内解决。

我靠，现在好了，我们知道了一个NP-c问题，下面的问题就好办了，要判断一个问题 Q 是不是相当难问题，是不是一个NP-c问题。那么我们要做的事情就是，第一步，判断Q是不是NP（这好办），第二步，判断Q这个问题的难度是不是比cook同志提出来的SAT问题还要难，如果Q比SAT问题还难，我靠，没希望了，丫肯定是NP-c。。。

判断两个问题Q，R的难易程度，我们可以这么来做。具体的套路叫做多项式归约(polynomial time reduction)，意思是，我们要解决R，但是我们可以先把问题在多项式时间内转化成Q问题，只要解决了Q问题，R问题就解决了。如果问题R可以多项式归约到Q，那么Q一定不比R容易。记为R<=Q。

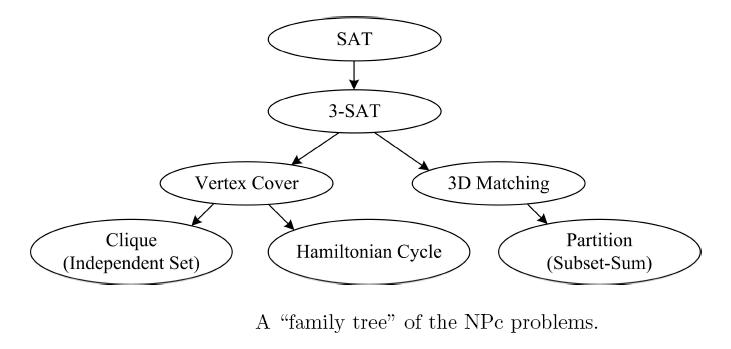
好了，我们就可以从第一个NP-c问题出发，一层一层的把问题转化下去，形成了NP-c问题的树。(这些问题的相互转化，很有意思，相当精彩！)

(4)NP-hard问题。

定义：NP-hard问题是这样的问题，只要其中某个问题可以在P时间内解决，那么所有的NP问题就都可以在P时间内解决了。NP-c问题就是NP-hard问题。但注意NP-hard问题它不一定是NP问题，比如，下围棋就是NP-hard问题，但不是NP问题，我们要在一个残局上找一个必胜下法，告诉我们下一步下在哪里。显然，我们找不这个解，而且更难的是，就算有人给我了一个解，我们也无法在P时间内判断它是不是正确的。

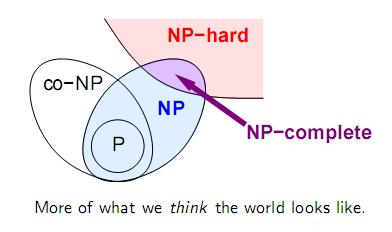
现在普遍认为这些问题的关系是这样的：(CO-NP和NP差不多)

最后，P==NP?，鬼才知道。

 

by - 复旦人乙