LeetCode 2304. 网格中的最小路径代价

原题链接：. - 力扣（LeetCode）

给你一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1) 中的任何一个单元格。注意： 在最后一行中的单元格不能触发移动。

每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m * n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。

grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

示例 1：

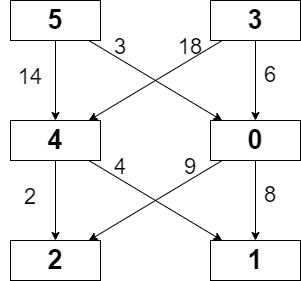
输入：grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出：17
解释：最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。

示例 2：

输入：grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出：6
解释：
最小代价的路径是 2 -> 3 。 
- 路径途经单元格值之和 2 + 3 = 5 。 
- 从 2 移动到 3 的代价为 1 。 
路径总代价为 5 + 1 = 6 。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• grid 由从 0 到 m * n - 1 的不同整数组成
• moveCost.length == m * n
• moveCost[i].length == n
• 1 <= moveCost[i][j] <= 100

思路：

采用递归的思路解决。定义 dfs(grid,i,j,moveCost) 为从 [ i, j ] 出发到达最后一行所需要的最小的代价。对于一个 节点[ i，j ]，可以移动第 i +1 行的任一列节点 x[ i+1 ,k ] ，取出 [ i, j ] 到 节点 x 的代价 moveCost[ grid[ i ][ j ]][ k ] 与 节点 x 到最后一行的代价 dfs(grid,i+1,k,moveCost) 的和的最小值 ，再加上节点[ i ,j ] 自身的价值 grid [ i , j ], 即是 从[ i, j ] 到达最后一行所需要的最小的代价值。同时还引入了 memo 数组将已经计算过的节点的最小的代价保存起来，避免重复计算。

代码：

class Solution {
    int[][] memo;
    public int minPathCost(int[][] grid, int[][] moveCost) {
        int m = moveCost.length, n = moveCost[0].length;
        memo = new int[m][n];
        int res = Integer.MAX_VALUE;
        for(int j=0;j<n;j++){
            res = Math.min(res,dfs(grid,0,j,moveCost));
        }
        return res;
    }
    //dfs(grid,i,j,moveCost)返回从[i,j]出发的最小路径代价
    int dfs(int[][] grid,int i,int j,int[][] moveCost){
        //到达递归边界
        if(i== grid.length-1){
            return grid[i][j];
        }
        //从最后一行的任一节点[i,j]出发的最小路径代价是grid[i][j]
        if(memo[i][j] != 0){
            return memo[i][j];
        }
        int res = Integer.MAX_VALUE;
        for(int k=0;k<grid[0].length;k++){
            res = Math.min(res,dfs(grid,i+1,k,moveCost)+ moveCost[grid[i][j]][k]) ;
        }
        return memo[i][j] = res + grid[i][j];
    }
}

参考：. - 力扣（LeetCode）