
均值:
input=np.array([92,94,103,105,106])
np.mean(input)100.0
子样方差:
np.dot((input-mean_number),(input-mean_number))/534.0

X=np.array([1,3,6,26])
N=np.array([8,40,10,2])
def get_mean(X,N):
sum=0
length=0
for i in range(len(X)):
sum = sum + X[i]*N[i]
length=length+N[i]
return sum/length
def get_variance(X,N):
D_value=np.array([])
length=0
for i in arange(len(N)):
length=length+N[i]
for j in arange(N[i]):
D_value = np.append(D_value,(get_mean(X,N)-X[i])**2)
pass
pass
return np.sqrt(np.sum(D_value)/length)得到平均值:4.0
得到标准差:4.320493798938574
得到方差:18.666666666666668

顺序统计量:
array_number=np.array([-2.1,3.2,0,-0.1,1.2,-4,2.22,2.01,1.2,-0.1,3.21,-2.1,0])
array_number=np.sort(array_number)
array_number
array([-4. , -2.1 , -2.1 , -0.1 , -0.1 , 0. , 0. , 1.2 , 1.2 ,
2.01, 2.22, 3.2 , 3.21])
中位数
len(array_number)13
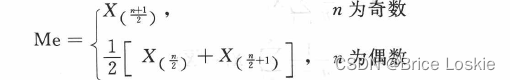
Me=array_number[int((len(array_number)+1)/2)]
Me极差:7.21
array_number[-1]-array_number[0]插入2.7之后的中位数:0.6
array_number=np.append(array_number,2.7)
array_number=np.sort(array_number)
len(array_number)
n=len(array_number)
left=array_number[int(n/2)-1]
right=array_number[int(n/2)]
Me=(right+left)*0.5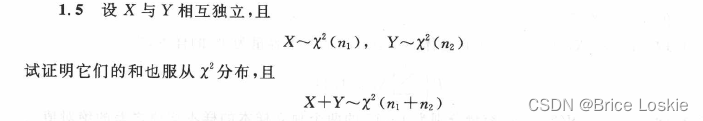

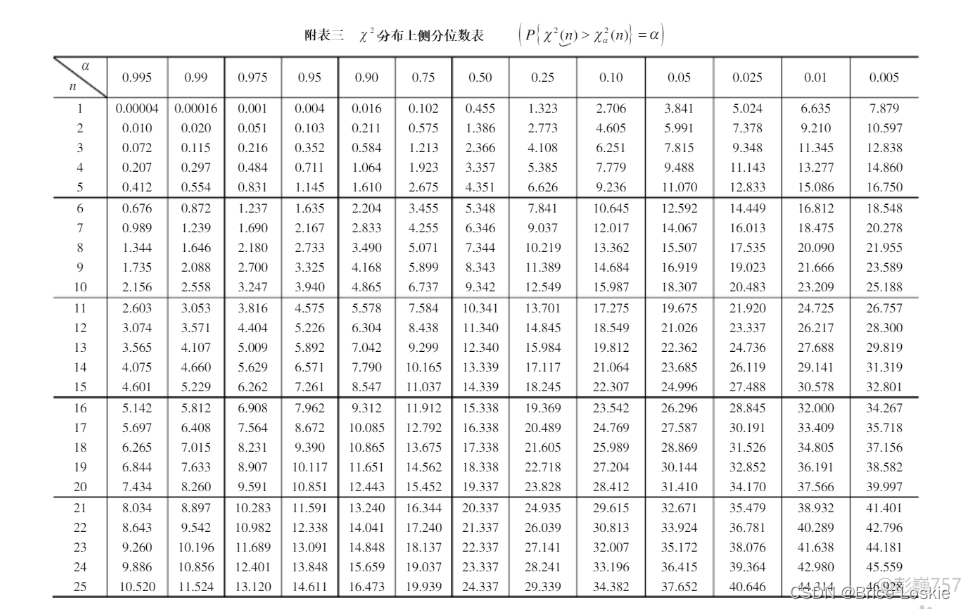
由卡方分布的定义:
满足卡方分布的定义 上面的式子成立

两个式子合并之后:

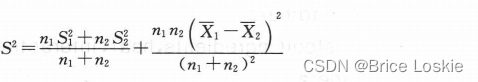
公式的推导,运算大家慢慢计算。

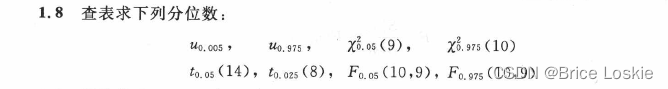
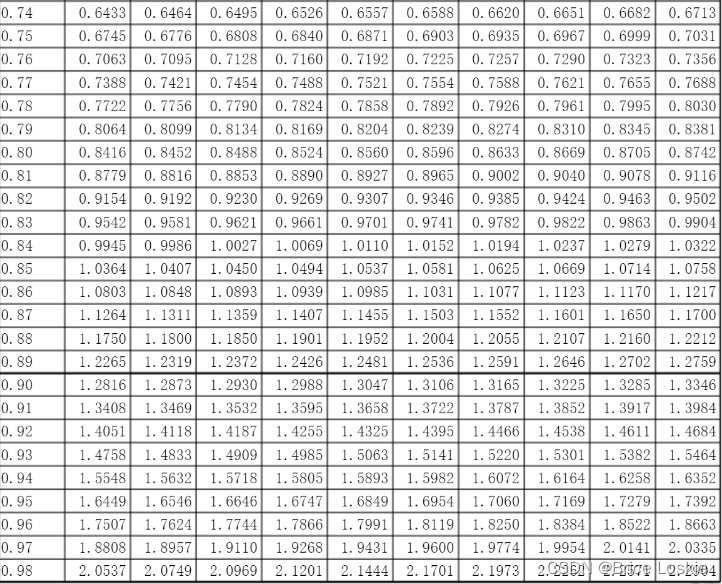
我们先把表复制过来:
查表自己查 老火得很
正态分布:=表上找不到0.005或者0.995所以找不到
=-1.96

卡方分布:
=16.919
=3.25
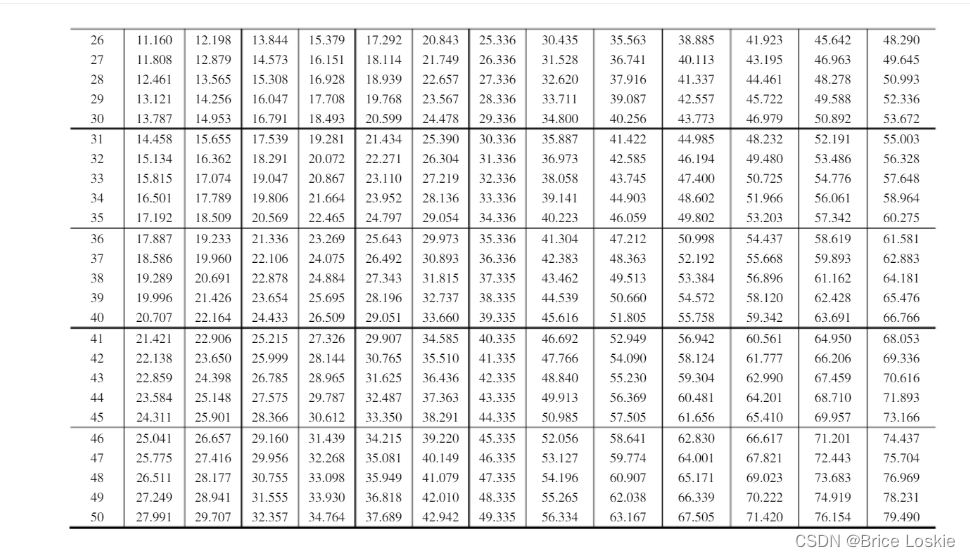
=1.761
=2.306

=3.02
=1/3.78=0.2645502645502646
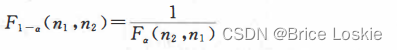
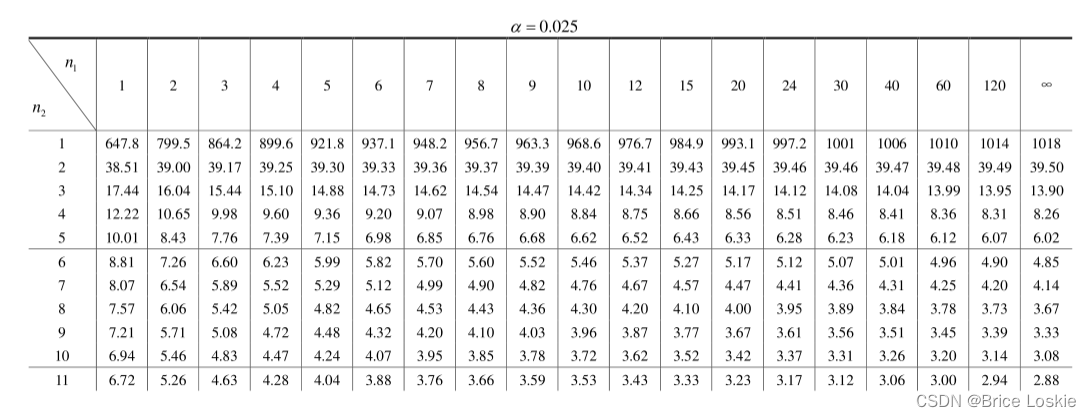
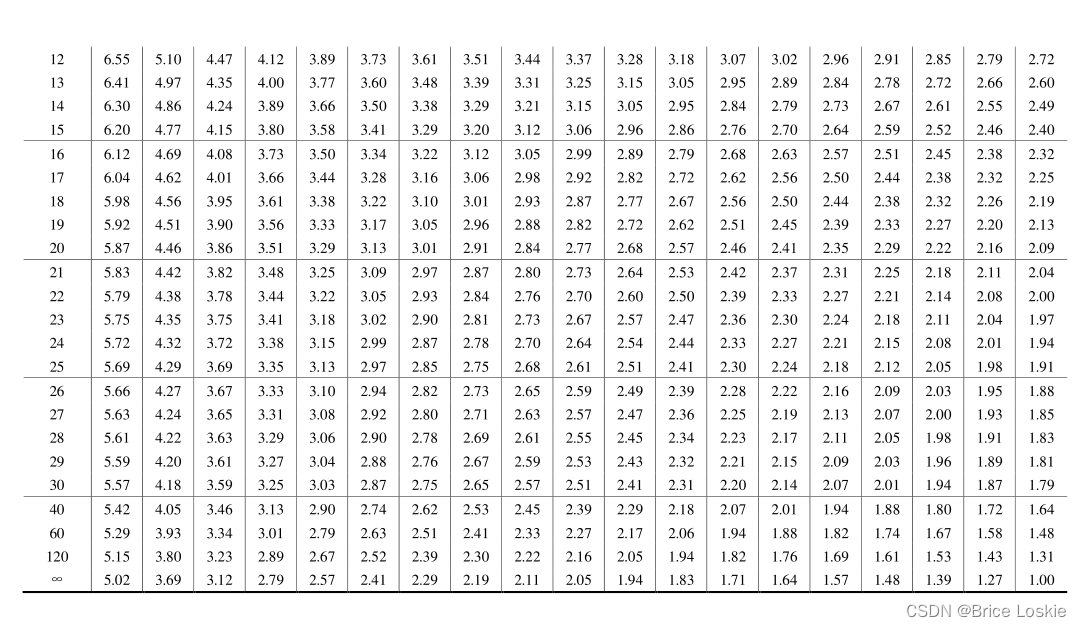
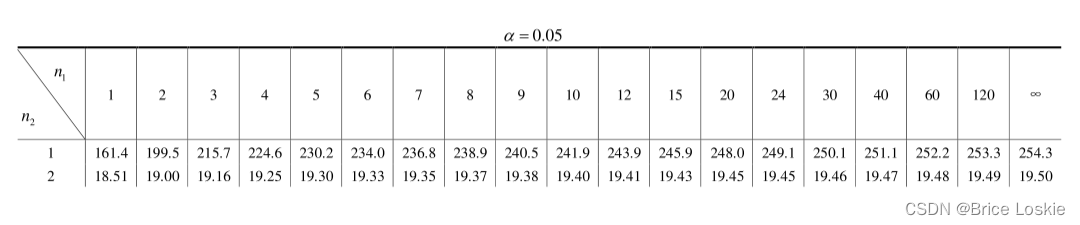
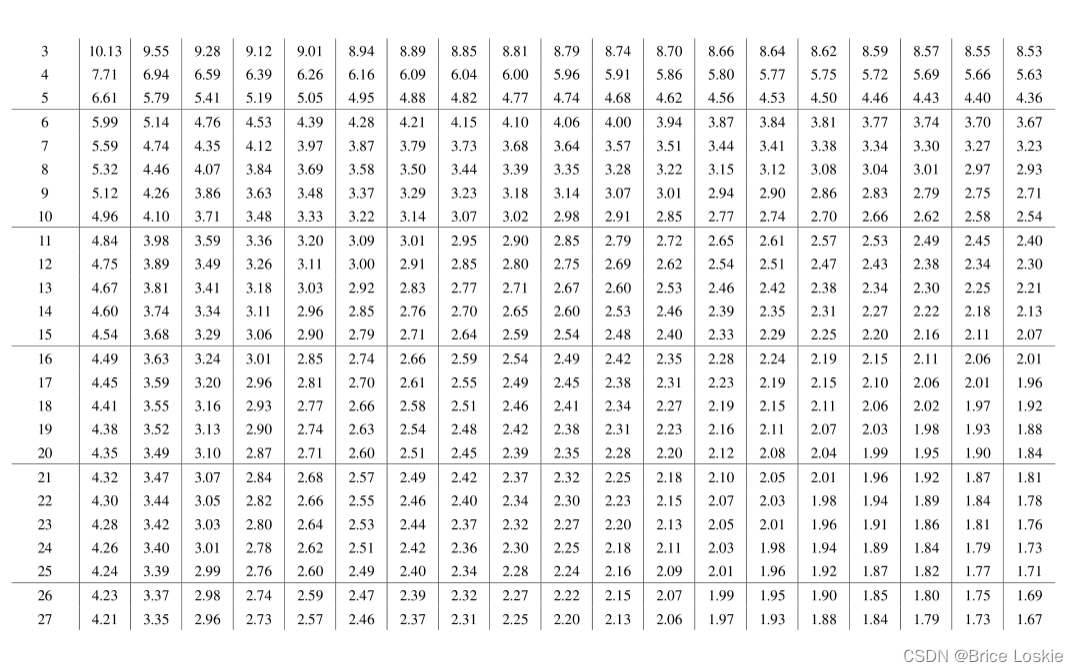
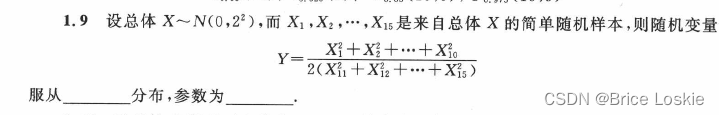
F n2=10 n1=5

补充:正态分布的可加性:
带入此式子:
此时我们只需要把和
标准正太化即可满足卡方分布
正态分布标准化:
为非正态分布,则
为标准正态分布.
即统计量减期望值后除以方差.
此时我们只需要除以
即
现在我们可以看出当C=1/3可以办到
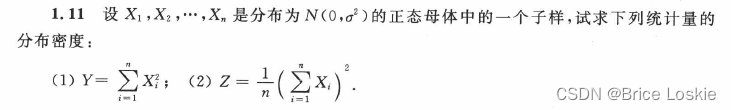
我们需要看一下非标准的正态分布张啥样
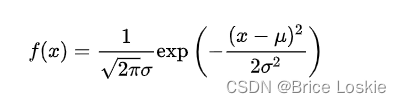
N(0,σ^2)的密度函数为
得到
再来看看卡方分布的密度函数
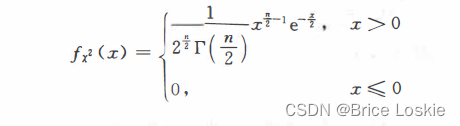
答案:

这个证明推导不出来 有点难度 ,跳过,不过花个半天应该可以推导出来 ,太麻烦了 算求了
![]()
第一个式子满足t分布,自由度为n
第二个式子满足F分布,自由度为1,n
t分布的式子

F分布的式子

X^2满足卡方分布 此时自由度为1
所以 此式子成立

![]()
我们先找到近似计算公式:
![]()
带入a=0.01 n=90
这是什么题喔 主要式查表查不到,如果查到了带入即可 我们可以找规律来估算大概等于2.3
np.sqrt(180)*2.3+90估算答案:120.8577380894971

由于
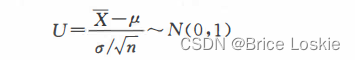
要求
则我们需要求
我们需要查表=1.5时候 P0.9335 由于表上我们弄的下册分位数 ,所以我们需要1-0.9335=0.0665
由于我们求的式绝对值 则需要乘以2
最后结果约为:0.130
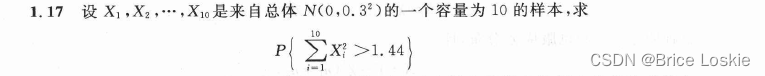
我们需要将X做标准化转换即
服从卡方分布
即: 服从卡方分布
 转换为
转换为
自由度为10 我们查表得到的概率与等于0.10

我们需要带入如下公式进行计算:
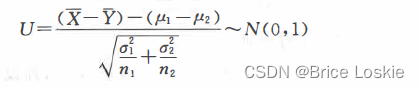
先求的概率
我们找到小于0.225的概率为0.589
大于0.225的概率为0.411
我们求的式绝对值 综上 结果为0.822
结果不一样 我怀疑式哪里做错了 操





















 23万+
23万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








