哈夫曼树

最新推荐文章于 2023-11-19 11:00:25 发布

搞么子啊小子

最新推荐文章于 2023-11-19 11:00:25 发布

阅读量1.5k

点赞数 3

树专栏收录该内容

5 篇文章 0 订阅

订阅专栏

一、哈夫曼树的概念和定义

哈夫曼树有关的概念：

路径：树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。

路径长度：路径上的分枝数目称作路径长度。

树的路径长度：从树根到每一个结点的路径长度之和。

结点的带权路径长度：在一棵树中，如果其结点上附带有一个权值，通常把该结点的路径长度与该结点上的权值之积称为该结点的带权路径长度（weighted path length）

树的带权路径长度：如果树中每个叶子上都带有一个权值，则把树中所有叶子的带权路径长度之和称为树的带权路径长度。

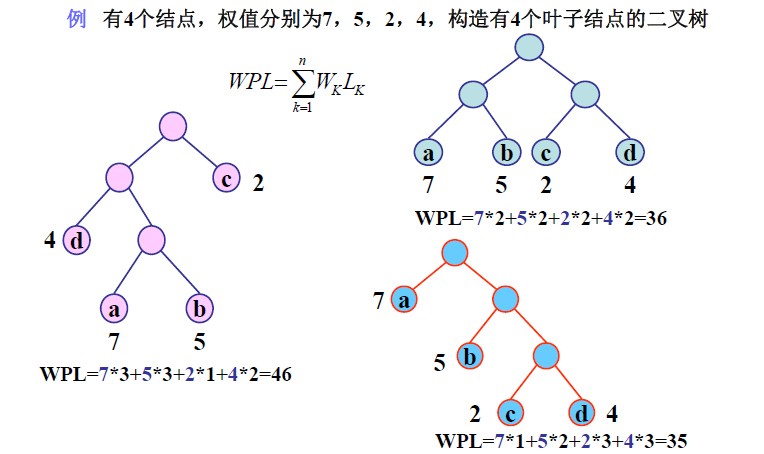
其中带权路径长度最小的二叉树就称为哈夫曼树或最优二叉树

===============================================================================

二、哈夫曼树的构造

根据哈弗曼树的定义，一棵二叉树要使其WPL值最小，必须使权值越大的叶子结点越靠近根结点，而权值越小的叶子结点

越远离根结点。

哈弗曼依据这一特点提出了一种构造最优二叉树的方法，其基本思想如下：

下面演示了用Huffman算法构造一棵Huffman树的过程：

算法实现：

#include<iostream>
#define M 1000
using namespace std;
int n,m;

struct node
{
	float weight;			//定义权重
	int parent;				//定义双亲在向量中的下标
	int lchild,rchild;		//定义左右子树
}T[M];

//哈夫曼树的构造
void huffman()
{
	int i,j,p1,p2;
	float small1,small2;

	for(i=n+1;i<=m;i++)		//进行n-1次合并，产生n-1个新结点
	{
		p1=p2=0;
		small1=small2=M;
		for(j=1;j<i;j++)
		{
			if(T[j].parent!=0) continue;    //不考虑已合并过的点
			if(T[j].weight<small1)			//修改最小权和次小权及位置
			{
				small2=small1;
				small1=T[j].weight;

				p2=p1;
                p1=j;
			}
			else if(T[j].weight<small2)		//修改次小权及位置
			{
				small2=T[j].weight;
				p2=j;
			}
		}

		T[p1].parent=T[p2].parent=i;		//新根
		T[i].parent=0;      
		T[i].lchild=p1;    // 新节点左儿子
		T[i].rchild=p2;    // 新节点右儿子
		T[i].weight=small1+small2;			//新结点的权值为最小权与次小权之和
	}
}

int main()
{
    int i;
    while(cin>>n)
    {
      m=2*n-1;
      for(i=1;i<=n;i++)
      {
        cin>>T[i].weight;
		T[i].parent=0;		        //无双亲，即为根结点，尚未合并过
		T[i].lchild=T[i].rchild=0;  //左右孩子指针置为0
      }

	  huffman();
	  for(int i=n+1;i<=m;i++)
		cout<<T[i].weight<<" ";
      cout<<endl;
    }
	return 0;
}

=============================================================================

三、哈夫曼树的在编码中的应用

1. 等长编码

这种编码方式的特点是每个字符的编码长度相同（编码长度就是每个编码所含的二进制位数）。假设字符集只含有4个字符A，B，C，D，用二进制两位表示的编码分别为00，01，10，11。若现在有一段电文为：ABACCDA，则应发送二进制序列：00010010101100，总长度为14位。当接收方接收到这段电文后，将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性，但编码长度并不是最短的。

2. 不等长编码

在传送电文时，为了使其二进制位数尽可能地少，可以将每个字符的编码设计为不等长的，使用频度较高的字符分配一个相对比较短的编码，使用频度较低的字符分配一个比较长的编码。例如，可以为A，B，C，D四个字符分别分配0，00，1，01，并可将上述电文用二进制序列：000011010发送，其长度只有9个二进制位，但随之带来了一个问题，接收方接到这段电文后无法进行译码，因为无法断定前面4个0是4个A，1个B、2个A，还是2个B，即译码不唯一，因此这种编码方法不可使用。

因此，为了设计长短不等的编码，以便减少电文的总长，还必须考虑编码的唯一性，即在建立不等长编码时必须使任何一个字符的编码都不是另一个字符的前缀，这种编码称为前缀编码（prefix code）

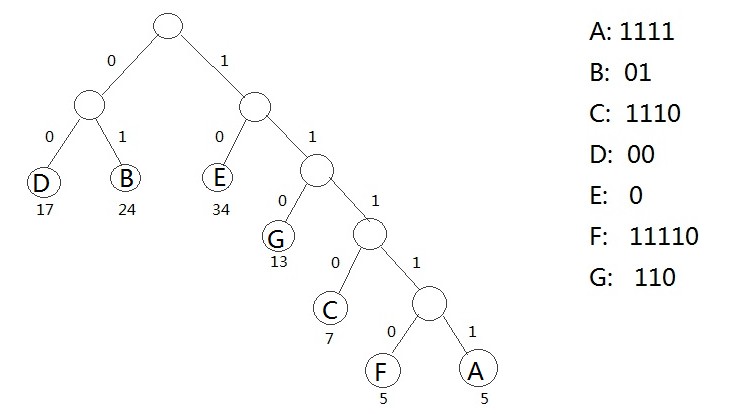
1.利用字符集中每个字符的使用频率作为权值构造一个哈夫曼树；

2.从根结点开始，为到每个叶子结点路径上的左分支赋予0，右分支赋予1，并从根到叶子方向形成该叶子结点的编码

通过哈夫曼树来构造的编码称为哈弗曼编码（huffman code）