ML - SVM

SVM

提出问题

分类学习最基本的想法就是基于训练集D在样本空间找到一个超平面，将不同类别的样本分开。但是划分超平面的可能性有很多，该如何寻找？

划分超平面的线性方程描述：

$w^{T}x+b=0$

在二维空间，这个discriminant是line，3-D: plane, m-D: hyperplane.

我们要找的就是Maximum margin，这个最大间隔可以这样确定：选两个能够正确分类的平行的超平面，使他们之间的间隔越大越好。然后我们选择这两个超平面中间的超平面作为最优解，因为它最为鲁棒，泛化能力最强。

寻找最优解

在这两个超平面上的样本点就是支持向量(support vector)

那怎么确定是否正确分类？

空间一点到任一超平面的距离：
$$r=\frac{|{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b|}{\Vert w\Vert }$$
这里$$\Vert w\Vert$$是L2范数

如果超平面(w,x) 分类正确，那么，对于样本空间的任一样本点$$(x_i,y_i)$$有

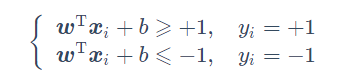
这个是可以推的，大概是，对于正类超平面方程大于等于某个正常数，对于负类小于等于某个负常数，两边同除以常数，方程右边就变成1了，再对w，b做一些缩放变换。只要能正确分类，肯定有这样的缩放。

再说一句，这两个方程的目的是帮我们确定支持向量

所以，两个异类的支持向量到我们理想超平面的距离和，也就是上文说的margin

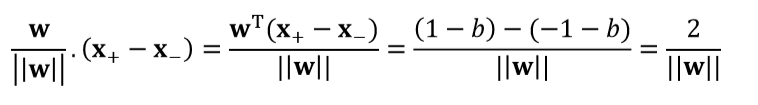
当然可以，把一个超平面上的支持向量代到另一个超平面的上述距离公式中，得到一样结果。

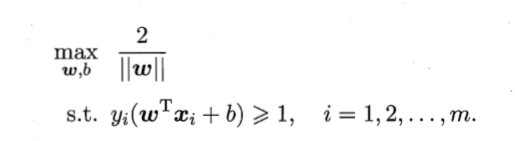
这就是我们要努力的方向，当然，可以变换为

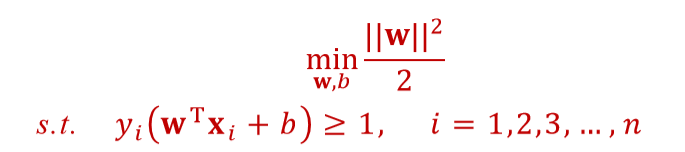
这就是Basic Support Vector Machine

求解

我们已经确定了需要求解的目标和与之对应的约束条件，接下来就是求解了。

这本身是一个凸二次规划问题已经可以调用现成的优化计算包解决。How?

不过有着更为高效的方法。我们可以采用拉格朗日乘子法计算其对偶问题，在计算过程中，需要记得满足KKT（Karush-Kuhn-Tuncker)，这里我们先略过，毕竟，我不想刚入门就放弃。

拉格朗日乘子法

详细过程参考周志华《机器学习》附录B优化部分。
拉格朗日乘子法可以将有条件的求极值转换为无条件的求极值的方法。
即如果原来有d个变量，k个约束条件，我们可以转化为有d+k个变量的无约束的优化问题求解。
原理是约束曲面上的任意点的梯度正交约束曲面，而目标函数在该点的梯度同样正交约束曲面。可以通过这个条件来列出拉格朗日函数。

对偶问题

对一个优化问题，可以从两个角度来考察，一个是主问题（primal problem)和对偶问题（dual problem）
这里没看懂，先记住结论，当强对偶性成立时，对偶问题解决，主问题也解决。

数学推导

套用拉格朗日函数后的方程，如下，其中乘子记为a，

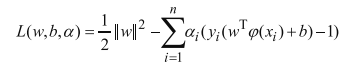
然后借助KKT条件，

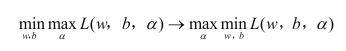
接下来求极值，让w，b的偏导等于零

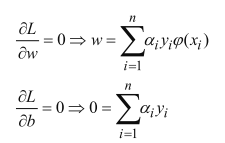
现在这个问题，就和引入的乘子a挂钩了，而且可以把w，b统统用a来表示，所以代回拉格朗日函数就是

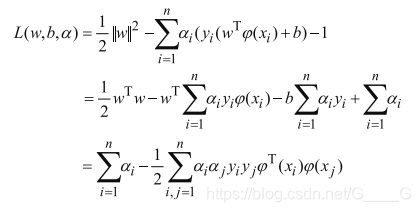
现在就是在求，a值为多少，了L(w,b,a)的值最大，然后我们得到了

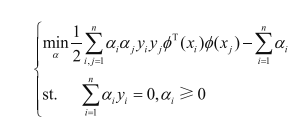
这个就是上面标红的支持向量机的基本型的对偶问题（dual problem)

求解出a，就可以求除w，b得到模型。
那如何求解上面这个式子呢？
首先，这是一个二次规划问题，可以使用通用的二次规划算法求解，但是训练样本数的上升会对实际问题造成很大开销。为了解决这个问题，有很多高校算法被提出，其中就有SMO(Sequential Minimal Optimization)

SMO

略

软间隔

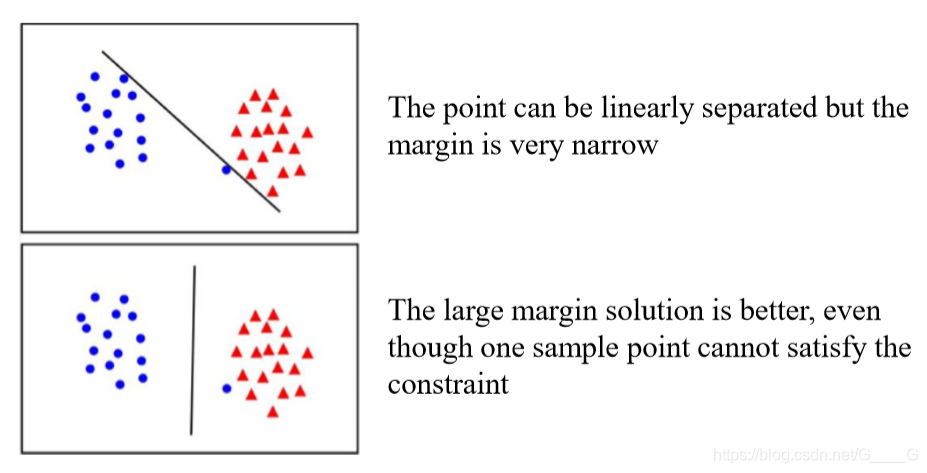
我们之前谈论的都是线性可分的情况，事实上如果严格划分会过拟合，通常在间隔和误差之间我们需要trade-off.通常我们的数据都不是linearly separable的。所以我们可以采用Relaxed Formulation，引入一个slack variable这样我们就允许一些错误的出现，就是软间隔（soft margin)

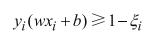
来放低要求，这样新的目标函数就定义为：

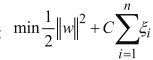
这个的参数C就是严格程度。

1. 假如C趋于无穷，那么只有当ξ非常小才能得到整体的极小值，这样ξ需要趋于0，又回到了硬间隔的情况
2. 假如C趋于0，那么ξ可以大一些，意味着模型可以容忍更多的误差。
   在目标函数增加了新的项，求解过程没有太大变化，还是套用拉格朗日函数，求对偶问题，同时要满足KKT条件要求
   软间隔拉格朗日函数：
   
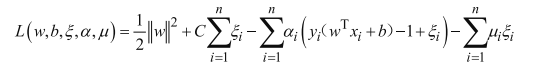
   对偶问题：
   

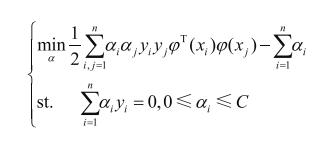
核函数

PCA是个好东西，可以帮我们找到更好的代表特征。
不过上文也提到了，在原始样本空间内找不到划分两类样本的超平面怎么办？那我们可以把样本，从原始空间映射到更高维的特征空间，就是降维的逆过程，升维。利用高维数据来重新划分样本空间。
假如∮(x)是x映射到更高维特征空间的特征向量，那么新的特征空间中划分超平面所对应的模型可以表示为：

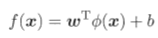
对于这样的试子，我们已经可以直接当作基本型来求解。
但是在求解过程中，会与到一个问题，就是特征空间维数可能很高，甚至无穷维，所以计算升维后特征向量的内积的计算很困难。
为什么会很困难呢？
假如我们有三维空间的两个数据点，但在三位空间中不能对他们划分，我们通过函数∮(x)映射到高为空间，假如映射到100维空间，在变换后我们还要进行100次内积计算。这是只有两个样本点，那要是100万个样本点，求两两内积怎么办？
我们可以假设有这样一个函数，输入是原始样本空间中的样本点，输出为他们在特征空间的内积。这样的函数我们称为核函数(kernel function)
如果我们知道了映射函数∮(x)，核函数就可以确定。可以证明，对于一个半正定核矩阵，总能找到一个与之对应的映射∮.

通常我们是不知道特征映射的形式的，这样我们就不知道选择什么核函数是合适的，而核函数也仅能隐式的定义这个特征空间。所以**“核函数的选择”对于支持向量机而言是很关键**。

而事实上，将数据投影到高维空间是一个假设，我们只要在低维空间求出内积在把结果映射到高维空间就可以了。这样子我们获得更多的特征信息的同时，计算复杂度没有发生本质改变。

在实际应用支持向量机的过程中，最常使用的是高斯核函数：

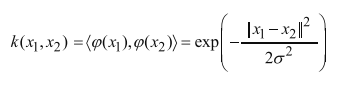
还有一些其他的核函数，也可以对和杉树做组合获得新的核函数，但都不如高斯核函数常用，

SVM实际应用中参数的选择

1.首先就是松弛变量ξ，这由C来控制,上文提到了，C越大分类越严格，对错误的容忍越低。这个具体数值需要通过实验判断。
2.是高斯核函数中的分母中的变量σ，这个值决定了数据变换，进而控制模型的复杂程度。σ越大，模型的复杂度越高。而模型复杂度过高，就会存在过拟合的风险。通常我们希望模型不要太复杂，保持较强的泛化能力，以更好的处理实际任务，不过具体值和C一样， 选择0.1还是10要交叉验证对比分析后才能知道。