蛇形三角填数

描述

跟蛇形填数一样，只是填数要求按照三角形填。注意每组数据之间用空行隔开

输入

第一行有一个N，表示N组测试数据
接下来每组数据包括一个数字X，表示三角形的边长，0< X <1000

输出

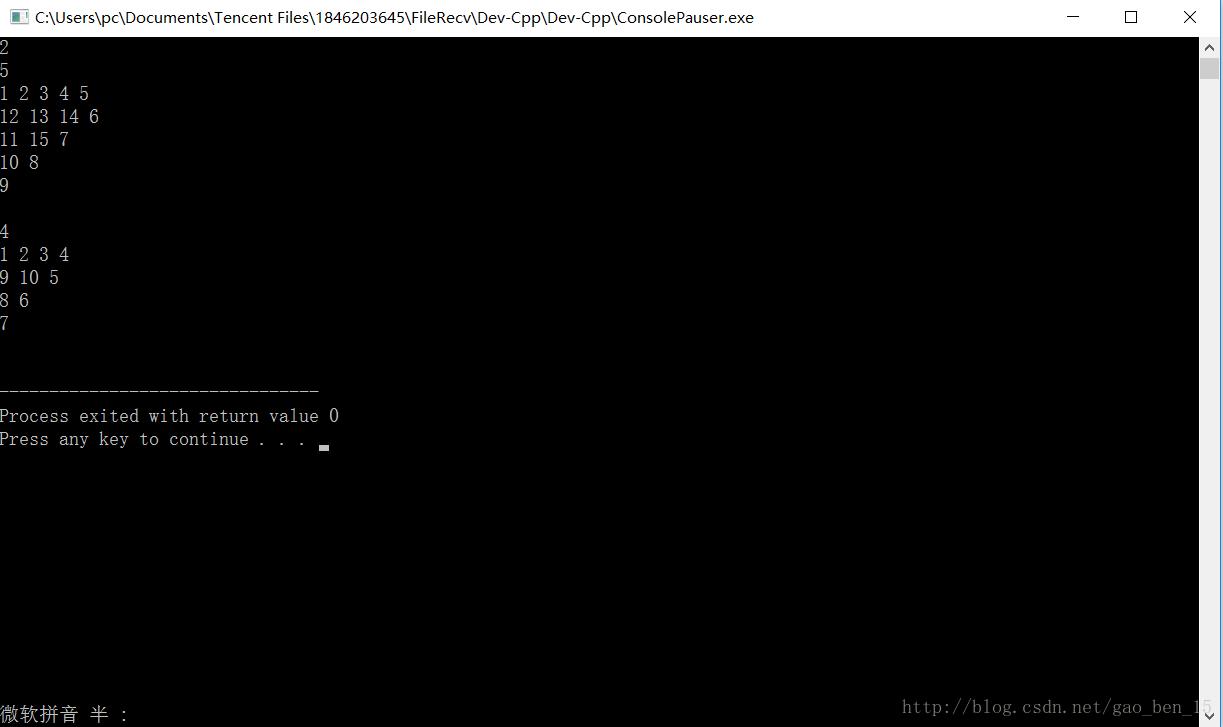
输出之后填好之后的图

解题思路

首先找出图形的特点(对称性等)与循环变量(行号,列号)之间的关系. 我们可以假设行用i表示,列用j表示.我们的目的就是找出i,j与图形之间的对应关系.按图形形状的不同,复杂性不同.但是都可以看做是在寻找一种或多种”静态关系”. 蛇形填数这种题目的思路就是找出题目中对图形的限制条件(不能出界,按照一定规则填充等).我们用各种循环和If语句将这些”规则”变成程序语句.同样,根据”规则”不同,复杂性也不同.但是都可以看做是在寻找一种或多种”动态关系”.明确了解题思想不同后,因此我们要寻找的就是”动态关系”.这里的动态关系就是”蛇形”.通过观察,我们可以看出规则:在规定的方阵n*n里.在不越界及不走重复位置的前提下,填充元素遵循右下左上的规定.即向右走到顶后向下走到顶,再向左走到顶,向上走到顶. 现在我们就将规则变成程序语句.首先是怎么样判断不越界.由于方阵是n*n的方阵,我们使用二维数组最大元素是a[n-1][n-1].那判断是否行越界是不是就用语句if(y <= n-1)就行了呢? 思路上是没错,不过具体实现时会遇到麻烦,因为当y <= n-1的时候是要不停地进行y+