深入浅出统计学 笔记 总结 学习心得
数据集中趋势
均值、众数、中位数
μ
=
∑
x
n
\mu=\frac{\sum x}{n}
μ=n∑x
数据分散性
极差(全距)
x
m
a
x
−
x
m
i
n
x_{max}-x_{min}
xmax−xmin
四分位数【第[一|二|三|四]四分位,四分位距【第三-第一四分位距】】
1.5倍IQR(IQR=三分位数-一分位数)
数据差异性
方差:度量数据分散性。
σ
2
=
∑
(
x
−
μ
)
2
n
=
∑
x
2
n
−
μ
2
\sigma^2=\frac{\sum(x-\mu)^2}{n}=\frac{\sum x^2}{n} - \mu^2
σ2=n∑(x−μ)2=n∑x2−μ2
标准差:
σ
\sigma
σ
标准分(Z分):是一种由原始分推导出来的相对地位量数,用来说明原始分在所属的那批分数中的相对位置
标准分的作用:将几个数据集转成一个可用于进行比较的均值为0,标准差为1的新的通用分部
z
=
x
−
μ
σ
z=\frac{x-\mu}{\sigma}
z=σx−μ
V
a
r
(
X
)
=
E
(
X
2
)
−
E
2
(
X
)
Var(X)=E(X^2)-E^2(X)
Var(X)=E(X2)−E2(X)
概率:度量某事发生几率的一种数量指
事件:人们能够发出其发生可能性的任何事
发生事件A的概率:
P
(
A
)
=
n
(
A
)
n
(
S
)
P(A)=\frac{n(A)}{n(S)}
P(A)=n(S)n(A)
n(A):发生事件A的可能
n(S):所有可能结果的数目S称为:概率空间(样本空间)
P
(
A
∣
B
)
=
P
(
A
∩
B
)
P
(
B
)
P
(
A
∩
B
)
=
P
(
A
∣
B
)
×
P
(
B
)
P(A|B)=\frac{P(A \cap B)}{P(B)} \\P(A \cap B)=P(A|B)\times P(B)
P(A∣B)=P(B)P(A∩B)P(A∩B)=P(A∣B)×P(B)
全概率公式:
P
(
B
)
=
P
(
A
)
×
P
(
B
∣
A
)
+
P
(
A
‘
)
×
P
(
B
∣
A
‘
)
P(B)=P(A) \times P(B|A) + P(A^`) \times P(B|A^`)
P(B)=P(A)×P(B∣A)+P(A‘)×P(B∣A‘)
贝叶斯定理
P
(
A
∣
B
)
=
P
(
A
)
×
P
(
B
∣
A
)
P
(
A
)
×
P
(
B
∣
A
)
+
P
(
A
‘
)
×
P
(
B
∣
A
‘
)
P(A|B)=\frac{P(A) \times P(B|A)}{P(A) \times P(B|A) + P(A^`) \times P(B|A^`)}
P(A∣B)=P(A)×P(B∣A)+P(A‘)×P(B∣A‘)P(A)×P(B∣A)
P
(
A
∣
B
)
=
P
(
A
)
×
P
(
B
∣
A
)
P
(
B
)
P(A|B)=\frac{P(A) \times P(B|A)}{P(B)}
P(A∣B)=P(B)P(A)×P(B∣A)
相关事件
P
(
A
∣
B
)
≠
P
(
A
)
P(A|B) \neq P(A)
P(A∣B)=P(A)
独立事件
P
(
A
∣
B
)
=
P
(
A
)
P(A|B) = P(A)
P(A∣B)=P(A)
P
(
A
∩
B
)
=
P
(
A
)
×
P
(
B
)
P(A \cap B) = P(A) \times P(B)
P(A∩B)=P(A)×P(B)
期望:试验中每次可能结果的概率乘以其结果的总和
E
(
X
)
=
∑
x
P
(
X
=
x
)
E(X)=\sum xP(X=x)
E(X)=∑xP(X=x)
方差:
V
a
r
(
x
)
=
E
(
X
−
μ
)
2
=
∑
(
x
−
μ
)
2
P
(
X
=
x
)
\begin{aligned} Var(x)&=E(X-\mu)^2 \\ &=\sum(x-\mu)^2P(X=x) \end{aligned}
Var(x)=E(X−μ)2=∑(x−μ)2P(X=x)
E
(
a
x
+
b
)
=
a
E
(
x
)
+
b
E(ax+b)=aE(x)+b
E(ax+b)=aE(x)+b
V a r ( a x + b ) = a 2 V a r ( x ) Var(ax+b) = a^2Var(x) Var(ax+b)=a2Var(x)
E ( x 1 + x 2 + ⋅ ⋅ ⋅ + x n ) = n E ( x ) E(x_1+x_2+···+x_n)=nE(x) E(x1+x2+⋅⋅⋅+xn)=nE(x)
V a r ( x 1 + x 2 + ⋅ ⋅ ⋅ + x n ) = n V a r ( x ) Var(x_1+x_2+···+x_n)=nVar(x) Var(x1+x2+⋅⋅⋅+xn)=nVar(x)
排列组合
排列 A n r A_n^r Anr(也记作 P n r P_n^r Pnr):从n个不同的元素中,取r个不重复的元素,按次序排列,称为从n个中取r个的无重排列。A(n,r)。P(n,r)
A n r = n ( n − 1 ) ⋯ ( n − r + 1 ) = n ! ( n − r ) ! A_n^r = n(n-1)\cdots(n-r+1)=\frac{n!}{(n-r)!} Anr=n(n−1)⋯(n−r+1)=(n−r)!n!
组合
C
n
r
C_n^r
Cnr: 从n个不同元素中取r个元素,且不考虑顺序,称为从n个中取r个的组合,成为从n个中取r个的无重组合。
C
n
r
=
C
n
n
−
r
=
A
n
r
r
!
=
n
!
r
!
(
n
−
r
)
!
C_n^r=C_n^{n-r}=\frac{A_n^r}{r!}=\frac{n!}{r!(n-r)!}
Cnr=Cnn−r=r!Anr=r!(n−r)!n!
三个分布–离散型数据
几何分布:取得第一次成功需要的试验次数
X ∼ G e o ( p ) X\sim Geo(p) X∼Geo(p)
- 公式
P ( X = r ) = q r − 1 p P(X=r)=q^{r-1}p P(X=r)=qr−1p
p:单次成功的概率
q = 1-p(单次失败的概率)
- 期望
E ( X ) = 1 p E(X)=\frac{1}{p} E(X)=p1
- 方差
V a r ( X ) = q p 2 Var(X)=\frac{q}{p^2} Var(X)=p2q
- 不等式: P ( X > r ) P(X>r) P(X>r)指的是为了取得第一次成功需要试验r次以上的概率
P ( X > r ) = q r P(X>r)=q^r P(X>r)=qr
P
(
X
≤
r
)
=
1
−
q
r
P(X\leq r)=1-q^r
P(X≤r)=1−qr

二项分布:n次试验中事件A恰好发生p次的概率
X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p)
- 公式
P ( X = r ) = C n r p r q n − r P(X=r)=C_n^rp^rq^{n-r} P(X=r)=Cnrprqn−r
p = 0.5 , 图 形 堆 成 ; p > 0.5 , 图 形 左 偏 ; p < 0.5 , 图 形 右 边 p=0.5, 图形堆成;p>0.5, 图形左偏;p<0.5, 图形右边 p=0.5,图形堆成;p>0.5,图形左偏;p<0.5,图形右边
- 期望
E ( X ) = n p E(X)=np E(X)=np
- 方差
V
a
r
(
X
)
=
n
p
q
Var(X)=npq
Var(X)=npq

泊松分布: 适合于描述单位时间【面积、体积、空间等】内随机事件发生的次数。
X ∼ P o ( λ ) X \sim Po(\lambda) X∼Po(λ)
- 公式
P ( X = r ) = e − λ λ r r ! P(X=r)=\frac{e^{-\lambda}\lambda^r}{r!} P(X=r)=r!e−λλr
- 期望
E ( X ) = λ E(X)=\lambda E(X)=λ
- 方差
V a r ( X ) = λ Var(X)=\lambda Var(X)=λ
-
泊松分布二项分布
E ( B ( n , p ) ) = n p , V a r ( B ( n , p ) ) = n p q E(B(n,p))=np, Var(B(n,p))=npq E(B(n,p))=np,Var(B(n,p))=npq
E ( P o ( λ ) ) = λ , V a r ( P o ( λ ) ) = λ E(Po(\lambda))=\lambda, Var(Po(\lambda))=\lambda E(Po(λ))=λ,Var(Po(λ))=λ
当 n p = λ , 且 n p q = λ np=\lambda,且npq=\lambda np=λ,且npq=λ时,两者就近似替代了
即:当 n n n(如:大于50)很大,且 p p p(如小于0.1)很小时,二项分布和泊松分布近似
-
如果 X ∼ P o ( λ x ) X \sim Po(\lambda_x) X∼Po(λx)且 Y ∼ P o ( λ y ) Y \sim Po(\lambda_y) Y∼Po(λy), 则: X + Y ∼ P o ( λ x + λ y ) X+Y \sim Po(\lambda_x+\lambda_y) X+Y∼Po(λx+λy)

正态分布
X
∼
N
(
μ
,
σ
2
)
X \sim N(\mu,\sigma^2)
X∼N(μ,σ2)
X − μ σ ∼ N ( 0 , 1 ) \frac{X-\mu}{\sigma} \sim N(0,1) σX−μ∼N(0,1)
Z ∼ N ( 0 , 1 ) Z \sim N(0,1) Z∼N(0,1)查表的概率表示 P ( Z < x ) P(Z< x) P(Z<x)。如 P ( X < − 3.27 ) , 先 纵 轴 找 − 0.32 , 横 轴 找 0.07 P(X<-3.27),先纵轴找-0.32,横轴找0.07 P(X<−3.27),先纵轴找−0.32,横轴找0.07
找到的对应数值为 0.0005 0.0005 0.0005,则 P ( X < − 3.27 ) = 0.0005 P(X<-3.27)=0.0005 P(X<−3.27)=0.0005
P
(
Z
>
z
)
=
1
−
P
(
Z
<
z
)
P(Z>z)=1-P(Z<z)
P(Z>z)=1−P(Z<z),由于
任
意
一
点
z
的
P
(
Z
=
z
)
=
0
任意一点z的P(Z=z)=0
任意一点z的P(Z=z)=0,因此等式可以随意加入登号。
P
(
a
<
Z
<
b
)
=
P
(
Z
<
b
)
−
P
(
Z
<
a
)
P(a<Z<b)=P(Z<b)-P(Z<a)
P(a<Z<b)=P(Z<b)−P(Z<a)
多个独立的正态分布
X
±
Y
,
方
差
均
为
+
X\pm Y,方差均为+
X±Y,方差均为+
X
∼
N
(
μ
x
,
σ
x
2
)
+
Y
∼
N
(
μ
y
,
σ
y
2
)
=
X
+
Y
∼
N
(
μ
x
+
μ
y
,
σ
x
2
+
σ
y
2
)
X \sim N(\mu_x,\sigma_x^2)+Y \sim N(\mu_y,\sigma_y^2)=X+Y \sim N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2)
X∼N(μx,σx2)+Y∼N(μy,σy2)=X+Y∼N(μx+μy,σx2+σy2)
X
∼
N
(
μ
x
,
σ
x
2
)
−
Y
∼
N
(
μ
y
,
σ
y
2
)
=
X
+
Y
∼
N
(
μ
x
+
μ
y
,
σ
x
2
+
σ
y
2
)
X \sim N(\mu_x,\sigma_x^2)-Y \sim N(\mu_y,\sigma_y^2)=X+Y \sim N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2)
X∼N(μx,σx2)−Y∼N(μy,σy2)=X+Y∼N(μx+μy,σx2+σy2)
E
(
X
±
Y
)
=
E
(
X
)
±
E
(
Y
)
,
存
疑
【
V
a
r
(
X
±
Y
)
=
V
a
r
(
X
)
±
V
a
r
(
Y
)
】
E(X\pm Y)=E(X)\pm E(Y),存疑【Var(X\pm Y)=Var(X)\pm Var(Y)】
E(X±Y)=E(X)±E(Y),存疑【Var(X±Y)=Var(X)±Var(Y)】
正太分布线性变换
a
X
+
b
∼
N
(
a
μ
+
b
,
a
2
σ
2
)
aX+b \sim N(a\mu+b,a^2\sigma^2)
aX+b∼N(aμ+b,a2σ2)
X 1 + X 2 + ⋯ + X n ∼ N ( n μ , n σ 2 ) X_1+X_2+\cdots+X_n \sim N(n\mu,n\sigma^2) X1+X2+⋯+Xn∼N(nμ,nσ2)
正太分布与二项分布( 当 n p 和 n q 均 大 于 5 时 , 可 用 正 态 分 布 近 似 替 代 二 项 分 布 当np和nq均大于5时,可用正态分布近似替代二项分布 当np和nq均大于5时,可用正态分布近似替代二项分布)
即:如果 X ∼ B ( n , p ) , 且 n p > 5 , n q > 5 , 则 可 以 使 用 X ∼ N ( n p , n p q ) X\sim B(n,p),且np>5,nq>5,则可以使用X\sim N(np,npq) X∼B(n,p),且np>5,nq>5,则可以使用X∼N(np,npq)仅是替代二项分布
注:进行替代时,需要进行连续性修正。(二项分布为离散型分布,正态分布是连续型分布)
-
计算 P ( X ≦ a ) P(X \leqq a) P(X≦a),正态分布修正为 P ( X < a + 0.5 ) P(X < a+0.5) P(X<a+0.5)
-
计算 P ( X ≧ b ) P(X \geqq b) P(X≧b),正态分布修正为 P ( X b + 0.5 ) P(X b+0.5) P(Xb+0.5)
-
计算 P ( a ≦ X ≦ b ) P(a\leqq X \leqq b) P(a≦X≦b),正态分布修正为 P ( a − 0.5 ≦ X ≦ b + 0.5 ) P(a-0.5\leqq X \leqq b+0.5) P(a−0.5≦X≦b+0.5)
正态分布与泊松分布 X ∼ P o ( λ ) ⇒ X ∼ N ( λ , λ ) X \sim Po(\lambda) \Rightarrow X \sim N(\lambda, \lambda) X∼Po(λ)⇒X∼N(λ,λ)。注:记得连续性修正
如何分析何时两者可替代。
看分布:看图。
-
当 λ \lambda λ很小时,泊松分布右偏,越小偏度越大。
-
当 λ \lambda λ很大时,泊松分布对称,接近正态分布。
★
\bigstar
★多大算很大?当
λ
>
15
时
\lambda>15时
λ>15时

抽样
-
总体:准备对其进行测量、研究或分析的整个群体。指客观存在的、在同一性质基础上结合起来的许多个别单位的整体。
-
样本:观测或调查的一部分个体,总体是研究对象的全部
-
样本调查:仅对总体的一个样本进行的研究或调查。
-
无偏样本:样本与总体样本具有相似的特性,该样本可代表目标样本
-
偏倚样本:样本与总体样本特性不相似,该样本无法代表目标样本。
偏倚来源:
-
抽样空间条目不齐
-
抽样单位不正确
-
为样本选取的一个个抽样单位未出现在实际样本中
-
调查问卷问题设计不当
-
样本缺乏随机性。
如何抽样:
-
确定目标总体,明确样本取自哪里
-
确定抽样单位,确定目标总体时所描述的对象类型。一粒口香糖,一盒口香糖。
-
确定抽样空间,一张列举目标总体范围内所有抽样单位,并且已经给每个抽样单位编好号的表。
抽样方法:
-
简单随机【不】[重复]抽样:抽签,随机编号生成等
-
分层抽样:将总体划分为几个组(层),组(层)中的单位都相似,每一组(层)都尽可能与其他组(层)不一样。分好组(层)以后,对每一层执行简单随机抽用哪个。
-
整群抽样:将总体划分为几个群,其中每个群都尽量与其他群像是,可通过随机抽样抽取几个群,然后用这些群中的每一个抽样单位形成样本。
-
系统抽样:选取一个数字k,抽取所有编号为k的整数倍的单位
样本估计
μ \mu μ:总体均值
X ˉ \bar{X} Xˉ:样本均值
μ ^ \hat{\mu} μ^:点估计量:由样本数据的得出,是总体参数的估计。
总体方差:
σ
2
=
∑
(
X
−
μ
)
2
n
\sigma^2=\frac{\sum(X-\mu)^2}{n}
σ2=n∑(X−μ)2
估计总体方差:
σ
2
^
=
∑
(
X
−
X
ˉ
)
2
n
−
1
\hat{\sigma^2}=\frac{\sum(X-\bar{X})^2}{n-1}
σ2^=n−1∑(X−Xˉ)2
比例的抽样分布–知道总体概率,计算样本概率
抽样分布:从一个总体用相同的方法抽取许多个大小相同但存在差异的样本,用每个样本的某个属性形成的一个分布,得到的结果成为抽样分布。可参考《中心极限定理》来理解。
如:现有一堆大包盒装糖球,每一盒装有100粒,红色糖球的总体概率为25%,求一大盒特定糖球中有40及以上颗红色糖球的概率。
糖球总体的25%为红球。在一盒装有100粒糖球的包装盒中,至少有40%红色糖球的概率有多大?
-
查看与特定样本大小相同的所有样本。此处n=100
如果有一个大小为n的样本,就需要考虑所有大小为n的可能样本
-
观察所有样本比例形成的分布,求出比例的期望和方差。
每一个样本都有自己的情况,因此每个包装盒的红色糖球的比例都有可能发生变化
-
得出上述比例的分布后,利用分布求概率。
得到一个样本的“成功比例”的分布后,就能够利用这个分布求出一个随机样本的比例概率,这里的随机样本是一大盒糖球。
X
∼
B
(
n
,
p
)
X\sim B(n,p)
X∼B(n,p)
P
s
=
X
/
n
P_s=X/n
Ps=X/n
其中n=100,p=0。



均值的抽样分布( X ˉ 的 分 布 \bar{X}的分布 Xˉ的分布)
若:一袋糖果数目均值为10,方差为1。
购买30袋糖球,均值小于等于8.5颗糖球的概率是多少。
-
查看研究样本大小相同的所有可能样本。此处n=30
如果有一个大小为n的样本,就需要考虑所有大小为n的可能样本
-
观察所有样本形成的分布,求出样本均值的期望和方差。
每一个样本都各有特点,每个包装袋中糖球数目有变化
-
得到样本均值分布后,用该分布求概率。
只要知道所有可能样本的均值的分布情况,就能利用该分部求出一个随机样本的均值的概率,在本例中,随机样本即小包装糖球。


3.均值标准差
均
值
标
准
误
差
=
σ
n
均值标准误差=\frac{\sigma}{\sqrt{n}}
均值标准误差=nσ
n越大,均值标准误差越小。也就是说,样本中的个体越多,作为总体均值的估计量的样本均值越可靠。

样本均值的抽样分布
中心极限定理:从均值为
μ
\mu
μ、方差为
σ
2
\sigma^2
σ2(有限)的总体中,抽取样本量为
n
n
n的随机样本,当
n
n
n充分大时(通常要求
n
≥
30
n ≥30
n≥30),样本均值的分布近似服从均值为
μ
\mu
μ ,方差为
σ
2
n
\frac{\sigma^2}{n}
nσ2 的正态分布。
X
ˉ
∼
N
(
μ
,
σ
2
n
)
\bar{X} \sim N(\mu, \frac{\sigma^2}{n})
Xˉ∼N(μ,nσ2)
若原分布为二项分布即
X
∼
B
(
n
,
p
)
X \sim B(n,p)
X∼B(n,p),则
X
ˉ
∼
N
(
n
p
,
p
q
)
\bar{X} \sim N(np, pq)
Xˉ∼N(np,pq)
若原分布为泊松分布即 X ∼ P o ( λ ) X \sim Po(\lambda) X∼Po(λ),则 X ˉ ∼ N ( λ , λ n ) \bar{X} \sim N(\lambda, \frac{\lambda}{n}) Xˉ∼N(λ,nλ)

置信区间
若 P ( a < μ < b ) = α P(a<\mu < b)= \alpha P(a<μ<b)=α则将(a,b)称为 α \alpha α的置信区间,基本默认a和b关于 μ \mu μ对称
如何求解置信区间
- 选择总体统计量
- 求出抽样分布
- 决定置信水平
- 求出置信上下限
因 P ( a < μ < b ) = α P(a<\mu < b)= \alpha P(a<μ<b)=α,则 P ( X ˉ < a ) = 1 2 α , 且 P ( X ˉ > b ) = 1 2 α P(\bar{X}<a)=\frac{1}{2}\alpha,且P(\bar{X}>b)=\frac{1}{2}\alpha P(Xˉ<a)=21α,且P(Xˉ>b)=21α
利用标准分,查表分别求得 a 和 b a和b a和b,此处 μ 和 σ 2 \mu和\sigma^2 μ和σ2已知或者能求。
置信区间简便算法:

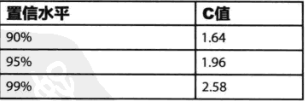

T分布
抽取一个样本,共10颗,得到样本的平均重量为0.5盎司,样本方差为0.09
如何求出总体的置信区间。
1.选择总体统计量
选取要为其构建置信区间的统计量。此处需要为糖球的重量均值搭建一个置信区间,也就是腰围总体均值μ构建置信区间。
由于需要求μ的置信区间,下一步则需要求均值的抽样分布。
2.求 X ˉ \bar{X} Xˉ的概率分布
此处不用正态分布的原因
当抽样很大时,正态分布是求置信区间的理想分布——能够得到精确结果,且与总体本身是否是正太分布无关
1.不知道总体方差,因此无法利用样本数估计σ²,虽然我们可以通过点估计完成,但是
2.样本太小。
当样本量很小时,
X
ˉ
符
合
t
分
布
\bar{X}符合t分布
Xˉ符合t分布
T
∼
t
(
v
)
T \sim t(v)
T∼t(v)
v
v
v为自由度,
v
=
n
−
1
v=n-1
v=n−1,
n
n
n为样本的大小
求
t
t
t分布的标准分
T
=
X
ˉ
−
μ
s
n
T=\frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}}
T=nsXˉ−μ
类似标准分
Z
Z
Z,不过此处方差为
σ
2
n
\frac{\sigma^2}{n}
nσ2,标准差为
σ
n
\frac{\sigma}{\sqrt{n}}
nσ,并且用
s
s
s代替
σ
\sigma
σ而已

3.决定置信水平
置信水平:希望对“置信区间包含总统计量”的可信程度
置信水平:如果研究人员按照有效方法重复计算测算 95% 置信区间,那么平均来说,其中 95% 将包含 (或覆盖) 真实效应大小。因此,上述置信水平被称作覆盖概率 (coverage probability) 。
显著性水平
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率,用α表示。
显著性水平代表的意义是在一次试验中小概率事物发生的可能性大小。
假设检验运用了小概率原理,事先确定的作为判断的界限,即允许的小概率的标准,称为显著性水平。
4.求出置信上下限
(
x
ˉ
−
t
s
n
,
x
ˉ
+
t
s
n
)
(\bar{x}-t\frac{s}{\sqrt{n}},\bar{x}+t\frac{s}{\sqrt{n}})
(xˉ−tns,xˉ+tns)
其中
P
(
−
t
≤
T
≤
t
)
=
α
(
此
处
α
=
0.95
)
P(-t \le T \le t)=\alpha (此处\alpha=0.95)
P(−t≤T≤t)=α(此处α=0.95)
查表,
v
=
n
−
1
(
自
由
度
,
此
处
等
于
7
)
,
p
=
1
−
α
2
(
此
处
等
于
0.025
)
v=n-1(自由度,此处等于7),p=\frac{1-\alpha}{2}(此处等于0.025)
v=n−1(自由度,此处等于7),p=21−α(此处等于0.025)



假设检验
假设检验(hypothesis testing),又称统计假设检验,是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。
制药公司断言自己的要能在两周内治愈90%的患者。
当下抽样15人,结果显示
是否治愈 是 否
频数 11 4
- 查看断言
记下制药公司的断言
- 查看证据
看看我们需要哪些证据才可以否定制药公司的断言,并把所需要的证据和我们手头现有的证据进行比较。方法是:先假设制药公司的断言属实,然后看看医生得到的结论是否有误。
- 做出决策
根据证据,接受或否定制药公司的断言。
假设检验的六个步骤
-
确定进行检验的假设:即我们要对其进行试验的断言
该断言也成为假设。 根据制药公司的断言,药物能在两周内治愈90%的患者。除非有充分证据进行反驳,否则就要接受这个结论。 把这个断言称为原假设,H0表示。除非有充分证据进行反驳,否则就要接受这个断言。 此处:H0:p=90% 与原假设对立的断言称为备择假设,用H1表示。如果有足够证据拒接H0,我们就接受H1. 此处H1:p<90%进行假设检验时,你假定原假设为真;如果有足够的证据反驳原假设,则拒绝原假设,接受备择假设
-
选择检验统计量:我们需要选取能最有效地对断言进行检验的统计量
“检验统计量”用于对假设进行检验的统计量,是与该检验关系最为密切的统计量。如果用X表示样本人数,就可以将X作为检验统计量。样本中公有15名患者,根据制药公司的说法,成功概率为0.9.由于X符合二项分布,于是检验统计量实际上符合:
X ∼ B ( 15 , 0.9 ) X \sim B(15,0.9) X∼B(15,0.9)
为什么成功概率是0.9?我们需要检验时否有充足的证据反驳原假设。 办法是:首先假设H0为真,然后寻找不利于H0的证据。 在针对制药事件中,我们假设治愈的概率为0.9——除非有有力的证据证明这不成立。 为此,我们假定治愈的概率为0.9,看看得出观察结果的可能性有多大。 也就是说,取样本结果,然后甲酸发生这个结果的概率——我们通过求拒绝域实现这个目标。 -
确定用于做决策的拒绝域:我们需要使用某种确定性水平
假设检验的决绝与是一组数值,这组数值给出反驳原假设的最极端证据。 如果之于人数为90%或者90%以上,这就与制药公司的断言吻合。随着治愈人数下降,制药公司的断言为真的可能性越来越小。 我们需要通过某种方法支出何时能够合理地拒绝原假设——指定一个拒绝域即可实现这一目的。如果患者的之于人数位于拒绝域以内,我们就说有足够的证据反驳原假设;如果之于人数位于拒绝域以外,我们就承认没有足够的证据可以反驳原假设,并接受制药公司的断言。 我们把拒绝域的分界点称为“C”——临界值。 检验的显著性水平所量度的是一种愿望,即:希望在样本结果的不可能程度达到多大时,就拒绝原假设H0,。像置信区间的置信水平一样,显著性水平以百分数表示。 例如,假设我们想要以5%为显著水平检验制药公司的断言,这说明我们选取的拒绝域应使得“患者治愈人数小于c”的概率小于0.05,即概率分布最低端的5%部分。即我们的拒绝域定义为能令下列不等式成立的一些数值:
P ( X < c ) < α 其 中 α = 5 P(X<c) < \alpha \\ 其中\alpha=5% P(X<c)<α其中α=5构建拒绝域时,有单尾检验和双尾检验的区别。 选择一个α显著性水平 单尾检验 < 拒绝域(0,α), 非拒绝域(α,100%) > 拒绝域(0,100%-α), 非拒绝域(100%-α,100%) 双尾检验 拒绝域(0,α/2),(100-α/2,100), 非拒绝域(α/2,100%-α/2) -
求出检验统计量的p值:我们需要了解在假定断言为真的情况下,我们的实验结果的可信程度
P值:即某个小于或者等于拒绝域方向上的一个样本数值的概率 具体求法是利用样本进行计算,然后判定样本结果是否落在假设检验的拒绝域以内。

-
查看样本结果是否谓语拒绝域内:接着需要了解试验结果是否位于确定性限值范围中。
4可知P=0.0555,由于P>α,即样本中治愈的患者数不在拒绝域内。 拒绝域:(0,5%) 接受域:(5%,100%) -
做出决策
因为假设检验P值落在了检验的拒绝域以外,因此,我们没有充分的证据可以拒绝原假设。 所以,我们接受制药公司的断言。断言

- 第一类错误:错误地拒绝真原假设。弃真错误
- 第二类错误:错误地接受假原假设。取伪错误
| 接受 H 0 H_0 H0 | 拒绝 H 0 H_0 H0 | |
|---|---|---|
| H 0 H_0 H0真 | √ \surd √ | 第一类错误 |
| H 0 H_0 H0假 | 第二类错误 | √ \surd √ |
P ( 第 一 类 错 误 ) = α P(第一类错误)=\alpha P(第一类错误)=α
P ( 第 二 类 错 误 ) = β P(第二类错误)=\beta P(第二类错误)=β
如何求 β \beta β
- 检查是否拥有 H 1 H_1 H1的特定数值。没有这个数值则无法计算第二类错误的概率
- 求检验拒绝域以外的数值范围。如果检验统计量已经标准化,则该数值范围要进行逆标准化。
- 假定 H 1 H_1 H1为真,求得到这些数值的概率。也就是说,我们要求出得到拒绝域以外的数值的概率,但这一次用 H 1 H_1 H1而不是 H 0 H_0 H0对检验统计量进行描述。
功效
只要求出 P ( 第 二 类 错 误 ) P(第二类错误) P(第二类错误),再计算假设检验的功效容易了
在
H
0
H_0
H0为假时拒绝
H
0
H_0
H0其实就是发生第二类错误的相反情况。即
功
效
=
1
−
β
功效=1-\beta
功效=1−β


X
2
X^2
X2分布
-
卡方分布:通过一个检验统计量来比较期望结果和实际结果之间的差别,然后得出观察频数机极值的发生概率。
-
卡方检验:统计样本的实际观测值与理论推断值之间的偏离程度
★ \bigstar ★ χ 2 \chi^2 χ2概率分布主要用于检查实际结果与预期结果之间合适存在显著差别。
检验统计量
χ
2
\chi^2
χ2的计算方法:
χ
2
=
∑
(
O
−
E
)
2
E
\chi^2 = \sum\frac{(O-E)^2}{E}
χ2=∑E(O−E)2
其中E代表期望频数,O为观察频数。
即,对于概率分布中的每一个概率,取期望频数和实际频数的差的平方数,再除以期望频数,然后加总。
卡方检验作用:
- 检验拟合优度:检验一组给定的数据与指定分布的吻合程度。
- 检验两个变量的独立性:检验变量之间是否存在某种关联。
χ
2
\chi^2
χ2分布用到一个参数——希腊字母ν,读作“纽”
X
2
∼
χ
2
(
ν
)
X^2 \sim \chi^2(\nu)
X2∼χ2(ν)
ν
\nu
ν表示自由度
ν
=
(
组
数
)
[
行
数
]
−
(
限
制
数
)
\nu=(组数)[行数]-(限制数)
ν=(组数)[行数]−(限制数)

χ
α
2
(
ν
)
\chi^2_\alpha(\nu)
χα2(ν)
查表:
α
\alpha
α对应列,
ν
\nu
ν对应行
χ 2 \chi^2 χ2假设检验-步骤
- 确定要进行检验的假设及其备择假设
- 求出期望频数和自由度
- 确定用于做决策的拒绝域
- 计算检验统计量 χ 2 \chi^2 χ2
- 查看检验统计量是否谓语拒绝域以内
- 作出决策




独立性
χ
2
\chi^2
χ2检验可用于判断两种因素是否相互独立,或两者是否看上去互有联系
检验过程:设立一个假设,用观察频数和期望频数计算
χ
2
\chi^2
χ2检验统计量,然后查看结果是否落在拒绝域以内。


自
由
度
ν
=
(
h
−
1
)
×
(
k
−
1
)
自由度\nu = (h-1) \times (k-1)
自由度ν=(h−1)×(k−1)



相关与回归

-
其
中
σ
x
与
v
a
r
(
x
)
均
为
标
准
差
,
写
法
不
同
而
已
其中\sigma_x与var(x)均为标准差,写法不同而已
其中σx与var(x)均为标准差,写法不同而已



























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








