BST树(Binary Search Tree)二叉搜索树

 BST树为典型的数据结构，广泛应用于数据群的管理上，如C++中的set/map集合就运用到了二叉搜索树的结构特点，BST树是一种动态查找树，在查找的过程中可以自动“生长”，且新增的数据永远在树的最下层上，为叶子节点。

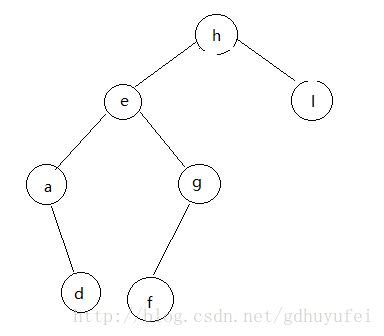
二叉搜索树它的左右子树也为二叉搜索树，不管其名称如何，但结构是树的特点就具备了递归的定义。二叉搜索树中结点的值总是大于左子树且小于右子树的值，如图：

                                                                                              

h的左子树的值均小于h,右子树的值均大于h,对于e为根节点，其原理也是一样,因为二叉树是具备递归性质的。如果把这个BST树对其中序遍历，就会得到序列：adefghl,发现到中序遍历BST树就得到一个非递减的有序序列，其实构造一颗BST树的过程就是对输入数据进行排序的过程。

构造一颗BST树就用到了BST树的定义，其数据结构用的就是用来表示二叉树的二叉链表存储结构:

typedef struct BTNode{
	char data;
	struct BTNode*left;
	struct BTNode*right;
}*BiTree;

数据用data域存储，left和right指针指向左右孩子.

建立一颗二叉树的过程(先序递归建立):

void CreateBiTree(BiTree&T){
	char ch;
	scanf_s("%c", &ch);
	if (ch == '_'){//如果输入是'_'表示无左孩子或者是右孩子
		T = NULL;//对应的指向孩子的指针为空
	}
	else {
		if ((T = (BiTree)malloc(sizeof(BTNode))) == NULL){
			printf("分配节点失败\n");
			exit(EXIT_FAILURE);
		}
		T->data = ch;
		CreateBiTree(T->left);
		CreateBiTree(T->right);
	}
}

已上图所示的二叉树为例，输入为:hea_d__gf___l__

用先序和中序遍历次二叉树可得：

void PreOrderTraverse(BiTree&T){
	if (T){
		printf("%c ", T->data);
		PreOrderTraverse(T->left);
		PreOrderTraverse(T->right);
	}
}
void InOrderTraverse(BiTree&T){
	if (T){
		InOrderTraverse(T->left);
		printf("%c ", T->data);
		InOrderTraverse(T->right);
	}
}

检验先序和中序遍历可得到唯一的二叉树就是上图所示的二叉树。

接下来就是构造二叉排序树。

首先是BST树的查找：它首先从根节点出发，如果待查找值小于根节点则在左子树中查找，否则在右子树查找。如此递归。

/*
	在二叉搜索树T中查找数据等于data的结点，若找到p指向该结点
	返回1否则p指向查找路径上,访问的最后一个结点，返回0，f指向T的双亲结点,f的初值为NULL
*/
int SearchBST(BiTree&T, char data, BiTree f, BiTree&p){
	if (!T){
		p = f;
		return 0;
	}
	if (T->data == data){
		p = T;
		return 1;
	}
	else if (data < T->data){
		return SearchBST(T->left, data, T, p);
	}
	else{
		return SearchBST(T->right, data, T, p);
	}
}

查找到了则返回指向这个节点的指针，如果找不到就传出参数p指针指向查找路径上访问的最后一个结点，接下俩要插入的新节点不是p指向的左孩子就是右孩子。所以下不操作就是插入BST树的算法：

/*
	在二叉搜索树中插入一个值为data的结点,成功返回1，若失败则存在该结点返回0
*/
int InsertBST(BiTree&T, char data){
	BiTree p, s;
	if (!SearchBST(T, data, NULL, p)){//没有找到值为data的结点,此时p指向查找路径上访问的最后一个结点
		if ((s = (BiTree)malloc(sizeof(BTNode))) == NULL){
			printf("分配节点失败");
			exit(EXIT_FAILURE);
		}
		s->data = data;
		s->left = s->right = NULL;//新节点的左右孩子均为空,因为在二叉搜索树中新插入的结点一定是叶子节点

		if (!p){//树T为空则新结点为根节点
			T = s;
		}
		else if (data < p->data){//判断新节点插入在哪个位置
			p->left = s;
		}
		else{
			p->right = s;
		}
		return 1;
	}
	else
		return 0;
}

如此一来一颗BST树就构造好了，当然可以按照二叉树建立的方式构造，也可以按照BST树的定义构造。但插入结点的操作都是一样的。

那么，如何在BST树中删除一个节点呢？

分为两种大情况：

一、

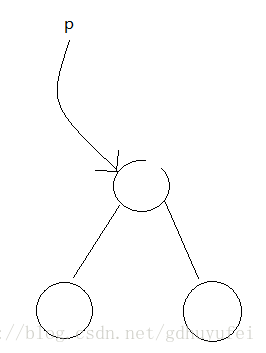
     待删结点至多有一颗子树待删结点有一颗左子树，如图：

                        

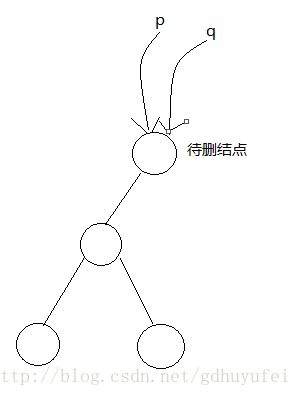
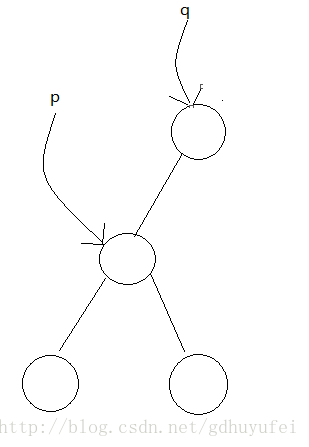
                                  ①                                                            ②                                                           ③

同样待删结点的右子树和上图同一个道理：

 二、

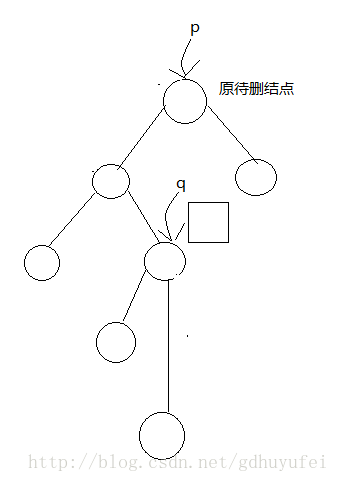
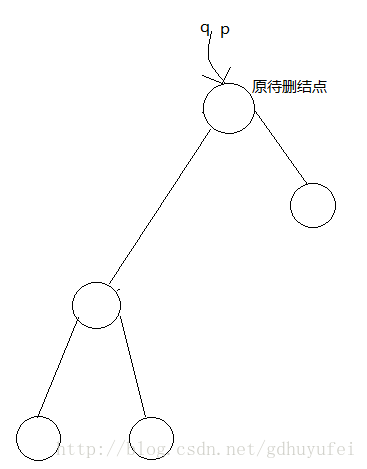
          待删结点有左右子树，此时删掉结点不是真正的删掉了，而是将待删结点的前驱结点值赋给待删结点的值，而删除这个前驱结点。这样逻辑上可以实现删掉了结点，但结构上并没有真正删除，因为删除一颗二叉树的非叶子节点会破坏这个作为根节点的非叶子结点的子树的结构。找到待删结点到底前驱结点和简单，只需总待删结点的左子树开始一直往右寻找到最右结点，直到结束，这个结点就为待删结点的前驱结点。

如图：

                                    

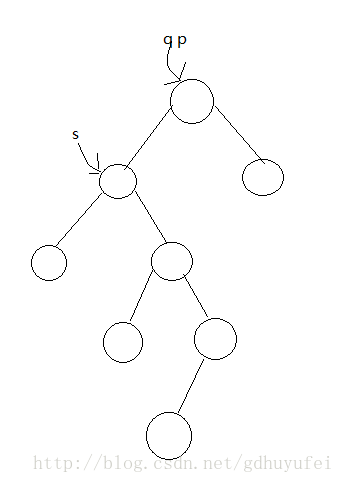
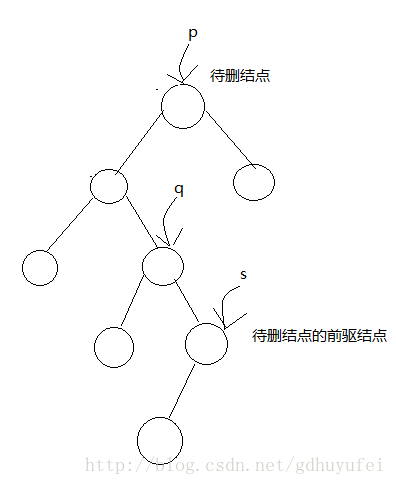
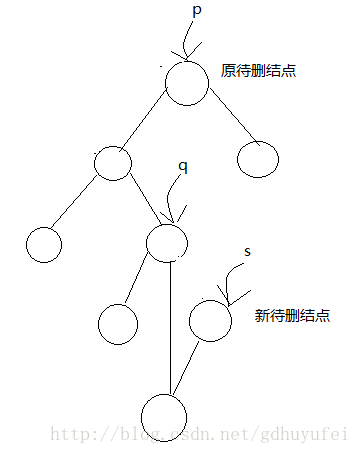
这是待删结点的左孩子有右子树的情况，下图为待删结点的左子树无右子树的情况：

                                                                                    

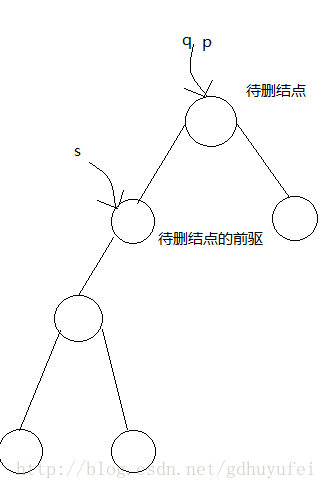
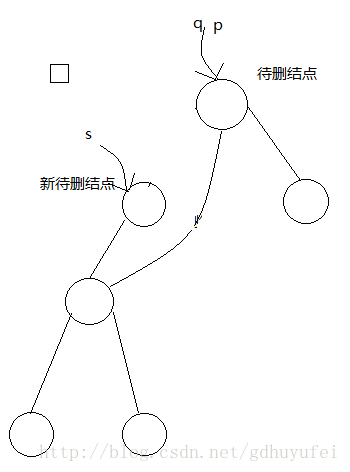
、源码如下：

void Delete(BiTree&p){
	BiTree s, q;
	q = p;
	if (!p->right){//p没有右孩子
		p = p->left;
		free(q);
	}
	else if (!p->left){
		p = p->right;
		free(q);
	}
	else{//p有左右子树
		s = p->left;//s左转,准备找到p的左子树的最右结点
		while (s->right){
			q = s;
			s = s->right;
		}
		//查找结束后s指向p的左子树的最右结点,q为s的双亲结点
		p->data = s->data;
		if (q != p){//p的左子树有右孩子
			q->right = s->left;//s一定没有右孩子否则s就指向s的右孩子了
		}
		else{//p的左子树没有右孩子
			q->left = s->left;
		}
		free(s);
	}
	
}

int DeleteBST(BiTree&T, char data){
	if (!T){
		return -1;
	}
	if (data == T->data){
		Delete(T);
	}
	else if (data < T->data){
		Delete(T->left);
	}
	else{
		Delete(T->right);
	}
	return 1;
}