http://blog.csdn.net/luckyxiaoqiang/article/details/8788906
1,rand7()构造rand10()
只调用一次rand7()肯定无法达到目的。我们调用两次rand7(),这样我们可以随机的得到1~49中的一个数,为什么呢?
我们将49分成7段,1~7,8~14,15~21,22~28,29~35,36~42,43~49,第一次rand7()随机选择其中一段,第二次rand7(),随机选择段内的一个数,这样我们得到的1~49中的数都是等概率的。即”(rand7()-1)*7+rand7()“。然后我们想办法将1~49映射到1~10,显然无法直接映射,我们只取1~40,对于41~49我们抛弃,这样并没有影响其随机特性,因为1~40中的每一个数都是等概率出现的。
然后(1~4)→1,(5~8)→2,……。这样就完成了rand10的功能。
int rand10()
{
int x;
do
{
x = (rand7()-1)*7+rand7();
}while(x > 40)
return x%10+1;
}2,利用randA()构造硬币概率
问题:有一个随机生成器randA(),以p的概率返回0,1-p的概率返回1,利用这个randA()构造randB(),使randB()等概率的返回0和1,即0.5的概率返回0,0.5的概率返回1。
只调用一次randA(),我们也无法实现randB(),所以也要调用两次。调用两次共有4种结果,得到00,概率为p*p;得到01,概率为p*(1-p);得到10,概率为(1-p)*p;得到11,概率为(1-p)*(1-p)。容易发现有两种情形概率相等,01和10,那么我们可以把这两种情况映射为返回0或1,如果得到的是其它两种情况,那么我们就继续再调用两次randA();
int randB()
{
int x1, x2;
do
{
x1 = randA();
x2 = randA();
}while(x1+x2 != 1)
return x1;
}3,随机shuffle
问题:给出一个n个元素的数组,对所有元素随机中排,也就是说,n!种可能的元素排列中随机选出一种。
void random_shuffle(int A[], int n)
{
for(int i = n-1; i > 0; i--)
{
swap(a[i], a[Rand(0, i)]);//即随机选择0~i中的一个元素
}
}简单验证一下,详细证明请参考Knuth的《计算机程序设计艺术 第2卷 半数值算法》。
当对于第n-1个位置,swap(a[n-1], a[Rand(0, n-1)]),使得每一个元素出现在位置n-1的概率都是1/n;
再考虑第n-2个位置,每个元素出现在第n-2个位置上的概率是(n-1)/n * 1/(n-1) = 1/n,即在第n-1个位置没有被选中,然后在第n-2个位置被选中;
再考虑第n-3个位置,每个元素出现在第n-3个位置上的概率是(n-1)/n * (n-2)/(n-1) * 1/(n-2) = 1/n,在第n-1和第n-2个位置都没有被选中,然后在第n-3个位置被选中。
。。。
4,产生无重复随机数序列
问题:程序的输入包含两个整数m和n,其中m<n。输出是0~n-1范围内m个随机整数的有序列表,不允许重复。从概率的角度来说,我们希望得到没有重复的选择,其中每个选择出现的概率相等。
void generate(int m,int n)
{
int t = m;
for(int i = 0; i < n; i++)
if(Rand(0,n-1-i) < t) //即以t/(n-i)的概率执行下面的语句
{
printf("%d\n",i);
t--;
}
}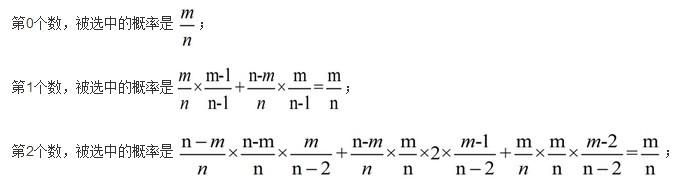






















 3797
3797

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








