Floyd - Warshall 算法

算法只有五句代码，来计算任意两个城市间最短路径

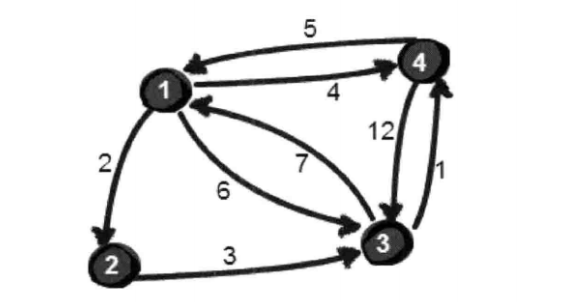
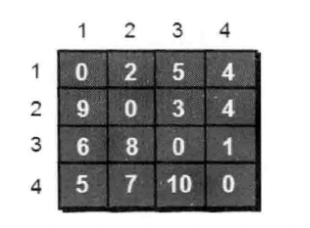
4个城市 8条线路 ，用图来表示相邻城市的距离

代码为：
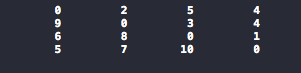
a[1][1]=0 代表从城市1 到城市1 不动，距离为0
a[1][2]=2 代表城市1到城市2距离为2
a[2][1]=inf 代表城市2 不能直接回到城市1 距离无限大

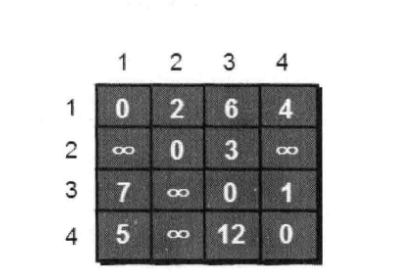
4->3 = 12
4->1->3=5+6=11<12
因此引入第三个点的时候—–有可能使得两点间的距离变短，
因此，按顺序引入1.让两点间一定要经过1，如果发现比原先的数值小，就进行替换
a[4][3]由12 变成了11
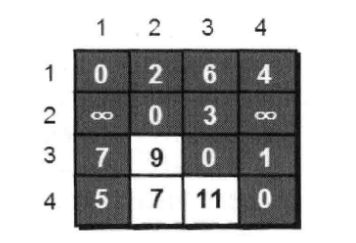
同理a[3][2]=a[3][1]+a[1][2]=7+2=9<%%
a[4][2]=a[4][1]+a[1][2]=5+2=7<%%

现在就把最小值进行变更，

到目前为止所有点如果经过点1 会变小总路径的都考虑进去了。。。

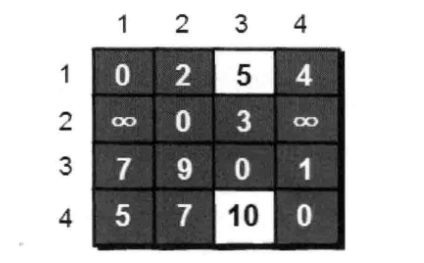
接下来就考虑需要经过点1 也要经过点2————-就在新的图继续找

a[1][3]= a[1][2]+a[2][3]=2+3=5<6
a[4][3]= a[4][2]+a[2][3]=7+3=10<11

类推—-经过了1—2—-3—-4 每次发现经过第三个点的的路径比原来两点间的距离小，
就进行替换操作—–写成代码：

- (void)main{
    int e[10][10],k,i,j,n,m;
    int inf = 99999999;//用inf存储一个我们认为的正无穷值
    //读入n和m，n表示顶点个数，m表示边的条数
    n=4;m=8;

    for (i=1; i<=n; i++)
        for (j=1; j<=n; j++)
            if (i==j) e[i][j]=0;
               else     e[i][j]= inf;

    e[1][2]=2;
    e[1][3]=6;
    e[1][4]=4;
    e[2][3]=3;
    e[3][1]=7;
    e[3][4]=1;
    e[4][1]=5;
    e[4][3]=12;


    //Floyd - Warshall 算法核心语句
    //核心思想：从i号顶点到j号顶点只经过前k号点的最短路径 ,代表按顺序经过
    //k=1，=2，=3=4的路径，遇到小的就替换原来的数值。。。。。。e[i][j]代表所在点的数值
    for (k=1; k<=n; k++)

        for (i=1; i<=n;i++ )
            for (j=1; j<=n; j++)

                if (e[i][j]>e[i][k] + e[k][j])
                    e[i][j] = e[i][k]+e[k][j];

    for (i=1; i<=n; i++) {
        for (j=1; j<=n; j++) {
            printf("%10d",e[i][j]);
        }
        printf("\n");
    }

}

显示的结果

画图显示就是

时间复杂度为N*N*N