常用的查找算法简介以及AVL树

最新推荐文章于 2022-11-13 17:32:42 发布

长不大的大灰狼

最新推荐文章于 2022-11-13 17:32:42 发布

阅读量1.4k

点赞数

分类专栏：数据结构进阶文章标签：数据结构二叉树 java

本文链接：https://blog.csdn.net/glpghz/article/details/107167623

版权

数据结构进阶专栏收录该内容

5 篇文章 1 订阅

订阅专栏

平衡二叉搜索树——AVL树

——平衡二叉搜索树（Self-balancing binary search tree）

Ⅰ 搜索/查找——相关的算法及数据结构

（1）遍历查找

比较方式：equals()
时间复杂度：O(n)

public static int Search(int[] a, int key) {
	for (int i = 0; i < a.length; i++) {
		if (a[i] == key)
			return i;
	}
	return -1;
}

（2）二分查找

比较方式：compare()
时间复杂度：O(log n)

对数据要求强约束：

必须是数组（采用顺序存储）
数据必须有序

二分查找是基于比较的查找（小于中间值的往左边找，大于中间值的往右边找），只适合于静态数据（数据不会发生变化），因为插入或者删除可能会破坏数组的有序性，而为了维护约束往往需要付出O(n)的时间复杂度。


public static int binarySearch(int[] a, int key) {
	int low, mid, high;
	low = 0;// 最小下标
	high = a.length - 1;// 最大小标
	while (low <= high) {
		mid = (high + low) / 2;// 中间下标
		if (key > a[mid]) {
			low = mid + 1; // 关键字比中间值大
		} else if (key < a[mid]) {
			high = mid - 1;// 关键字比中间值小
		} else {
			return mid; // 当 key == a[mid] 返回目标值
		}
	}
	return -1;
}

（3）适合动态数据的查找算法（能够很好的支持insert/update/delete）

1）哈希表

HashMap/HashSet
比较方式：equals()
时间复杂度：O(1)

2）搜索树（平衡搜索树）

TreeMap/TreeSet
比较方式：compare()
时间复杂度：O(log n)

3）分组查找（Redis的跳表可以看作是这种结构的变形）

在这里插入图片描述
要求A<B<C，查找时可以很快找到在哪个组中查找，组内部的数据维护的比较松散（通过牺牲一定的查找性能，换来增删改性能的提升。）

Ⅱ 二叉搜索树

二叉搜索树又称二叉排序树，它是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

二叉搜索树具有以下特性：

二叉搜索树中最左侧的节点是树中最小的节点，最右侧节点一定是树中最大的节点
采用中序遍历遍历二叉搜索树，可以得到一个有序的序列

二叉搜索树最主要的作用是进行查询，插入和删除操作，也都是建立在查找的基础之上的。
在这里插入图片描述
总能在node==null的位置找到插入位置。

二叉树查询性能分析
插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
在这里插入图片描述
最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：O(log(n))
最差情况下，二叉搜索树退化为单支树，其平均比较次数为：O(n)
如果退化成单支树，二叉搜索树的性能就失去了，所以需要对其进行改进。

Ⅲ AVL树——平衡二叉搜索树

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序，二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

一棵AVL树是空树，或者是具有以下性质的二叉搜索树：

它的左右子树都是AVL树，左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在O(log n)，搜索时间复杂度O(log n)。

(1) AVL树性能分析

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即O(log(n))。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

(2) AVL树节点的定义

为了AVL树实现简单，AVL树节点在定义时维护一个平衡因子，具体节点定义如下：

class AVLTreeNode
{
   public AVLTreeNode(int val)
  {
       this.val = val;
  }
   public AVLTreeNode left = null;    // 节点的左孩子
   public AVLTreeNode right = null;   // 节点的右孩子
   public AVLTreeNode parent = null;  // 节点的双亲
   public int val = 0;
   public int bf = 0;   // 当前节点的平衡因子
}

平衡因子：BF(node) = H(node.left) - H(node.right)

(3) AVL树的查找：

和普通搜索树的查找方式相同。

(4) AVL树的插入:

插入之前：整棵树满足AVL的特征
插入期间：AVL的特征可能会被破坏掉，所以在插入过程中需要修复AVL树的特征
插入之后：整棵树满足AVL的特征

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步：

1). 按照二叉搜索树的方式插入新节点

在这里插入图片描述

2). 调整节点的平衡因子

在这里插入图片描述

更新后我们需要考虑两个点：

parent的BF值是否破坏了AVL树的特征
parent树的高度H(parent)是否发生了变化

情况一： 插入后BF=0，AVL特征没有被破坏，所以本次插入结束。

情况二： 插入后BF=1或-1，BF满足AVL，但是H(parent)的高度发生了变化，所以调节过程要向根的方向蔓延。
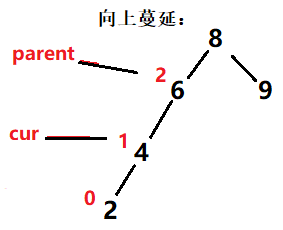
在这里插入图片描述
情况三： BF=2或-2，BF(parent)不满足AVL树，发生了失衡（在首次调节的过程中，或蔓延的过程中发生了失衡）。

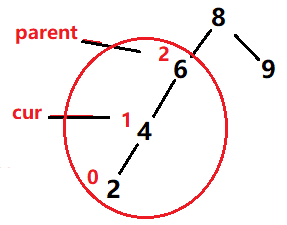
此时需要对红色范围内的节点进行调整，使树满足AVL，高度变为原来的高度。

AVL树的旋转（情况三）
如果在一棵原本是平衡的AVL树中插入一个新节点，造成了不平衡，此时必须调整树的结构，使之平衡化。根据节点插入位置的不同，AVL树的旋转分为四种：

1）左左（插入点.parent在失衡点的左边，插入点在parent的左边）：右旋
在这里插入图片描述
2）左右（插入点.parent在失衡点的左边，插入点在parent的右边）：先左旋再右旋

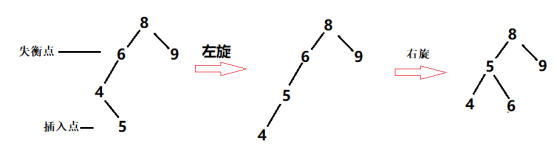
3) 右右（插入点.parent在失衡点的右边，插入点在parent的右边）：左旋

4) 右左（插入点.parent在失衡点的右边，插入点在parent的左边）：先右旋再左旋
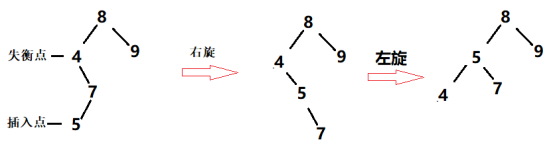
在这里插入图片描述

3) 失衡修复后平衡因子的计算

左左失衡：
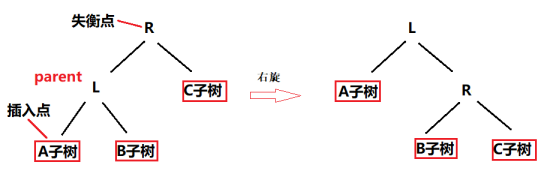
在这里插入图片描述
假设A子树是插入点，R节点是失衡点，
左左失衡BF®=2，即H(L)-H(C) =2;设H(C) = x; 则H(L) = x+2;
因为（H(L) = max(H(A),H(B))+1），那么A子树和B子树一定有一颗树的高度为x+1; 如果B子树的高度为x+1，那么L树在A子树插入前就是x+2了，所以不成立。

推出H(A)=x+1; H(B)=x, 因为若H(B)=x-1，那么失衡点就是L了，而不会是R了。
在这里插入图片描述
推出A,B,C子树的高度，即可得到失衡点和parent的BF了，即BF(R)=0; BF(L)=0。

左右失衡：
要求得各个节点的BF是多少，知道A,B,C,D四颗子树的高度即可。
在这里插入图片描述
左右失衡，BF(R) = 2;
设H(D) =x;则H(L) = x+2
因为（H(L) = max(H(A),H(P))+1），那么A子树和B子树一定有一颗树的高度为x+1;
如果A子树的高度为x+1，那么L树在P子树插入前就是x+2了，所以不成立。推出H(P)=x+1;
H(A)=x。因为若H(A)=x-1，那么失衡点就是L了，而不会是R了。
1)如果插入点来自B子树，H(B)=x, H(C) = x-1;
2)如果插入点来自C子树，H(C)=x, H(B) = x-1;
3)如果插入点来自P子树，H(C)=0, H(B) = 0;x=0;

BF(P)==1,插入点来自B子树，H(B)=x, H(C) = x-1; 此时H(A,B,D)=X, H(C)=x-1，则H(L)=x+1, H(R) = x+1,
推出：BF(L) =0, BF(R)=-1, BF(P) = 0;
BF(P)==-1,插入点来自C子树，H(C)=x, H(B) = x-1;此时H(A,C,D)=X, H(B)=x-1，则H(L)=x+1, H(R) = x+1,
推出：BF(L) =1, BF(R)=0, BF(P) = 0;
BF(P)==0,插入点就是P子树，H(C)=0, H(B) = 0;此时H(A,B,C,D)=0,则H(L)=1, H(R) =1,
推出：BF(L) =0, BF(R)=0, BF(P) = 0;

右左失衡：
在这里插入图片描述
右左失衡，BF(R) = -2;
设H(A) =x; H(A)-H(L)=-2;则H(L) = 2+x
因为（H(L) = max(H(D),H(P))+1），那么P子树和D子树一定有一颗树的高度为x+1;
如果D子树的高度为x+1，那么L树在P子树插入前就是x+2了，所以不成立。推出H(P)=x+1;
H(D)=x。因为若H(D)=x-1，那么失衡点就是L了，而不会是R了。
1)如果插入点来自B子树，H(B)=x,H(C) =x-1;
2)如果插入点来自C子树，H(C)=x,H(B) = x-1;
3)如果插入点来自P子树，则H(C)=0,H(B) = 0; x=0;

BF(P)==1,插入点来自B子树，H(B)=x, H(C) =x-1;此时H(A,B,D)=x, H(C)=x-1，则H(L)=x+1, H(R) = x+1,
推出：BF(L) =-1, BF(R)=0, BF(P) = 0;
BF(P)==-1,插入点来自C子树，H(C)=x,H(B) = x-1;此时H(A,C,D)=x,H(B)=x-1，则H(L)=x+1, H(R) = x+1
推出：BF(L) =1, BF(R)=0, BF(P) = 0;
BF(P)==0,插入点就是P子树，H(C)=0,H(B) = 0;此时H(A,B,C,D)=0,则H(L)=1, H(R) =1,
推出：BF(L) =0, BF(R)=0, BF(P) = 0;

(5) 调整为AVL树（举例）

在这里插入图片描述

Ⅳ 插入过程整理：

按照普通搜索树的方式进行插入，插入后需要调整平衡因子:
需要调整BF的节点为parent,如果插入点来自parent.left,则BF(parent)++;如果插入点来自parent.right,则BF(parent)--.

针对BF调整之后的结果，进行相应的处理：
在这里插入图片描述
（1）处理失衡的情况：

左左失衡，对右旋
左右失衡，先左旋后右旋
右右失衡，左旋
右左失衡，先右旋后左旋

（2）更新旋转后的BF:
1）左左失衡: BF(失衡点) = BF(失衡点.left) = 0

2）右右失衡：BF(失衡点) = BF(失衡点.right) = 0

3）左右失衡（分情况讨论）：

如果原BF(失衡点.left.right)==1，推出：BF(失衡点.left) =0, BF(失衡点)=-1, BF(失衡点.left.right) = 0;
如果原BF(失衡点.left.right)==-1，推出：BF(失衡点.left) =1, BF(失衡点)=0, BF(失衡点.left.right) = 0;
如果原BF(失衡点.left.right)==0，推出：BF(失衡点.left) =0, BF(失衡点)=0, BF(失衡点.left.right) = 0;

4）右左失衡（分情况讨论）：

如果原BF(失衡点.right.left)==1，推出：BF(失衡点.right) =-1, BF(失衡点)=0, BF(失衡点.right.left) = 0;
如果原BF(失衡点.right.left)==-1，推出：BF(失衡点.right) =1, BF(失衡点)=0, BF(失衡点.right.left) = 0;
如果原BF(失衡点.right.left)==0，推出：BF(失衡点.right) =0, BF(失衡点)=0, BF(失衡点.right.left) = 0;

Ⅴ AVL树实现:

（1）Node.java

public class Node {
    int key;

    /**
     * 平衡因子
     */
    int bf;

    Node left;
    Node right;

    /**
     * 记录结点的父结点，如果结点是根结点，则 parent == null
     */
    Node parent;

    Node(int key, Node parent) {
        this.key = key;
        this.bf = 0;
        this.left = null;
        this.right = null;
        this.parent = parent;
    }
}

（2）AVLTree.java

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

// 实现 纯 key 模型的 AVL 树
// 如果要实现 key-value 模型，只需要在结点中，多保存一个 value 即可
public class AVLTree {
    /**
     * 记录树的根结点，如果是空树，则 root == null
     */
    private Node root = null;

    /**
     * 插入 AVL 树
     * @param key 要插入的关键字
     * @throws RuntimeException 如果 key 重复了
     */
    public void insert(int key) {
        if (root == null) {
            // 空树的插入，单独处理即可
            root = new Node(key, null);
            return;
        }

        // 走到这里，肯定不是空树
        Node parent = null;
        Node cur = root;

        while (cur != null) {
            if (key == cur.key) {
                throw new RuntimeException("key(" + key + ") 已经重复了");
            } else if (key < cur.key) {
                parent = cur;
                cur = cur.left;
            } else {
                parent = cur;
                cur = cur.right;
            }
        }

        // 直到找到 null 的位置，才真正开始插入
        if (key < parent.key) {
            cur = parent.left = new Node(key, parent);
        } else {
            // 这里只能是 key > parent.key，因为如果相等
            // 刚才循环中就抛异常了
            cur = parent.right = new Node(key, parent);
        }

        // 上面的过程是，正常搜索树的插入过程
        // parent 是要调整 BF 的结点
        // cur 是破坏源所在的根结点
        while (true) {
            // 根据情况，更新平衡因子
            if (cur == parent.left) {
                parent.bf++;
            } else {
                // cur == parent.right
                parent.bf--;
            }

            // 分情况处理
            if (parent.bf == 0) {
                break;
            } else if (parent.bf == 2) {
                // 进行失衡的修复
                // 左左失衡 OR 左右失衡
                if (cur.bf == 1) {
                    // 左左失衡
                    fixLeftLeftLoseBalance(parent);
                } else {
                    // -1
                    // 左右失衡
                    fixLeftRightLoseBalance(parent);
                }
                break;
            } else if (parent.bf == -2) {
                // 进行失衡的修复
                // 右右失衡 OR 右左失衡
                if (cur.bf == -1) {
                    // 右右失衡
                    fixRightRightLoseBalance(parent);
                } else {
                    // 1
                    // 右左失衡
                    fixRightLeftLoseBalance(parent);
                }
                break;
            } else if (parent == root){
                // -1/1 已经到根的位置了
                break;
            }

            // 如果需要继续（parent.bf==1/-1）
            Node parentOfParent = parent.parent;
            cur = parent;
            parent = parentOfParent;
        }
    }
    
    //左旋
    private void leftRotate(Node parent) {
        // 如果前面实现都正确，并且已经走到这个位置时，说明 parent 一定不是 null
        // 并且 parent.right 也一定不是 null
        Node parentOfParent = parent.parent;
        Node right = parent.right;
        Node leftOfRight = right.left;
        // parentOfParent 和 leftOfRight 可能是 null

        right.parent = parentOfParent;
        // 需要明确越来 parent 是 parentOfParent 的左还是右
        if (parentOfParent == null) {
            // 原来的根是 parent
            // 现在的根是 right
            root = right;
        } else if (parent == parentOfParent.left) {
            parentOfParent.left = right;
        } else {
            parentOfParent.right = right;
        }

        right.left = parent;
        parent.parent = right;

        parent.right = leftOfRight;
        if (leftOfRight != null) {
            leftOfRight.parent = parent;
        }
    }

    //右旋
    private void rightRotate(Node parent) {
        Node parentOfParent = parent.parent;
        Node left = parent.left;
        Node rightOfLeft = left.right;

        left.parent = parentOfParent;
        if (parentOfParent == null) {
            root = left;
        } else if (parent == parentOfParent.left) {
            parentOfParent.left = left;
        } else {
            parentOfParent.right = left;
        }

        left.right = parent;
        parent.parent = left;

        parent.left = rightOfLeft;
        if (rightOfLeft != null) {
            rightOfLeft.parent = parent;
        }
    }

    private void fixRightLeftLoseBalance(Node parent) {
        Node rightOfNode = parent.right;
        Node leftOfRightOfNode = rightOfNode.left;

        rightRotate(rightOfNode);
        leftRotate(parent);

        if (leftOfRightOfNode.bf == -1) {
            parent.bf = 1;
            rightOfNode.bf = leftOfRightOfNode.bf = 0;
        } else if (leftOfRightOfNode.bf == 1) {
            rightOfNode.bf = -1;
            parent.bf = leftOfRightOfNode.bf = 0;
        } else {
            parent.bf = rightOfNode.bf = leftOfRightOfNode.bf = 0;
        }
    }

    private void fixRightRightLoseBalance(Node parent) {
        Node rightOfNode = parent.right;

        leftRotate(parent);

        parent.bf = rightOfNode.bf = 0;
    }

    private void fixLeftRightLoseBalance(Node parent) {
        // 没必要进行 null 比较，已经走到这里来，如果外面的方法实现没问题，肯定不是出现 null
        Node leftOfNode = parent.left;
        Node rightOfLeftOfNode = leftOfNode.right;

        leftRotate(leftOfNode);//左旋
        rightRotate(parent);//右旋

        // 根据之前的计算结果，填写 BF 即可
        if (rightOfLeftOfNode.bf == 1) {
            parent.bf = -1;
            leftOfNode.bf = 0;
            rightOfLeftOfNode.bf = 0;
        } else if (rightOfLeftOfNode.bf == -1) {
            parent.bf = 0;
            leftOfNode.bf = 1;
            rightOfLeftOfNode.bf = 0;
        } else {
            parent.bf = leftOfNode.bf = rightOfLeftOfNode.bf = 0;
        }
    }

    private void fixLeftLeftLoseBalance(Node parent) {
        Node leftOfNode = parent.left;

        // 左左失衡，对失衡结点右旋
        rightRotate(parent);

        // 根据计算的结果，更新 BF
        parent.bf = leftOfNode.bf = 0;
    }

    /**
     * 在 AVL 树中查找对应的 key
     * @param key 要查找的关键字
     * @return AVL 是否包含这个 key
     */
    public boolean contains(int key) {
        Node cur = root;

        while (cur != null) {
            if (key == cur.key) {
                return true;
            } else if (key < cur.key) {
                cur = cur.left;
            } else {
                cur = cur.right;
            }
        }

        return false;
    }

    public void verify() {
        List<Integer> inOrderList = new ArrayList<>();
        // 计算该数的中序遍历
        inOrder(inOrderList, root);
        // 如何判断其是否有序呢？  把得到中序序列排序，如果排序后的结果和原来的结果一样，说明原来就有序
        List<Integer> inOrderListCopy = new ArrayList<>(inOrderList);
        Collections.sort(inOrderListCopy);

        if (!inOrderListCopy.equals(inOrderList)) {
            throw new RuntimeException("AVL 树规则不满足：中序遍历无序");
        }
        System.out.println("中序有序：验证OK");

        // 验证每个结点的 BF 是否计算正确
        preOrderAndCalcBF(root);
        System.out.println("BF 计算正确性: 验证OK");

        // 验证每个结点的 BF 是否都是 (-1, 0, 1)
        preOrderAndVerifyBF(root);
        System.out.println("BF 满足AVL特性: 验证OK");
    }

    private static void preOrderAndVerifyBF(Node node) {
        if (node != null) {
            if (node.bf != -1 && node.bf != 0 && node.bf != 1) {
                throw new RuntimeException("结点(" + node.key + ")的 BF 是 " + node.bf);
            }

            preOrderAndVerifyBF(node.left);
            preOrderAndVerifyBF(node.right);
        }
    }

    private static int height(Node node) {
        if (node == null) {
            return 0;
        }

        int left = height(node.left);
        int right = height(node.right);
        return Math.max(left, right) + 1;
    }

    private static void preOrderAndCalcBF(Node node) {
        if (node != null) {
            int left = height(node.left);
            int right = height(node.right);
            if (left - right != node.bf) {
                throw new RuntimeException("结点(" + node.key + ")的 BF 计算有错误");
            }

            preOrderAndCalcBF(node.left);
            preOrderAndCalcBF(node.right);
        }
    }

    private static void inOrder(List<Integer> list, Node node) {
        if (node != null) {
            inOrder(list, node.left);
            // 处理 node
            list.add(node.key);
            inOrder(list, node.right);
        }
    }
}

(3) Main.java

import java.util.Random;

public class Main {
    public static void main(String[] args) {
        Random random = new Random(20200705);
        AVLTree tree = new AVLTree();

        for (int i = 0; i < 1000; i++) {
            int r = random.nextInt(10000);
            try {
                tree.insert(r);
            } catch (RuntimeException e) {
                System.out.println(e.getMessage());
            }
        }
        tree.verify();
    }
}

长不大的大灰狼

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
常用的查找算法简介以及AVL树

平衡二叉搜索树——AVL树——平衡二叉搜索树（Self-balancing binary search tree）Ⅰ 搜索/查找——相关的算法及数据结构（1）遍历查找比较方式：equals()时间复杂度：O(n)（2）二分查找比较方式：compare()时间复杂度：O(log n)对数据要求强约束：必须是数组数据必须有序二分查找是基于比较的查找（小于中间值的往左边找，大于中间值的往右边找），只适合于静态数据（数据不会发生变化），因为插入或者删除可能会破坏数组的有序性，而为了维护约
复制链接

扫一扫