AVL树的实现

AVL树的概念：

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

1.它的左右子树都是AVL树

2.左子树和右子树高度之差（简称平衡因子）的绝对值不超过（-1,0,1）

如果一棵二叉搜索树是高度平衡的，它就是AVL树，如果它有n个结点，其高度可保持在O（lgn）,平均搜索时间复杂度O（lg(n)）。AVL在构建时，插入的每一个节点都需要满足搜索二叉树的性质，但同时也要保证左右子树的高度之差的绝对值不超过1，则AVL在构建时需要做平衡化旋转。

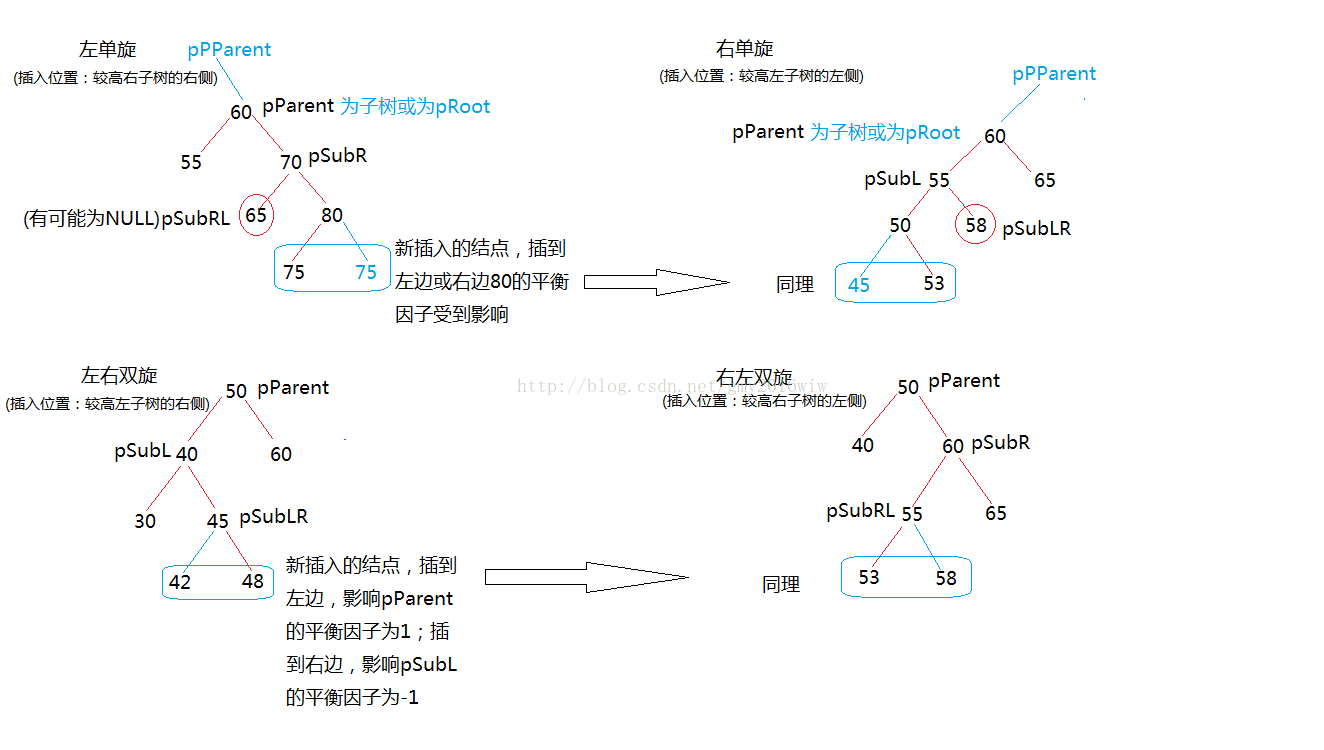
平衡化旋转：如果在一棵原本是平衡的二叉搜索树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，使之平衡化。如下图，是四种平衡化旋转的情况：

下面我们来看代码的实现：

#include<iostream>
using namespace std;

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode(const K& key, const V& value)
	:_key(key)
	, _value(value)
	, _pleft(NULL)
	, _pright(NULL)
	, _pParent(NULL)
	, _bf(0)
	{}

	AVLTreeNode<K, V>* _pleft;
	AVLTreeNode<K, V>* _pright;
	AVLTreeNode<K, V>* _pParent;
	K _key;
	V _value;
	int _bf;
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	AVLTree()
		:_pRoot(NULL)
	{}

	~AVLTree()
	{}

	bool Insert(const K& key, const V& value)
	{
		return _Insert(key, value);
	}

	void InOrder()
	{
		_InOrder(_pRoot);
		cout << endl;
	}

	size_t Height()
	{
		return _Height(_pRoot);
	}

	bool IsBalanceTree()
	{
		return IsBalanceTree(_pRoot);
	}

	bool Remove(const K& key)
	{
		return _Remove(key,_pRoot);
	}

	Node* firstInOrder(Node*& node)
	{
		return _firstInOrder(node);
	}

protected:
	bool _Insert(const K& key, const V& value)
	{
		if (_pRoot == NULL)
		{
			_pRoot = new Node(key, value);
			return true;
		}
		Node* pCur = _pRoot;
		Node* pParent = NULL;
		while (pCur)
		{
			if (key < pCur->_key)
			{
				pParent = pCur;
				pCur = pCur->_pleft;
			}
			else if (key > pCur->_key)
			{
				pParent = pCur;
				pCur = pCur->_pright;
			}
			else
			{
				return false;
			}
		}
		pCur = new Node(key, value);
		if (key < pParent->_key)
		{
			pParent->_pleft = pCur;
			pCur->_pParent = pParent;
		}
		else
		{
			pParent->_pright = pCur;
			pCur->_pParent= pParent;
		}
		while (pParent)
		{
			if (pParent->_pright == pCur)
				pParent->_bf++;
			else
				pParent->_bf--;
			if (pParent->_bf == 1 || pParent->_bf == -1)
			{
				pCur = pParent;
				pParent = pCur->_pParent;
			}
			else if (pParent->_bf == 0)
			{
				break;
			}
			else
			{
				if (pParent->_bf == 2)
				{
					Node* pSubR = pParent->_pright;
					if (pSubR->_bf == 1)
						_RotateL(pParent);
					else
						_RotateRL(pParent);
				}
				else
				{
					Node* pSubL = pParent->_pleft;
					if (pSubL->_bf == -1)
						_RotateR(pParent);
					else
					{

						_RotateLR(pParent);
					}
				}
				break;
			}
		}
		return true;
	}

	void _RotateL(Node*& pParent)
	{
		Node* pSubR = pParent->_pright;
		Node* pSubRL = pSubR->_pleft;
		pParent->_pright = pSubRL;
		if (pSubRL)
		{
			pSubRL->_pParent = pParent;
		}
		pSubR->_pleft = pParent;
		Node* pPParent = pParent->_pParent;
		pParent->_pParent = pSubR;
		if (NULL == pPParent)
			_pRoot = pSubR;
		else
		{
			if (pPParent->_pleft == pParent)
				pPParent->_pleft = pSubR;
			else
				pPParent->_pright = pSubR;
		}
		pSubR->_pParent = pPParent;
		pParent->_bf = pSubR->_bf = 0;
	}

	void _RotateR(Node*& pParent)
	{
		Node* pSubL = pParent->_pleft;
		Node* pSubLR = pSubL->_pright;
		pParent->_pleft = pSubLR;
		if (pSubLR)
		{
			pParent->_pright = pSubLR;
		}
		pSubL->_pright = pParent;
		Node* pPParent = pParent->_pParent;
		pParent->_pParent = pSubL;
		if (NULL == pPParent)
			_pRoot = pSubL;
		else
		{
			if (pPParent->_pleft == pParent)
				pPParent->_pleft = pSubL;
			else
				pPParent->_pright = pSubL;
		}
		pSubL->_pParent = pPParent;
		pParent->_bf = pSubL->_bf = 0;
	}
	
	void _RotateLR(Node* pParent)
	{
		Node* pSubL = pParent->_pleft;
		Node* pSubLR = pSubL->_pright;
		int bf = pSubL->_pright->_bf;
		_RotateL(pParent->_pleft);
		_RotateR(pParent);

		//if (pParent->_pright)
		//{
			if (bf == -1)
			{
				pParent->_bf = 1;
				pSubL->_bf = 0;
			}
			else if (bf == 1)
			{
				pParent->_bf = 0;
				pSubL->_bf = -1;
			}
			else
			{
				pParent->_bf = 0;
				pSubL->_bf = 0;
			}
		//}
	}

	void _RotateRL(Node* pParent)
	{
		Node* pSubR = pParent->_pright;
		Node* pSubRL = pSubR->_pleft;
		int bf = pSubR->_pleft->_bf;
		_RotateR(pParent->_pright);
		_RotateL(pParent);

		//if (pParent->_pleft)
		//{
			if (bf == 1)
			{
				pParent->_bf = -1;
				pSubR->_bf = 0;
			}
			else if (bf==-1)
			{
				pParent->_bf = 0;
				pSubR->_bf = 1;
			}
			else
			{
				pParent->_bf = 0;
				pSubR->_bf = 0;
			}

		//}
	}

	void _InOrder(Node* pRoot)
	{
		if (pRoot)
		{
			_InOrder(pRoot->_pleft);
			cout << pRoot->_key << " ";
			_InOrder(pRoot->_pright);
		}
	}

	size_t _Height(Node* pRoot)
	{
		if (NULL == pRoot)
			return 0;
		if (NULL == pRoot->_pleft&&NULL == pRoot->_pright)
			return 1;
		size_t LeftHeight = _Height(pRoot->_pleft);
		size_t RightHeight = _Height(pRoot->_pright);
		return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
	}

	bool _IsBalanceTree(Node* pRoot)
	{
		if (NULL == pRoot)
			return true;
		int LeftHeight = _Height(pRoot->_pleft);
		int RightHeight = _Height(pRoot->_pright);
		if (pRoot->_bf != RightHeight - LeftHeight || abs(pRoot->_bf) > 1)
			return false;
		return _IsBalanceTree(pRoot->_pleft) && _IsBalanceTree(pRoot->_pright);
	}

	bool _Remove(const K& key, Node* pRoot)
	{
		if (pRoot == NULL)
			return true;
		Node* pParent = NULL;
		Node* pCur = pRoot;
		while (pCur)
		{
			if (key < pCur->_key)
			{
				pParent = pCur;
				pCur = pCur->_pleft;
			}
			else if (key>pCur->_key)
			{
				pParent = pCur;
				pCur = pCur->_pright;
			}
			else
			{
				return false;
			}
		}
		Node* firstnode = NULL;
		if (pCur->_pleft && pCur->_pright)
		{
			firstnode = _firstInOrder(pCur);
			pCur = firstnode;
			firstnode->_pParent = pParent;
			delete pCur;
			pCur = NULL;
		}
	    if(pCur->_pleft != NULL&&pCur->_pright == NULL)
		{
			pCur->_pleft = firstnode;
			firstnode->_pParent = pParent;
			delete pCur;
			pCur = NULL;
		}
		if (pCur->_pleft == NULL&&pCur->_pright != NULL)
		{
			pCur->_pright = firstnode;
			firstnode->_pParent = pParent;
			delete pCur;
			pCur = NULL;
		}
		if (pCur->_pleft == NULL&&pCur->_pright == NULL)
		{
			delete pCur;
			pCur = NULL;
		}

		//判断pCur是pParent的左孩子还是右孩子
		while (pParent)
		{
			if (firstnode == pParent->_pleft)
				pParent->_bf++;
			else
				pParent->_bf--;
			if (pParent->_bf == 1 || pParent->_bf == -1)
				return true;
			else if (pParent->_bf == 0)
			{
				firstnode = pParent;
				pParent = pParent->_pParent;
			}
			else
			{
				if (pParent->_bf == 2)
				{
					if (firstnode->_bf == 1)
						_RotateL(pParent);
					else
						_RotateRL(pParent);
				}
				else
				{
					if (firstnode->_bf == -1)
						_RotateR(pParent);
					else
						_RotateLR(pParent);
				}
				break;
			}
		}
		return true;
	}

	Node* _firstInOrder(Node*& node)
	{
		while (node->_pleft)
		{
			node = node->_pleft;
		}
		return node;
	}
private:
	Node* _pRoot;
};