1、中心极限定理 (Central Limit Theorem)
1)中心极限定理(就是描述样本均值的分布情况)
随着样本容量(Sample size) n趋于无穷,
- 样本均值(Sampling Distribution of the Sample Mean)的分布越接近正态分布
- 样本均值的标准差(Standard Error of the Mean) 变小:偏度(Skew)更接近于0,峰度(Kurtosis)也更接近于0
- 这里样本均值指的是选取多个样本,每个样本可以求出一个样本均值,多个样本均值的分布符合正态分布

-
大数定律 Law of Large Number:随着样本容量n越大,样本均值越接近总体均值
-
除了样本均值,样本众数、样本和,样本极差等统计量也适用
-
一般n>30即可看作样本均值为正态分布
2)样本均值的抽样分布
样本均值的标准差(Standard Error of the Mean)
σ
x
‾
=
σ
n
\sigma_{\overline{x}}=\frac{\sigma}{\sqrt{n}}
σx=nσ
偏度 (Skew)

峰度(Kurtosis)

3)利用标准正态分布求概率的方法
- 确定分布(均值 μ \mu μ和标准差 σ \sigma σ)与范围
- 标准化,使其均值为0,标准差为1,得出标准正态变量Z, Z ∼ N ( 0 , 1 ) Z\sim N\left(0,1\right) Z∼N(0,1)
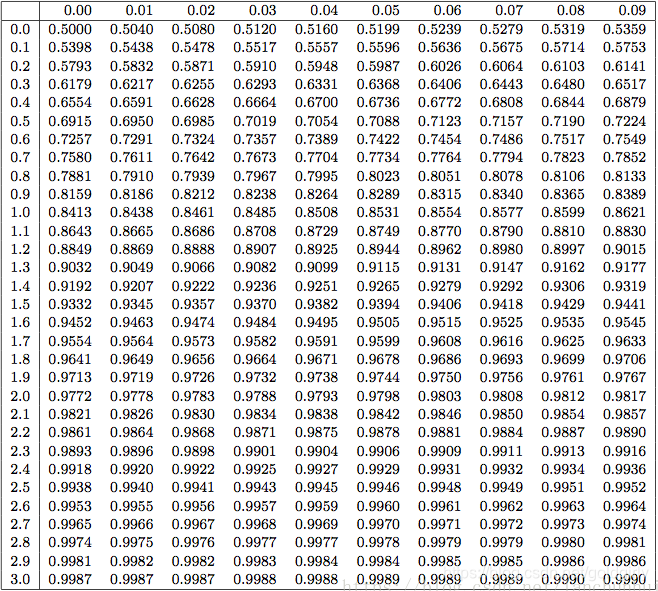
- 查概率表
标准化是为了使其对应查找标准正态分布概率表
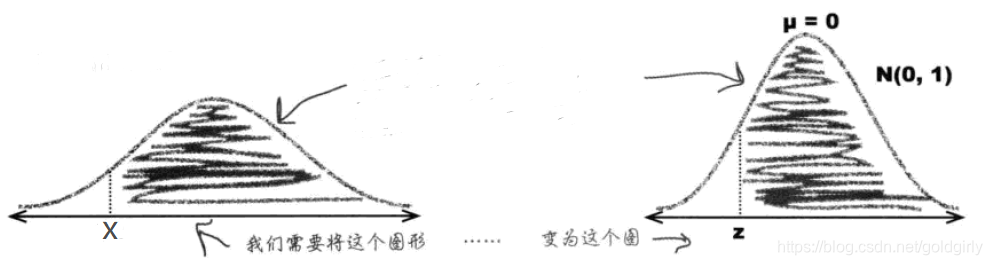


4)实例
(1)男性在户外活动时平均喝2L水(标准差是0.7L)。50人全天户外旅行,准备110L水.这些水不够的概率是多少?
- 确定分布
-
50个人看作样本,样本容量 n = 50 n=50 n=50
-
50人准备110L水,即平均喝水 x ‾ = 110 / 50 = 2.2 L \overline{x}=110/50=2.2L x=110/50=2.2L,均值分布服从正态分布
-
求水不够的概率,等价于求平均喝水超过2.2L的概率 P ( x ‾ > 2.2 ) = ? P\left(\overline{x}>2.2\right)=? P(x>2.2)=?
-
样本均值抽样分布的标准差 σ x ‾ = σ n ≈ 0.099 \sigma_{\overline{x}}=\frac{\sigma}{\sqrt{n}}\approx0.099 σx=nσ≈0.099
- 标准化
z = x ‾ − μ σ = 2.2 − 2 0.099 ≈ 2.02 z=\frac{\overline{x}-\mu}{\sigma}=\frac{2.2-2}{0.099}\approx 2.02 z=σx−μ=0.0992.2−2≈2.02 - 查概率表
查表可知 P ( Z > 2.02 ) = 1 − 0.9783 = 0.0217 P\left(Z>2.02\right)=1-0.9783=0.0217 P(Z>2.02)=1−0.9783=0.0217

2、参数估计:点估计
x
‾
:
样
本
均
值
μ
:
总
体
均
值
μ
^
:
总
体
均
值
的
点
估
计
\overline{x}:样本均值\\ \mu:总体均值\\\hat\mu:总体均值的点估计
x:样本均值μ:总体均值μ^:总体均值的点估计
均值的点估计::
μ
^
=
x
‾
\hat\mu=\overline{x}
μ^=x

S
2
:
样
本
方
差
σ
2
:
总
体
方
差
σ
^
2
:
总
体
方
差
的
点
估
计
S^2:样本方差\\\sigma^2:总体方差\\\hat\sigma^2:总体方差的点估计
S2:样本方差σ2:总体方差σ^2:总体方差的点估计
方差的点估计(用样本数据估计总体方差):
σ
^
2
=
S
2
=
∑
(
x
−
x
‾
)
2
n
−
1
\hat\sigma^2=S^2=\frac{\sum_({x-\overline{x}})^2}{n-1}
σ^2=S2=n−1∑(x−x)2
2) 区间估计
其实就是求置信区间 见下
3、参数估计:区间估计——求置信区间
1)置信区间是什么?
在样本估计总体均值时,我们需要知道估计的准确度,因此选定一个区间[a,b],目的是让这个区间包含总体均值,这个区间叫做置信区间。
对于这个区间有多大概率包含总体均值,这个概率称为置信水平,是我们对这个范围的可信程度。。置信水平是根据实际问题自己确定的,一般设定为95%即两个标准差。
2)怎么计算置信区间?(结合例子更具体的讲解可以看深入浅出统计学)
解题的时候要区分清楚哪些是样本统计量(已知),哪些是总体统计量(未知,通过点估计得出)
- 选择总体统计量
即确定你要求的那个总体均值 μ \mu μ - 求样本均值的抽样分布
1)计算样本均值 x ‾ \overline{x} x
2)计算样本均值标准差 σ x ‾ = σ n ≈ S n \sigma_{\overline{x}}=\frac{\sigma}{\sqrt n}\approx \frac{S}{\sqrt n} σx=nσ≈nS
(由于事先我们并不知道总体的标准差。因此要用样本方差作为总体方差的估计(点估计),需注意是会跟随样本的变化而变化。)
3)得出样本均值的分布: X ‾ ∼ N ( x ‾ , σ x ‾ ) \overline{X}\sim N\left(\overline{x},\sigma_{\overline{x}}\right) X∼N(x,σx),因为这里就是通过样本均值估计总体均值的区间,所以把 x ‾ \overline{x} x换成 μ \mu μ, X ‾ ∼ N ( μ , σ x ‾ ) \overline{X}\sim N\left(\mu,\sigma_{\overline{x}}\right) X∼N(μ,σx) - 确定置信水平
- 求出置信上下限
1)当样本容量较大(>30)时,查找z表格;
a. 标准化
即把 X ‾ ∼ N ( μ , σ x ‾ ) \overline{X}\sim N\left(\mu,\sigma_{\overline{x}}\right) X∼N(μ,σx)转换成标准正态分布 Z ‾ ∼ N ( 0 , 1 ) \overline{Z}\sim N\left(0,1\right) Z∼N(0,1),Z就是标准化后的 X ‾ \overline{X} X Z = x ‾ − μ σ x ‾ Z=\frac{\overline{x}-\mu}{\sigma_{\overline{x}}} Z=σxx−μ
b. 用 μ \mu μ改写不等式
(以置信水平为95%为例)
P ( − 1.96 < Z < 1.96 ) = 0.95 P ( − 1.96 < x ‾ − μ σ x ‾ < 1.96 ) = 0.95 P(-1.96<Z<1.96)=0.95\\P(-1.96<\frac{\overline{x}-\mu}{\sigma_{\overline{x}}}<1.96)=0.95 P(−1.96<Z<1.96)=0.95P(−1.96<σxx−μ<1.96)=0.95
其中 x ‾ 、 σ x ‾ \overline{x}、\sigma_{\overline{x}} x、σx已知,带入求出 a < μ < b a<\mu<b a<μ<b即可得出置信区间(a,b)
置信区间简便算法,用下面的表可以取代第4步,直接带入求出
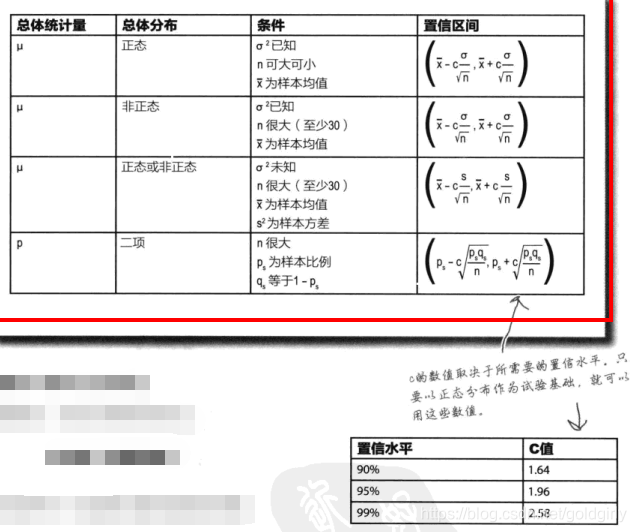
2)当样本容量较小(<30)时,为t分布,确定自由度(degrees of freedom) t=n-1,查找t分布表(跟正态分布的计算差别只在查表,其他都相同)

3)实例
(1) 某地区教学区获得一批技术拨款,用于在教师中安排4台一组的计算机.该区总共有6250名教师,随机抽取250名,并且问他们是否认为计算机是教师必备的教学工具.抽取的教师中,有142名认为计算机是教学必备的工具.
问题1:
计算一个99%置信区间,其中教师认为计算机是必备的教学工具.
定义:
1表示计算机被认为是必备工具,占比为p,
0表示计算机被认为不是必备工具,占比为q=1-p.

z表格的值应该为0.99/2+0.5=0.995
对应2.58个标准差处
0.568
±
2.58
×
0.031
=
0.568
±
0.08
0.568\pm2.58\times0.031 = 0.568\pm0.08
0.568±2.58×0.031=0.568±0.08
即
0.488
∼
0.648
=
48.8
%
∼
64.8
%
0.488\sim0.648=48.8\%\sim64.8\%
0.488∼0.648=48.8%∼64.8%
有99%的几率,48.8%~64.8%的老师认为计算机是必备的
问题2:
保持99%置信水平的前提下,如何缩小置信区间?
抽取更大的样本.
(2) 小样本容量置信区间
7个患者在服用新药3个月后测量血压.其血压上升值分别为1.5, 2.9, 0.9, 3.9, 3.2, 2.1, 1.9.为总体中所有病人的血压升高真正期望值建立一个95%的置信区间。

这里样本容量太小了,不能认为其样本均值为正态分布,不能使用中心极限理论。可以认为是t分布,查t分布表


即
1.38
∼
3.3
1.38\sim3.3
1.38∼3.3

参考资料:
可汗学院统计学:https://www.bilibili.com/video/av7199273/?p=73
简客:https://jentchang.github.io/contents/math/statistical.html
《深入浅出统计学》

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








