【机器学习入门一】决策树及ID3决策树的python实现

最新推荐文章于 2022-06-23 18:43:29 发布

「已注销」

最新推荐文章于 2022-06-23 18:43:29 发布

阅读量659

点赞数 2

分类专栏：机器学习入门

本文链接：https://blog.csdn.net/gongyi_yf/article/details/79511095

版权

本文介绍了ID3决策树的基本流程、划分选择（信息增益、增益率、基尼指数）、剪枝处理（预剪枝、后剪枝）、连续值与缺失值处理，并提供了Python代码实现。通过西瓜挑选的例子阐述了决策树的工作原理，探讨了如何避免过拟合和处理连续及缺失值的情况。

摘要由CSDN通过智能技术生成

本文实现的是ID3决策树。一开始是想实现一下adaboost算法，但是弱分类器选择的是决策树桩，因此干脆先实现决策树。本文基于周志华老师的《机器学习》第四章

正文

1. 基本流程

决策树对某个样本进行分类实际上是模拟人们思维的一种决策过程。以买西瓜为例，人们在挑选西瓜时的决策过程大致为如下过程，首先看一看西瓜的色泽，如果是青绿的，那么这个瓜可能是好瓜，如果这个瓜外表已经泛黄甚至是黑的，就几乎可以判定这个瓜不好吃。是不是颜色是青绿的一定是好瓜呢？显然也未必，人们还要继续看看其他的一些属性，比如根蒂，根据经验，如果根蒂是硬挺的，说明瓜可能刚采摘不久，还比较新鲜，如果是蜷缩柔软的，说明已经摘下很长时间了。那么根据我们的经验，可能根蒂硬挺的瓜是好瓜。这样继续判断别的属性，直到我们可以断定这个瓜是好瓜还是坏瓜为止。
这个决策过程可以用如下的决策流程图来表示：

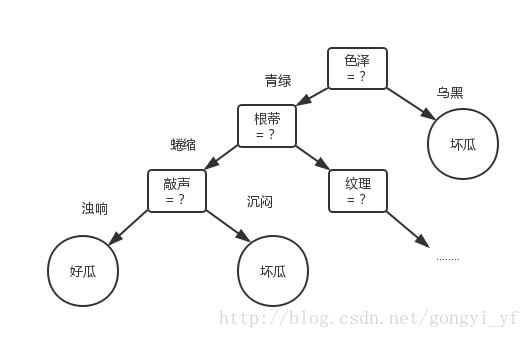
这是西瓜问题的一种可能的决策过程。这个树形的结构就是所说的决策树。特殊一点，我在买瓜的时候没有什么经验，看着别人买瓜的时候听一听瓜的敲声，我也会装作很懂的敲一敲，最后挑个长的好看的。那么显然此时我的决策树只有一层，就叫做决策树桩。
决策树的生成过程大致如下：首先选择一个“好的属性”，根据该属性的所有取值为这个节点生成孩子节点，如上图中的色泽属性有“青绿”和“乌黑”2种可能的取值，于是色泽节点就有两个孩子节点，将所有色泽为“青绿”的样本划入第一个节点，所有色泽为“乌黑”的样本划入第二个节点。这样递归生成决策树。
这里有两个问题：（1）什么时候递归返回？（2）什么是“好的属性”？
首先看第一个问题。递归返回一个有3种情况，（1）当前节点包含的样本全部属于一个类别。（2）当前已经使用了样本的所有属性，或者样本在所有属性上的取值相同，无法区分。（3）当前节点包含的样本集合为空，不能划分。
第一种情况下，叶节点的类别就是这些样本的类别。第二种情况下，叶节点的类别是样本集中所属样本数量最多的类别。第三种情况下，取父节点中所含样本最多的类别。
这是第一个问题，那么什么是“好的属性”呢？

2. 划分选择

2.1 信息增益

直观上来看，我们在做出决策时，希望当前选择的属性能够把尽可能多的样本分对，即按照每个取值，子样本集的“纯度”尽可能高。在信息学上，经常用信息熵来度量集合的纯度。
假定当前样本集合 D中第 $\kappa$ 类样本中所占的比例为 $p_{\kappa}\quad (\kappa = 1,2,3,\ldots,\mid\gamma\mid)$ ，则D的信息熵定义为：

E n t (D) = - \sum k = 1 ∣ γ ∣ p k l o g 2 p k (1)

$Ent(D)=-\sum_{k=1}^{\mid \gamma \mid}p_k log_2p_k\quad\quad\quad(1)$
Ent(D)的值越小，则D的纯度越高。
假定离散属性a有V可能的取值

{ a1,a2,…,aV} { a 1 , a 2 , … , a V } $\{a^1,a^2,\ldots,a^V\}$ ，若使用a来对样本集合D进行划分，则会产生V个分枝节点，其中第

ν ν $\nu$ 个分枝节点包含了D中所有在属性a上取值为

aν a ν $a^{\nu}$ 的样本，记为

Dν D ν $D^{\nu}$ 。根据式(1)计算出

Dν D ν $D^{\nu}$ 的信息熵，再考虑到不同的分枝节点所包含的样本数不同，给分枝节点赋予权重

∣Dν∣/∣D∣ ∣ D ν ∣ / ∣ D ∣ ${\mid D^{\nu}\mid / \mid D\mid}$ ，即样本数越多的分支节点的影响越大，于是可以计算出属性a对样本集D记性划分所获得的“信息增益”：

G a i n (D, a) = E n t (D) - \sum v = 1 V ∣ D ν ∣ ∣ D ∣ E n t (D ν) (2)

$Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{\mid D^{\nu}\mid}{\mid D\mid}Ent(D^{\nu})\quad\quad\quad(2)$
一般而言，信息增益越大，则意味着使用属性a来进行划分所获得的“纯度提升”越大，也可以理解为在划分的过程中获取的信息越多。因此，我们就优先选择使得