本文介绍如何对离散点进行求导。
对于一个点的值(函数上)我们可以通过泰勒级数展开,对其进行近似:

解出来一阶导数:

主要,我们就是靠这个式子来计算多阶的导数,如果把二阶以后的项去掉,那么一阶导数就是:
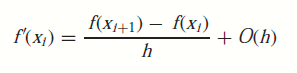
二阶导数就是:
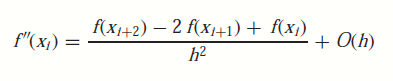
为了提高精度,我们可以留下更多的项数:比如留下二阶项:

简化后:

、总结一下:
向前微分公式:(forward)

向后微分公式:(backward)

中间微分:(centered)

本文介绍如何对离散点进行求导。
对于一个点的值(函数上)我们可以通过泰勒级数展开,对其进行近似:

解出来一阶导数:

主要,我们就是靠这个式子来计算多阶的导数,如果把二阶以后的项去掉,那么一阶导数就是:
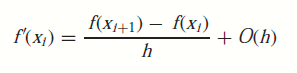
二阶导数就是:
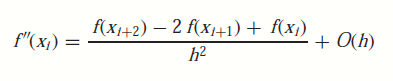
为了提高精度,我们可以留下更多的项数:比如留下二阶项:

简化后:

、总结一下:
向前微分公式:(forward)

向后微分公式:(backward)

中间微分:(centered)

 720
720

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


