【二叉树】用python实现AVL树

AVL树是平衡的二叉搜索树，其任意节点的平衡因子（左子树高度-右子树高度）始终为-1、0或1。AVL树的结构能够解决普通BTS由于有序插入导致的退化为链表的情况。

AVL树在二叉搜索树实现的基础上，主要在添加和删除节点时更新子树相关节点的平衡因子，同时对不平衡的子树进行旋转操作。其机制较为复杂，本文先介绍相关的背景知识，在做代码的实现。

1. 背景知识

1.1 节点平衡因子的调整顺序

与普通二叉搜索树不同的是：添加或删除节点后相关节点的平衡因子需做出调整。

• 添加操作

其基本规则包括：
（1）若该节点为左节点，则其父节点的平衡因子加1；若该节点为右节点，则其父节点的平衡因子减1；然后继续向上回溯父节点；
（2）若父节点的平衡因子调整为0，则说明以该父节点为根节点的子树达到了平衡，但高度不变，因此后续的祖先节点无需在做更新；
（3）若父节点的平衡因子仍为-1或1，则继续重复（1）；
（4）若父节点的平衡因子为-2或2，则以该父节点为根节点的子树进行旋转操作（具体细节见1.2），并调整旋转节点的平衡因子（具体细节见1.3）。旋转后的子树相较于原子树，高度不变，因此后续的祖先节点无需做更新；
（5）若有必要，一直回溯到AVL树的根节点为止。

显然，可以通过递归实现上述调整，其条件终止条件包括：
条件一：到达根节点；
条件二：某节点的平衡因子达到0；
条件三：某节点的平衡因子达到-2或2。

• 删除操作

删除操作是在原AVL树基础上任意删除某个节点的操作。根据普通二叉搜索树中删除操作的解读，无论删除的是根、中间还是叶子节点，其最终都可以转换为叶子节处的删除。

根据原AVL树的定义，若删除叶子节点所在最底层的子树原来是完全平衡的，则其父节点在删除后的平衡因子为1或-1，此时整棵子树的高度不变，因此无需继续上溯。

而若删除叶子节点所在最底层的子树原来并非是完全平衡的（即原父节点的平衡因子为1或-1），则删除后的平衡因子可能变为0、-2或2。若为0，则说明原子树父节点的平衡因子为1或-1；删除后子树的高度变化，因此需继续回溯。而对于-2和2，需要先采用左旋或右旋操作将子树平衡，然后视新的父节点的平衡因子选择继续回溯或者停止。

基于上面的分析，可采用类似于增加节点的递归操作实现调整，其条件终止条件包括：
条件一：到达根节点；
条件二：某节点的平衡因子达到-1或1。

1.2 子树的旋转

子树包括两种基本旋转方式：左旋和右旋。

• 左旋

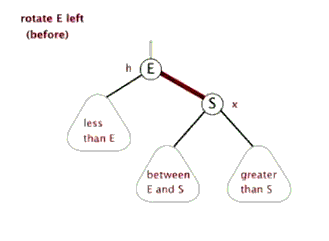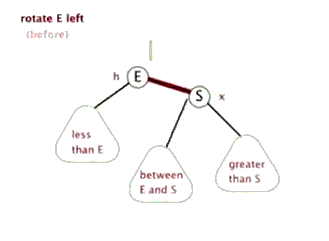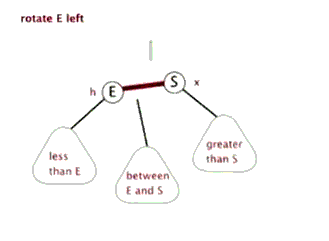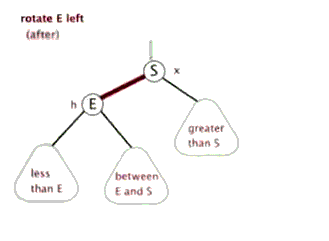
当右子树重（即根节点平衡因子为-2）时，需要进行左旋。其具体具体操作包括：
（1）根节点右孩子节点变为新的根节点，原根节点成为新根节点的左孩子节点；
（2）若原根节点本身就具有左孩子节点，则该节点成为原根节点的右孩子节点。

• 右旋

当左子树重（即根节点平衡因子为2）时，需要进行右旋。其具体具体操作包括：
（1）根节点左孩子节点变为新的根节点，原根节点成为新根节点的右孩子节点；
（2）若原根节点本身就具有右孩子节点，则该节点成为原根节点的左孩子节点。

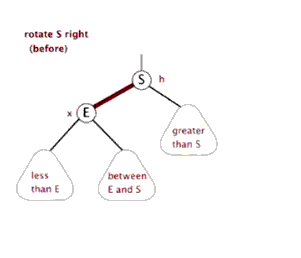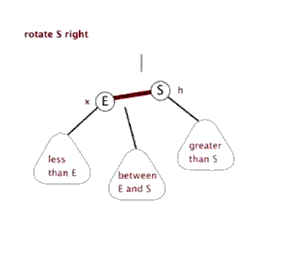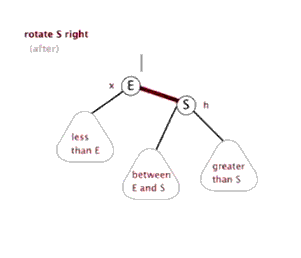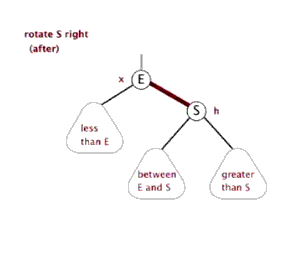
在删除节点后的再平衡过程中，由于原树已经处于平衡状态，叶子节点的删除（即使是非叶子节点，也会通过与后继节点的交换转换为叶子节点的删除）通过单次的左旋或右旋操作即可完成当前子树的再平衡。

而在添加节点后的再平衡过程中，情况会略显复杂，其可能涉及到双旋转的操作。具体而言，根据子树情况可分为四种变换：
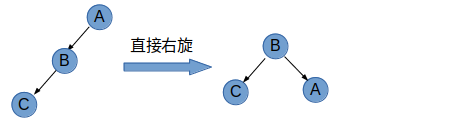
情况1： 根节点平衡因子小于0，右孩子节点的平衡因子也小于0，直接在对根节点所在的树进行左旋。

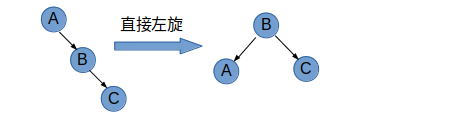
情况2：根节点平衡因子小于0，而右孩子节点的平衡因子大于0，先对右子树进行右旋，然后对根节点所在的树进行左旋。

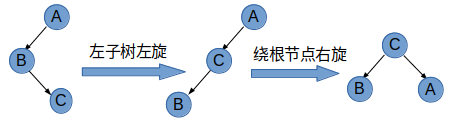
情况3： 根节点平衡因子大于0，左孩子节点的平衡因子也大于0，直接在对根节点所在的树进行右旋。

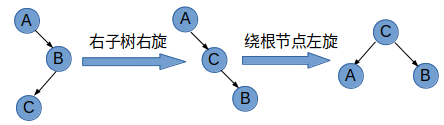
情况4： 根节点平衡因子大于0，而左孩子节点的平衡因子小于0，先对左子树进行左旋，然后对根节点所在的树进行右旋。

1.3 旋转后相关节点平衡因子的更新公式

值得注意的是：在每步的旋转过程中，只有发生位置变换的根节点和成为新的根节点的那个原孩子节点的平衡因子需要进行更新。而以其他节点为根节点的子树结构并未发生变动，因此节点上的平衡因子也无需变化。那么具体如何更新呢？我们可以推导下左旋和右旋下的更新公式。

• 左旋
  

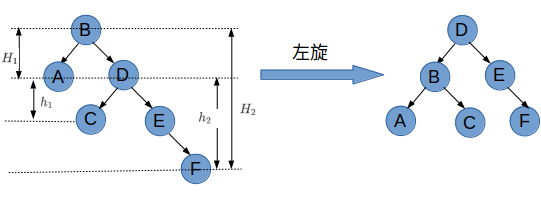
上图为一个典型的左旋示意图。我们不妨令旋转前，根节点（对应点B）的左、右子树高度分别为$H_1$和$H_2$；右孩子节点D（左旋后成为新根节点）为根节点的子树的左、右子树高度分别为$h_1$和$h_2$，则节点B和和节点D的平衡因子分别为：$$\begin{gathered} r_B=H_1-H_2 \\ {r}_D=h_1-h_2 \end{gathered}$$且满足$H_2=\max (h_1,h_2)+1$。

旋转后：点B的左子树不变，而右子树变成了点D的左子数，因此，其平衡因子变为：$$\begin{array}{rl}{\bar{r}}_B& =H_1-h_1\\ & =(H_1-H_2)+(H_2-h_1)\\ & =r_B+\max (0,h_2-h_1)+1\\ & \\ & \end{array}$$