全排列问题——浅谈递归

 

全排列问题——浅谈递归

 

最近对 COM的学习让我有些头晕眼花，于是打算做些轻松些的事情。

 

两年多以前我从第二家公司跳槽，有次去个地方面试，笔试的时候有这么道题目：给一个 <=9的自然数，打印出它的全排列，例如3，就打印123，132，213，231，312，321。题目看起来很容易，但其实不然，我当时是想了挺长时间的，可能后来面试官在外边等得有些不耐烦了，进来对我说：“这题目挺难的，想不出就算了。”我那时候快写出来了，于是就说：“再等等。”又过了大约10分钟，我认为我完成了，这道题目前后花了大约45分钟，当时没法上机，我无法验证我的答案是否正确，但我思路是肯定正确的。但后来公司没再给我消息，多半是那时候我涉世未深，经验不足，瞧我后面来的那位仁兄口若悬河，天花乱坠，有他这种老油条竞争应聘，我能成功就怪了。

 

这道题目适合用递归来做，适合用递归做的情况通常具备这两个条件： 1、大的操作可以拆分为小的操作，小的操作可以同样地拆分为更小的操作，直至原子操作；2、不确定一共需要拆分多少次。最经典的递归题目莫过于汉诺塔问题，C语言的教科书都喜欢用这题目作为例子，我这里就不多讲了。

 

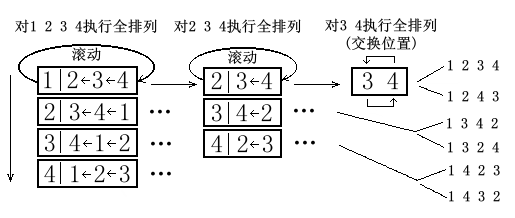
也许有的人奇怪，为什么题目限定这个给出的自然数小于等于 9？其实9的全排列已经挺恐怖了，因为总数就是9的阶乘：9!= 362880，那你以为 16的全排列一共有多少呢？16还不算一个大的数字吧，16!≈209228亿，如果你对这个数字还是没什么概念的话，那我告诉你，把16的全排列全部打印到文件并保存在磁盘上，那需要的磁盘空间是779435GB，嘿嘿，恐怕现在地球上还没有那么大的硬盘吧。所以题目限定了这个条件是很有意义的。用下面这幅图来说明我的算法：

图 1

排列函数拿到一个数组，就将这个数组第一个元素提取出来，把第二个元素到最后一个元素这一段作为一个新的数组，交给排列函数，然后滚动数组，把第二个元素提取出来，把刚才的第一个元素滚动到数组末尾，如图中的“ 2 3 4 1”，把“3 4 1”作为一个新的数组，交给排列函数，依次类推，直到滚动完成。可见这是个循环+递归的过程，循环是用于滚动数组的。

 

程序如下：

#define  MAX_NUM 9
int  g_arrNumber[MAX_NUM];  // to full arrangement
int  g_iTemp;  // for exchange
int  g_arrTemp[MAX_NUM];  // for exchange
void  PrintArray()
{
  for ( int  i = 0 ; i < MAX_NUM; i ++ )
 {
  printf( " %d  " , g_arrNumber[i]);
 }
 printf( " " );
}
// arr: the array to arrange
// iNum: the array's length
void  ArrangeNumber( int   * arr,  int  iNum)
{
  if  (iNum == 2 ) 
 {
   // print the result and exchange the two number in the array
  PrintArray();
  g_iTemp  =  arr[ 0 ];
  arr[ 0 ]  =  arr[ 1 ];
  arr[ 1 ]  =  g_iTemp;
   // print again and restore exchange the two number again
  PrintArray();
  g_iTemp  =  arr[ 0 ];
  arr[ 0 ]  =  arr[ 1 ];
  arr[ 1 ]  =  g_iTemp;
 }
  else   // iNum>2
 {
   // roll the array
   //  >---->---->---->---->
   //  2<---3<---4<---5<---1
   for ( int  i = 0 ; i < iNum; i ++ )
  {
   ArrangeNumber( & arr[ 1 ], iNum - 1 );
   g_iTemp  =  arr[ 0 ];
   memcpy(g_arrTemp,  & arr[ 1 ],  sizeof ( int ) * iNum - 1 );
   memcpy( & arr[ 0 ], g_arrTemp,  sizeof ( int ) * iNum - 1 );
   arr[iNum - 1 ]  =  g_iTemp;
  }
 }
}
int  _tmain( int  argc, TCHAR *  argv[], TCHAR *  envp[])
{
  // initialization
  for ( int  i = 0 ; i < MAX_NUM; i ++ )
  g_arrNumber[i]  =  i + 1 ;
  // full arrangement
 ArrangeNumber(g_arrNumber, MAX_NUM);
  return  nRetCode;
}

 

上周二我和原来公司的同事有次聚会，公司头说前阵子有场面试，他遇到一道题目，是二叉树的遍历，写一个程序遍历二叉树，把所有的叶子节点都打印出来，我问：“还有别的要求吗？”“没有了。”“那就用递归吧。”递归无疑提供了最简练的代码，考卷也会很清晰明了，何乐而不为。其实递归的效率非常低的，甚至觉得有些不负责任。如果遍历一棵简单的树也就罢了，如果树是系统盘的目录结构（很复杂），那执行效率肯定非常低下。为什么递归效率低下？因为递归函数会在运行时在栈区中复制大量程序代码，如果递归环节过多，甚至会导致一种“假死机”的现象，函数迟迟不能返回。所以说，能用循环就不用递归！当然考试喜欢考递归，我们要适应。 ^o^

 

那么如何把递归转换为迭代呢？我的做法通常是使用队列。 MFC的集合类模板中的CList就比较适合用来担当这个“队列”的容器，AddTail()往队列后面压入成员，GetHead()和RemoveHead()从队列前面取走成员，当然了，你可以自己写出更“专业”的队列容器，我喜欢偷懒而已。好，就拿遍历系统盘根目录为例：

 

int  _tmain( int  argc, TCHAR *  argv[], TCHAR *  envp[])
{
 CList < CString, CString  &>  queDirs;
  // add the system driver's root directory
 queDirs.AddTail(CString( " C: " ));
 WIN32_FIND_DATA stFind;
 CString csDirNow;
 CString csToFind;
 CString csToAdd;
 HANDLE hRtn;
  while  (queDirs.GetCount() > 0 ) 
 {
  csDirNow  =  queDirs.GetHead();
  queDirs.RemoveHead();
  csToFind  =  csDirNow  +   " /* " ;
  hRtn  =  FindFirstFile(csToFind.GetBuffer(csToFind.GetLength()),  & stFind);
  DWORD dwRtn  =  GetLastError();
   if (INVALID_HANDLE_VALUE  !=  hRtn)
  {
    // handle a directory
    if  (FILE_ATTRIBUTE_DIRECTORY == stFind.dwFileAttributes
     &&   0 != strcmp(stFind.cFileName, " . " ) 
     &&   0 != strcmp(stFind.cFileName,  " .. " ))
   {
    csToAdd.Format( " %s/%s " , csDirNow, stFind.cFileName);
    printf( " %s " , csToAdd.GetBuffer(csToAdd.GetLength()));
    queDirs.AddTail(csToAdd);
   }
   
    while (FindNextFile(hRtn,  & stFind))
   {
     // handle a directory
     if  (FILE_ATTRIBUTE_DIRECTORY == stFind.dwFileAttributes
      &&   0 != strcmp(stFind.cFileName, " . " )
      &&   0 != strcmp(stFind.cFileName,  " .. " ))
    {
     csToAdd.Format( " %s/%s " , csDirNow, stFind.cFileName);
     printf( " %s " , csToAdd.GetBuffer(csToAdd.GetLength()));
     
     queDirs.AddTail(csToAdd);
    }
   }
   FindClose(hRtn);
  }
 }
}

找到了一个有效目录，就把目录压入队列queDirs中去，然后一个一个从队列中取出目录，执行同样的分析，直到queDirs中没有内容为止，这样的迭代就不会出现递归所产生的这种情况：运行时代码在栈中的不可预测地大量复制。另外说明一下，程序使用了MFC，所以必须创建MFC工程方可，并且需要包含头文件afxtempl.h。

Jiang Guogang
20061204 于 上海浦东花木