from http://zh.wikipedia.org/wiki/%E7%9F%A9%E9%98%B5%E7%9A%84%E7%A7%A9
在线性代数中,一个矩阵A的列秩是A的线性无关的纵列的极大数目。类似地,行秩是A的线性无关的横行的极大数目。
矩阵的列秩和行秩总是相等的,因此它们可以简单地称作矩阵A的秩。通常表示为r(A),rk(A)或rank A。
m × n矩阵的秩最大为m和n中的较小者。有尽可能大的秩的矩阵被称为有满秩;类似的,否则矩阵是秩不足(或称为“欠秩”)的。
目录[隐藏] |
[编辑]可替代定义
[编辑]用向量组的秩定义
向量组的秩:在一个 m 维线性空间 E 中,一个向量组  的秩表示的是其生成的子空间的维度。考虑 m × n 矩阵
的秩表示的是其生成的子空间的维度。考虑 m × n 矩阵 ![A=[C_1,C_2, /cdots , C_n]](http://upload.wikimedia.org/math/7/f/3/7f3977c77d9a7c810bcddc20990f0f7b.png) ,将 A 的秩定义为向量组 F 的秩,则可以看到如此定义的 A 的秩就是矩阵 A 的线性无关列向量的极大数目,即 A 的列空间的维度(列空间是由A的纵列生成的Fm的子空间)。因为列秩和行秩是相等的,我们也可以定义A的秩为A的行空间的维度。
,将 A 的秩定义为向量组 F 的秩,则可以看到如此定义的 A 的秩就是矩阵 A 的线性无关列向量的极大数目,即 A 的列空间的维度(列空间是由A的纵列生成的Fm的子空间)。因为列秩和行秩是相等的,我们也可以定义A的秩为A的行空间的维度。
[编辑]用线性映射定义
考虑线性映射:
对于每个矩阵A,fA都是一个线性映射,同时,对每个 的 线性映射f,都存在矩阵A使得f = fA。也就是说,映射
的 线性映射f,都存在矩阵A使得f = fA。也就是说,映射
是一个同构映射。所以一个矩阵A的秩还可定义为fA的像的维度(像与核的讨论参见线性映射)。矩阵A称为fA的变换矩阵。这个定义的好处是适用于任何线性映射而不需要指定矩阵,因为每个线性映射有且仅有一个矩阵与其对应。秩还可以定义为n减f的核的维度;秩-零化度定理声称它等于 f的像的维度。
[编辑]性质
我们假定A是在域F上的m × n矩阵并描述了上述线性映射。
- 只有零矩阵有秩0
- A的秩最大为min(m,n)
- f是单射,当且仅当A有秩n(在这种情况下,我们称A有“满列秩”)。
- f是满射,当且仅当A有秩m(在这种情况下,我们称A有“满行秩”)。
- 在方块矩阵A (就是m = n)的情况下,则A是可逆的,当且仅当A有秩n(也就是A有满秩)。
- 如果B是任何n × k矩阵,则AB的秩最大为A的秩和B的秩的小者。
- 即:秩(AB)≤min(秩(A),秩(B))
- 推广到若干个矩阵的情况,就是:秩(A 1A 2...A m)≤min(秩(A 1),秩(A 2),...秩(A m))
-
证明:
- 考虑矩阵的秩的线性映射的定义,令A、B对应的线性映射分别为 f和 g,则AB表示复合映射 f·g,它的象 Im f·g是 g的像 Im g在映射 f作用下的象。然而 Im g是整个空间的一部分,因此它在映射 f作用下的象也是整个空间在映射 f作用下的象的一部分。也就是说映射 Im f·g是 Im f的一部分。对矩阵就是:秩(AB)≤秩(A)。
- 对于另一个不等式:秩(AB)≤秩(B),考虑 Im g的一组 基:(e 1,e 2,...,e n),容易证明(f(e 1),f(e 2),...,f(e n))生成了空间 Im f·g,于是 Im f·g的 维度小于等于 Im g的维度。对矩阵就是:秩(AB)≤秩(B)。
- 因此有:秩(AB)≤min(秩(A),秩(B))。若干个矩阵的情况证明类似。
-
作为"<"情况的一个例子,考虑积
-
- 两个因子都有秩1,而这个积有秩0。
- 可以看出,等号成立当且仅当其中一个矩阵(比如说 A)对应的线性映射不减少空间的维度,即是 单射,这时 A是满秩的。于是有以下性质:
-
- 如果B是秩n的n × k矩阵,则AB有同A一样的秩。
- 如果C是秩m的l × m矩阵,则CA有同A一样的秩。
- A的秩等于r,当且仅当存在一个可逆m × m矩阵X和一个可逆的n × n矩阵Y使得
[编辑]向量组的线性相关性
将m个n维列向量排列成 的矩阵A,这个对应矩阵的秩即为原向量组的秩。
的矩阵A,这个对应矩阵的秩即为原向量组的秩。
原向量组线性相关的充分必要条件为:
- r(A) < m
如果
- r(A) = m
则向量组线性无关。另外,不存在
- r(A) > m
特殊的,若向量的维数n大于向量的个数m,则根据:
这个向量组必然线性相关。
[编辑]计算
计算矩阵A的秩的最容易的方式是高斯消去法,即利用矩阵的初等变换生成一个行阶梯型矩阵,由于矩阵的初等变换不改变矩阵的秩,因此A的行梯阵形式有同A一样的秩。经过初等变换的矩阵的非零行的数目就是原矩阵的秩。
例如考虑4 × 4矩阵
我们看到第2纵列是第1纵列的两倍,而第4纵列等于第1和第3纵列的总和。第1和第3纵列是线性无关的,所以A的秩是2。这可以用高斯算法验证。它生成下列A的行梯阵形式:
它有两个非零的横行。
在应用在计算机上的浮点数的时候,基本高斯消去(LU分解)可能是不稳定的,应当使用秩启示(revealing)分解。一个有效的替代者是奇异值分解(SVD),但还有更少代价的选择,比如有支点(pivoting)的QR分解,它也比高斯消去在数值上更强壮。秩的数值判定要求对一个值比如来自SVD的一个奇异值是否为零的依据,实际选择依赖于矩阵和应用二者。
[编辑]应用
计算矩阵的秩的一个有用应用是计算线性方程组解的数目。如果系数矩阵的秩等于增广矩阵的秩,则方程组只要有一个解。在这种情况下,它有精确的一个解,如果它的秩等于方程的数目。如果增广矩阵的秩大于系数矩阵的秩,则通解有k个自由参量,这里的 k是在方程的数目和秩的差。否则方程组是不一致的。
在控制论中,矩阵的秩可以用来确定线性系统是否为可控制的,或可观察的。
[编辑]引用
- Horn, Roger A. and Johnson, Charles R. Matrix Analysis. Cambridge University Press, 1985. ISBN 0-521-38632-2.
- Kaw, Autar K. Two Chapters from the book Introduction to Matrix Algebra: 1. Vectors [1] and System of Equations [2]
[编辑]参见











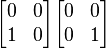



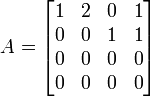














 749
749

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








